微分方程基础

<script src="http://widgets.amung.us/classic.js" type="text/javascript"></script> <script type="text/javascript"> </script>

微分方程基础

1. 初始值问题

 

    微分方程描述了未知数和它的导数之间的关系。解一个微分方程就是要找到一个关系来满足这个方程，有时候也要同时满足一些附加条件。这里主要讨论常微分方程，比如下面的形式。

 

 

    这里f是已知函数，x是该方程的状态（比如可以表示位移，大小等等），是x的导数。一般这里讨论的x和都是向量。在一般初始值问题中，在一个起始时刻，给定一个，我们希望能知道在一段时间后x的状态。

    一般的微分方程可以很简单的来可视化。在一个2D平面中，这个方程描述了P点在平面上的运动曲线轨迹。在平面上任一点P，函数f可以计算出一个二维向量，所以函数f在平面上定义了一个向量场。如下图

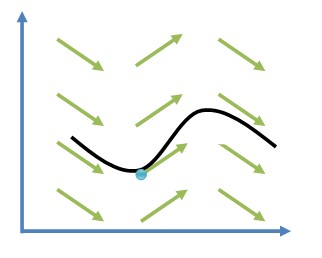
在x的向量是一个速度向量，它把点P从一个位置移动到另一个位置，从向量场的任意一个位置放入一个点P，那么这个向量场就会把P点移动到另一个位置。一但放入了点P，P点的运动状态就由这个函数f来决定。而且P点的运动轨迹还取决于在什么地方放下的P点。

    一个关于x和t的函数，但是它的导数不一定直接依赖于时间。如果依赖于时间，那么P点和向量场都要移动，所以P点在x的速度不仅取决于从什么地方把它放入向量场，而且还取决于P点什么时候到达x点。在这种情况下，有两种方式取决于时间：第一，这个导数自己随时间的变化，第二，点P在不同时刻有不同的导数。

 

 

2.欧拉方法(Euler's Method)

 

    解微分方程最简单的数值方法叫做欧拉方法。给定一个x的初始值，用来近似一段时间h后的值，这里h是时间的步长。欧拉方法简单的在x的导数的方向上近似计算出的值。

    我们也可以用图形来可视化欧拉方法。欧拉方法近似代替了真正的积分曲线，P点的运动轨迹就是下图中的多边形，如下图。

 

虽然欧拉方法很简单，但是不精确。从上图可以看到，时间不长越长，近似的曲线越不精确。而且欧拉方法还不稳定。比如函数，它的积分曲线应该让P点以指数的方式接近于某常数，对于足够小的步长，我们可以精确的近似出曲线，但当时，有，所以这个解相对于常数上下摆动。当h超过2/k，摆动很剧烈，如下图。

 

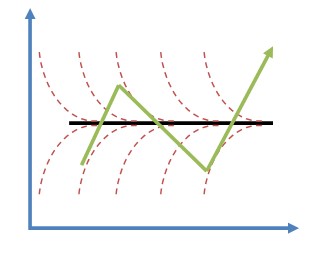
3.中点方法(Midpoint Method)

    欧拉方法有很简单，但是他的缺点也是很明显的，还有一种叫做中点方法的数值微分方程的解法，它比欧拉方法更精确。由泰勒展开式

来计算的。因为

 

 所以有

 

 现在我们取

 

 带入前面的等式，可以得到

 

 移项整理后

 

*原创内容，转载请注明出处*