转载请注明:http://blog.csdn.net/zhangping1987/article/details/25368183
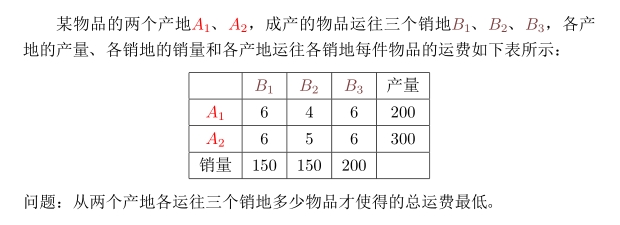
在理解EMD距离模型时,需要先对《运筹学》中运输问题,做一下了解。下面给出几个运输问题的小例子,作为补充知识:
那么,对于上述问题我们发现是一个 产量=销量=500 ,即产销平衡的问题,可以提出这样的数学模型:
假设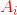
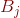
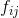
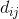
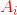
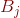
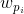
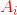

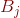
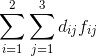
还有令两种可能就是 产量>销量 或者 产量<销量,这里不做模型的讨论,上面三种运输问题都可以用单纯形法进行求解。因为只有当“产量=销量”即: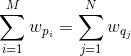
以下给出EMD距离的具体定义和相关证明
————————————————————————————————————————————————————————————————————————————
EMD是由 2000年YOSSI RUBNER在《The Earth Mover's Distance as a Metric for Image Retrival》论文中提出的。
设
其中
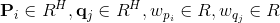
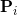
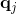
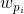
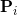
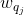
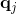
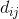
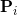
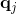
通过以下最优化问题:
解出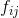
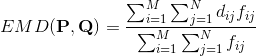
我们知道距离定义必须满足三点:正定性,齐次性,三角不等式,正定性和齐次性很容易证明。下面主要证明三角不等式。作者YOSSI RUBNER证明了,当
时,EMD是满足三角不等式的,即EMD是距离。
所以注意:在使用EMD距离时,要让权重的和是相等的。
三角不等式:
设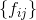
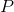
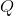
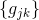
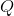
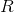
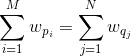
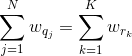
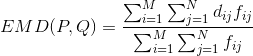
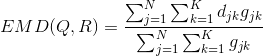
需要证明三角不等式: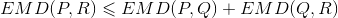
证明:我们首先找到从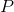
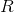
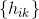
我们设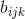
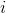
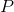
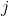
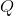
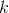
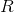
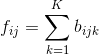
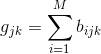
令:
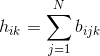
下面证明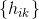
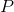
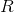
第四个约束条件:
均满足四个条件,所以,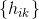
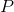
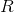
所以,EMD就是在“产销平衡”时是实实在在的距离。
————————————————————————————————————————————————————————————————————————————
在作者的个人主页给出了C代码。
OPencv也已经实现了EMD,我们用EMD距离比较两个直方图,下面说一下,用OPencv中的EMD函数注意事项:
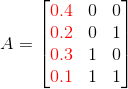
注意:红色一列是每一行特征的权重,权重后边是坐标,我们看到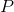
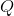
代码我不写了,就把上面这个矩阵放入Mat,然后带入EMD这个函数即可。
在原论文中只证明了总权重相等时,EMD才是距离,但是在Opencv的手册,介绍EMD说,总权重可以不相等,这一点比较困惑!
2014年8月5日,我在做基于颜色的图像检索时,发现EMD距离,也可以做三维直方图
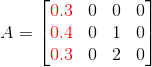
————————————————————————————————————————————————————————————————————————————
第一次,写关于计算机视觉的文章,请大家批评指正!!欢迎回帖!








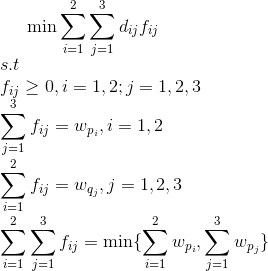
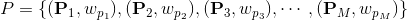
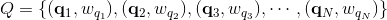
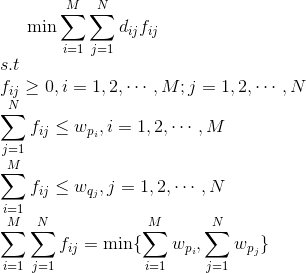
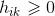
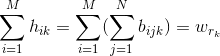
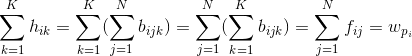
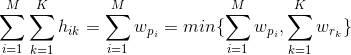
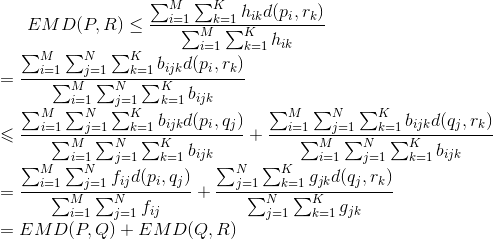
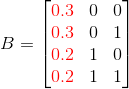















 338
338

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








