ML—EM

Andrew Zhang
May 7, 2016

EM算法是一个求解极大似然估计问题的迭代算法。EM算法对于给定的初始值都能够保证收敛，但不能保证全局收敛，对初始值敏感。

一、EM算法引入
如果现在有一批服从于一个高斯分布的采样样本，想根据样本推测高斯分布的均值，我们知道只需要写出似然函数进行求导即可求解，并且这个高斯分布均值的极大似然估计就是所有采样样本的均值。
现在，让问题稍微复杂点，如果这批样本采样于一个混合高斯分布，这样该怎么算呢？一个有趣的思路就是大胆运用上面所说的简单情况，对每一个高斯核计算所有样本对于这个核的加权均值，这里的权取该样本属于该核的概率，然后根据各个高斯核，更新各个样本属于每个高斯核的概率。迭代。。。直到收敛。这个想法很大胆，但是到底这样做有没有理论依据呢？这就是本文要解决的问题。

二、Jensen不等式
在$n$维线性空间里面，如果有$f''(X) \geq 0$(即$f(X)$是下凸函数)，则有$E[f(X)] \geq f(E[X])$。

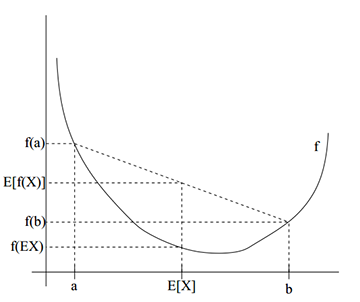
条件更严格一点，要求$f(X)$是严格的下凸函数$(f''(x) > 0)$时，$E[f(X)]=f(E[X])$的充要条件为随机变量$X$是一个单点分布($X$取某个值的概率为1)。
上凸函数结论有此类似的性质。

三、EM算法
假设有m个相互独立的训练样本$\{x^{(1)},x^{(2)},...,x^{(m)}\}$服从于一个分布类型已知，但参数未知的先验分布，常规的思路就是将每个样本取样概率用模型参数表示出来，根据极大似然法求解模型参数，得到估计模型。
$L(\theta)=\prod_{i=1}^{m}{p(x^{(i)};\theta)} \tag{3-1}$
并且往往为了计算方便一般采用公式(3-1)所示的对数形式。
$l(\theta)=\sum_{i=1}^{m}{\log p(x^{(i)};\theta)} \tag{3-2}$
公式(3-2)可以解决大多数的极大似然估计问题，但是有一些问题用公式(3-2)求解会变得特别麻烦，甚至无法求解，明显的例子就是包含隐变量的极大似然估计问题。
$l(\theta)=\sum_{i=1}^{m}{\log p(x^{(i)};\theta)}=\sum_{i=1}^{m}{\log \sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta)}\tag{3-3}$
由于(3-3)里面含有对数函数，并且对数函数里面包含关于参数$\theta$的求和运算，因此对(3-3)求偏导的结果会发现特别复杂麻烦。为了使得上述问题的求解变得简单，EM算法通过迭代增加$l(\theta)$的下确界的似然性，”曲线救国”，$l(\theta)$的下确界求法如下
$l(\theta)=\sum_{i=1}^{m}{\log \sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta)}$
　 　
　 　$=\sum_{i=1}^{m}{\log \sum_{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}}$

　 　$\geq \sum_{i=1}^{m}{\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}}$
$\tag{3-4}$
为了利用Jensen不等式，公式(3-4)对每个$p(x^{(i)},z^{(i)};\theta)$引入了一个辅助概率密度$Q_i(z^{(i)})$，由Jensen不等式知($\sum_{z^{(i)}}Q_i(z^{(i)})=1,Q_i(z^{(i)})\geq 0$)。
定义一个新的变量$J(Q,\theta)$如下,
$J(Q,\theta)=\sum_{i=1}^{m}{\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}} \tag{3-5}$
注：其实$J(Q,\theta)$用$J(\theta)$表述会更准确，因为本文后面会详细说$Q_i(z^{(i)})$怎么由(3-4)这一步确定。
这样公式(3-4)说的就是对于任意的参数$\theta$都有$l(\theta)\geq J(Q,\theta)$，并且发现对于$J(Q,\theta)$虽然包含对数函数，但是每个对数函数里面都不包含求和操作了，这样将大大简化对$\theta$的求导运算。
由于$\log$函数是严格的上凸函数，在这里由严格上凸函数的jensen不等式的性质$f(E[X])\geq E[f[X]]$)，当且仅当$X$是单点分布(常数)时取等号，可得(3-4)取等号时有
$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=C(C表示常数) \tag{3-6}$
也即
$Q_i(z^{(i)}) ∝ p(x^{(i)},z^{(i)};\theta) \tag{3-7}$
又因为$\sum_zQ_i(z^{(i)})=1$可以更进一步的有，

$Q_i(z^{(i)})=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum_zp(x^{(i)},z;\theta)}$

　　　 　$=\frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)}$
　　　 　
　　　 　$=p(z^{(i)}|x^{(i)};\theta)$
$\tag{3-8}$
综上可得，在当前参数$\theta$下，$Q_i(z^{(i)})=p(z^{(i)}|x^{(i)};\theta)$的时候$J(Q,\theta)=l(\theta)$。这里也是可以利用逐步增加$J(Q,\theta)$的似然性来提高$l(\theta)$似然性的关键一步。
接下来，只需要利用前面确定的$Q_i(z^{(i)})$，找到使的$J(Q,\theta)$取极大值的$\hat \theta$即可。然后逐步迭代，直到收敛。

四、EM算法流程
EM算法流程为:
———————————————————————————————–
$Algorithm1:$
Repeat until convergence
　　　(E-step) For each i, set
　　　　　　$Q_i^{(t)}(z^{(i)})=p(z^{(i)}|x^{(i)};\theta^{(t)})$
　　　(M-step) Set
　　　　　　$\theta^{(t)} :=arg\max_{\theta} \sum_{i}\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i^{(t)}(z^{(i)})}$
———————————————————————————————–
EM算法的迭代图示见下图，可见EM算法是通过对隐变量参数和模型参数之间的逐步迭代来逐步提高公式(1-2)的似然性。

注：EM算法主要分两步迭代—E-step：利用现有的模型参数$\theta$，更新每个样本的隐变量分布$Q_i(z^{(i)})$；M-step：利用E-Step得到的每个样本的隐变量分布$Q_i(z^{(i)})$，极大似然估计$J(Q,\theta)$，更新模型参数$\theta$。
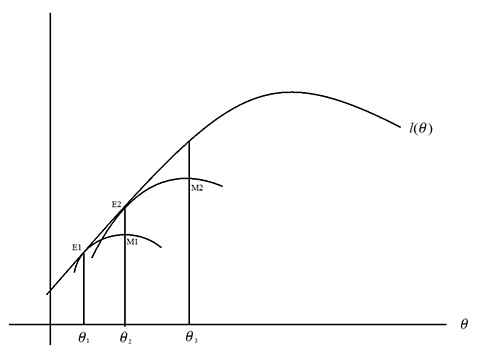
关于EM算法的另一个有助于理解迭代过程的图片如下

五、EM算法的收敛性分析
对于EM算法的迭代过程是否会收敛，由于EM每次迭代提升的是似然函数的下界$J(Q,\theta)$，只需要看看相邻两次迭代过程中$J(Q,\theta)$是否增加即可。
设第t次算法迭代的M-step以后$J(Q,\theta)$为
$J(Q^{(t)},\theta^{(t)})=\sum_{i=1}^{m}{\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}} \tag{5-1}$
对于符号$Q^{(t)}$，假设表示$l(\theta^{(t)}) \geq J(Q^{(t)},\theta^{(t)})$取等号时的$Q^{(t)}$。
因此只需要证明$J(Q^{(t+1)},\theta^{(t+1)})\geq J(Q^{(t)},\theta^{(t)})$即可证明EM算法的局部收敛性。
根据第t+1步迭代的M-step显然有
$J(Q^{(t+1)},\theta^{(t+1)})\geq J(Q^{(t+1)},\theta^{(t)})\tag{5-2}$
其中，
$J(Q^{(t+1)},\theta^{(t)})=\sum_{i=1}^{m}{\sum_{z^{(i)}}Q_i^{(t+1)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t+1)}(z^{(i)})}} \tag{5-3}$
由EM算法的E-step部分得到的公式(3-1)可得
$J(Q^{(t+1)},\theta^{(t)})=l(\theta^{(t)}) \geq J(Q^{(t)},\theta^{(t)}) \tag{5-4}$
综上，已证EM迭代的收敛性。

五、EM算法其它应用
利用EM迭代求解极大似然估计问题的还有很多，例如混合高斯模型，隐马尔科夫模型，混合贝叶斯模型，因子分析等。最近也看到一篇将EM应用于社交网络拓扑结构参数求解的论文。