3、相机参数评估
3.1 原理
相机参数的评估也称为相机定标。要想理解这部分内容,首先应该从成像原理开始讲起。
图6 小孔成像原理
从图6可以看出,真实物体通过小孔映射到成像平面上,小孔到成像平面的距离称为焦距f。在成像平面上的图像是镜像倒立的,所以为了研究方便,在小孔和物体之间定义一个虚拟成像平面(在后面,我们把该平面也称为成像平面),它与小孔的距离也为焦距,则两个成像平面的图像大小是相同的,但虚拟成像平面上的图像与原物体的方向是一样的。
图7 成像的几何模型
我们以小孔为坐标原点建立一个三维直角坐标系XYZ(如图7所示),坐标原点C称为相机的光心。成像平面xy平行于XY,并且距离光心C为f,其中Z轴定义为光轴,它与成像平面xy的交点为P,因此CP=f。设空间中的任一点Q的坐标为(X, Y, Z),该点映射到成像平面的点q的坐标为(x, y,f)。
由几何知识可得:

式中,λ=Z/f,则x=fX/Z,y=fY/Z。因此空间中Q点的三维坐标映射到成像平面的二维坐标q点在齐次坐标下的线性映射关系为:

如图7所示,在成像平面(坐标系为xy)的坐标原点为P,但图像(设坐标系为uv)的坐标原点一般在左上角,所以这两个坐标系之间需要通过平移来进行转换。另外成像平面xy是长度单位,而相机图像传感器的单位是像素,因此像素与长度之间也是需要转换的,而且水平和垂直的像素往往是不相同的,所以横纵轴的转换系数是不一致。因此式32改写为:
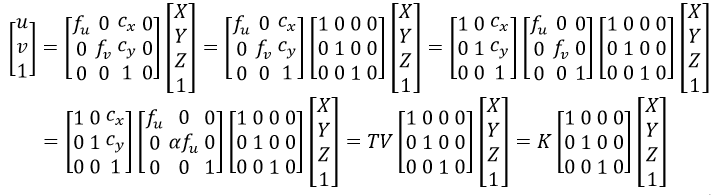
式中,fu和fv为焦距f在横纵轴的长度和像素的转换,它们之间的关系可以写为fv=αfu,(cx, cy)为坐标平移。因为矩阵K的参数都是基于相机内部自身的参数,因此K称为相机内参数,K=TV。
相机除了具有内参数外,还有外参数。式33中的(X, Y, Z)称为相机坐标,而它与真实的世界坐标(X’, Y’, Z’)还存在欧几里得变换,即:
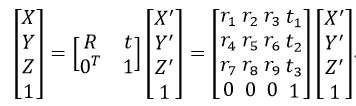
式中,R为3×3的旋转矩阵,t为3×1的平移向量。式34代入式33,得

式中,[R|t]称为相机外参数,M称为投影矩阵。
如果得到的两幅图像如图3所示的那样,即相机在三角架上通过旋转得到的两幅图像,则对于同一个世界坐标上的点(X’, Y’, Z’),在两幅图像上的坐标点分别为(u0, v0)和(u1, v1),即:
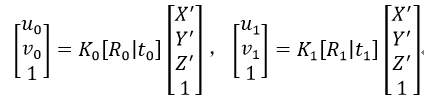
由于相机只做旋转处理(或者我们认为物体离相机很远),则t0=t1=0,从而得到(u0, v0)和(u1, v1)的关系为:

式中,R10为由图像1到图像0的相对旋转矩阵,R10=R1R0-1。由式2可得:
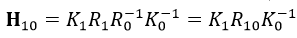
为简单起见,我们设两幅图像的相机内参数中的坐标平移都为0,即K=V,因为抛弃参数T对图像拼接影响不大。
我们在评估焦距时,还需定义f1u=f1v=f1,f0u=f0v=f0,即设图像的长宽等像素:

则式38表示为
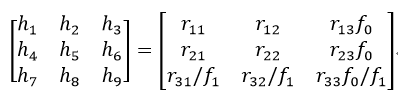
式中,R10=[rij]。
由式40我们就可以得到焦距f0和f1:观察矩阵R10可知,R10前两行一定有相同的范数,并且是正交的,因此

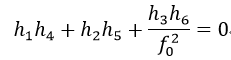
由式41可得:
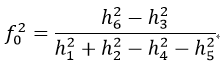
由式42可得:
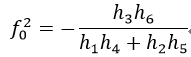
由式43和式44得到了两个f0,选取哪个呢?比较式43和式44中分母部分的绝对值的大小,如果式43的分母大,则选择分式大的值作为f0,否则如果式44的分母大,则选择值小的作为f0。
同理,矩阵R10的前两列也一定有相同的范数,并且也是正交的,因此
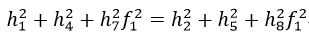

由式45可得

由式46可得
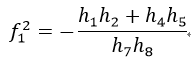
比较式47和式48中分母部分的绝对值的大小,如果式48的分母大,则选择分式大的值作为f1,否则如果式47的分母大,则选择值小的作为f1。
如果两幅图像的焦距相同,则最终这两幅图像的焦距f为:
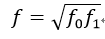
当评估计算得到多个f时,可取这些f的中值作为所有相机的焦距。
焦距得到后,我们就可以由式38得到R10:
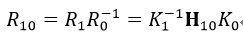
则R01(由图像0到图像1的相对旋转矩阵)为:

则
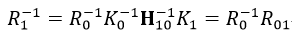
对于刚性物体,它的旋转都是沿笛卡尔坐标系的x轴、y轴和z轴旋转,则分别沿着这三个轴的旋转矩阵定义为:

则旋转矩阵R表示为:
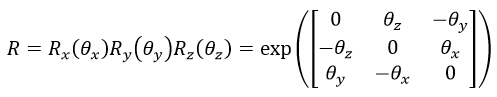
三维旋转除了可以用旋转矩阵描述外,还可以用旋转向量r描述,即r=[rx, ry, rz]T。旋转向量的长度(模)表示绕轴逆时针旋转的角度θ。旋转向量和旋转矩阵可以通过Rodrigues算法进行转换。由旋转向量转换为旋转矩阵的Rodrigues算法描述如下:
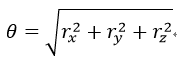

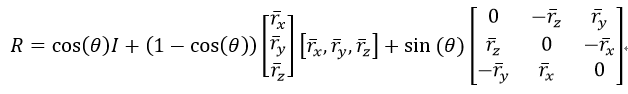
式中,I为3×3的单位矩阵。而由旋转矩阵转换为旋转向量的Rodrigues算法公式为:
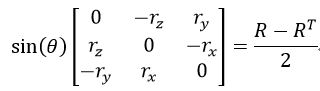
当有多幅图像需要拼接为一幅图像时,是要以其中一幅图像为基准,其他图像都要旋转到该基准图像平面上的,所以就需要找到基准平面。这里用到的算法为最大生成树算法。
待拼接图像的排列是无序的,而且我们事先是不知道它们之间的关系的,我们只知道它们之间的单应矩阵,而单应矩阵是由图像间的内点计算评估得到的。由此我们可以构造一个无向图G,G的节点为图像,G的边为内点数,然后利用并查集在该G中得到一棵最大生成树。
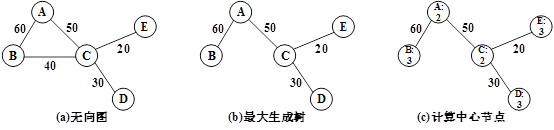
图8 最大生成树
图8为用于拼接的最大生成树的一个例子,图(a)为无向图,节点为图像(A、B、C、D、E),节点间的边为内点数。图(b)为最大生成树,由图像C到图像B要经过最大的边连接,所以要经过图像A,而图像C和图像B之间的连接就需要去掉了。
我们把树的中心节点作为基准图像。中心节点的确定方法为:计算每一个节点到所有叶节点的距离,把其中的最大值作为该节点的值;然后选择这些值中最小者作为中心节点。这里的距离指的是节点间的节点数。如图8(c)所示,节点A和C为中心节点。中心节点可能是1个,也可能是2个,如果是2个,则选择其中一个即可。
基于以上方法,我们得到了相机的内外参数,但这样得到的参数忽略了多个图像间的约束,而且会产生累计误差。这时,我们就需要用到光束平差法(Bundle Adjustment)来精确化相机参数。光束指的是相机光心“发射”出来的光束(或射线),它透过相片达到物点,因此相片中的点应该和物点处于一个光束线上,但当两者不共线时,我们就需要对结构和视角参数进行调节,以达到最优解甚至共线的目的。最优化一般采用前文介绍过的LM算法。
应用于光束平差法的LM算法,误差指标函数可以有两个,一个是重映射误差,另一个是射线发散误差。
重映射误差公式为式25(即一个内点要有x轴和y轴两个误差值),而单应矩阵H是由式38得到。也就是说H是由相机的内外参数得到。相机的内外参数一共有7个:fu、α、cx、cy、rx、ry和rz。前4个参数是内参数(见式33),后3个参数是外参数(即式55中的旋转向量的三个元素)。因此式25中的h为h(fu, α, cx, cy, rx, ry,rz),由此得到J(h)为:
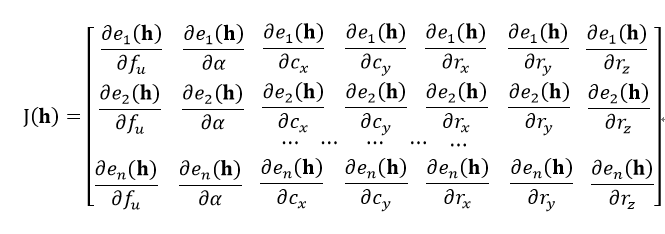
式中,n表示待拼接的图像数量,也就是所有的相机。有时为了计算方便,导数可以用差分近似,例如我们要计算e对fu的偏导,则
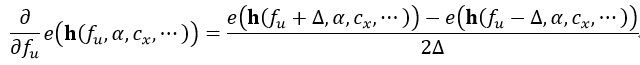
式中,∆表示一个很小的数。
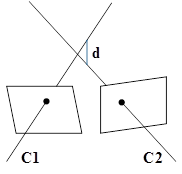
图9 射线发散概念
第二种误差指标函数是基于射线发散原理。如图9所示,不同的相机发出的射线透过相片后达到同一个物点,但由于误差,两条射线不会相交,或者称为两条射线发散了,我们就把这两条射线间的最短距离d定义为射线发散误差。
下面,我们不加证明的给出射线发散误差的计算公式:
设(u1, v1, 1)和(u2, v2, 1)为两幅不同图像的同一特征点的齐次坐标,则由单应矩阵H1和H2分别得到它们的物点坐标为:

分别对坐标进行归一化处理:
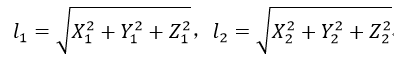
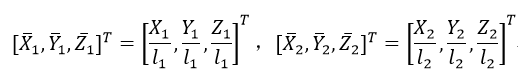
为了简化计算,射线间的最短距离可以表示为基于不同焦距f1和f2下的归一化后的物点坐标之差:

式64说明在计算射线发散误差时,每一个内点有x轴、y轴和z轴三个误差值。
我们假设射线就是相机的光轴,因此单应矩阵H中的参数α=1,cx=cy=0,所以式25中h只是基于4个参数的变量,即h(fu, rx,ry, rz),由此得到射线发散误差的J(h)为:

前面介绍的光束平差法会引起波形效应,即拼接的图像会呈现蛇形分布,这是因为真实拍摄相片时不大可能都保持水平而不倾斜的,也就是重力轴没有垂直于图像。因此我们就需要引入一个全局校正矩阵Q,用于“拉直”拼接图像,该方法也成为波形校正。
校正的目的应该是,在第k个相机旋转矩阵Rk乘以Q后,全局y轴应该与图像的x轴垂直,这种约束条件可以表示为:
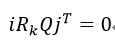
式中,i=(1, 0, 0),j=(0, 1, 0),该式的含义是Rk的第一行rk0垂直于Q的第二列q1。式66的这类约束问题可以看成是最小二乘问题:

因此,q1是矩量矩阵∑rTr的最小特征值所对应的特征向量。矩阵Q的其他列的经验公式为:

式中,×表示矩阵的点乘(即对应元素相乘,与MATLAB中的点乘相同),分母表示对分子取模,即q0是归一化的结果。
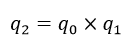
最终的全局校正矩阵Q=[q0 q1 q2],而用Q乘以各个相机的R即实现了波形校正。如果要进行垂直校正拉直,则需选择最大特征值对应的特征向量。
3.2 源码
Estimator类是相机参数评估器的基类,HomographyBasedEstimator和BundleAdjusterBase都是Estimator类的子类。HomographyBasedEstimator类主要负责相机参数的计算评估,BundleAdjusterBase类主要通过光束平差法使相机参数精确化。
我们先来看HomographyBasedEstimator类,它的主要内容就是estimate函数:
void HomographyBasedEstimator::estimate(const vector<ImageFeatures> &features, const vector<MatchesInfo> &pairwise_matches,
vector<CameraParams> &cameras)








 本文深入探讨了OpenCV2.4.9中的相机参数评估,包括相机定标原理、几何模型、内外参数计算、相对旋转矩阵的获取。通过对图像拼接过程中的相机参数优化,利用光束平差法和最大生成树算法,实现精准的图像拼接。同时,文章详细介绍了波形校正方法,以消除拼接图像的波形效应。
本文深入探讨了OpenCV2.4.9中的相机参数评估,包括相机定标原理、几何模型、内外参数计算、相对旋转矩阵的获取。通过对图像拼接过程中的相机参数优化,利用光束平差法和最大生成树算法,实现精准的图像拼接。同时,文章详细介绍了波形校正方法,以消除拼接图像的波形效应。


 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








