二元一次不定方程

一、假设(x0,y0)为a*x + b*y = c  (a,b,c,x,y为整数，a、b互质)的一组解，证明该不等式的通解为：(x0 + k*b,y0 - k*a);

证明：

1、首先将(x0 + k*b,y0 - k*a)带入原方程，使得方程成立，说明这些解为原方程的解。

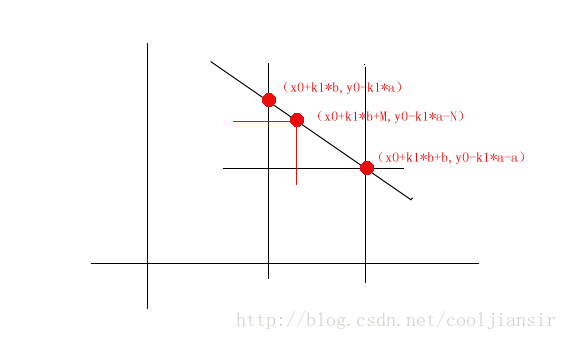
2、假设除了这些解之外还存在至少一个解(x1,y1),这个点坐落在（x0+k1*b,y0-k1*a）和（x0+（k1+1）*b,y0-（k1+1）*a）之间，如下图所示：

如果（x1，y1）是这两点连成线段的的n等分点（2等分、3等分......n等分点），那么a和b具有公约数n。

如果（x1,y1）不是这两点连成线段的n等分点，那么可以还可以等间隔找出其他的解：

其中最后一个点与（x0+(k1+1)*b,y0-(k1+1)*a）的横坐标距离为（|b|%|M|）,

然后又可以以（|b|%|M|）等间距找到一系列点，就像辗转相除法一样最终可以找到为b的约数的距离（可以为1），一旦找到这样的点（n1等分点）同样说明a和b具有公约数n1.与题设a，b互为质数矛盾。

二：

对于方程 a*x + b*y = 1  (a,b,x,y为整数，a、b互质)---------------------------------(1式)

设a/b = k,a%b = t;则a = b*k+t；

原方程变形为：

(b*k+t)*x + b*y = 1;

即b*(k*x+y) + t*x = 1;-----------------------------------------------------------------------(2式)

2式与1式为同样的问题，只是参数有a,b变成了b，t（参数减小了，相当于问题规模缩小了），因此可以设计一个递归的方法解这个方程。

/*

 * test.cpp
 *
 *  Created on: 2013-8-28
 *      Author: zhijian
 */
#include <stdio.h>


int gcd(int a,int b){
return a?gcd(b%a,a):b;
}
int extends_gcd(int a,int b,int &x,int &y){
if(b==0){
x = 1;
y = 0;//这里可以为任意整数值
return a;
}
int tempx;
int result = extends_gcd(b,a%b,tempx,y);
x = y;
y = tempx - a/b*x;
return result;
}
void F(int a,int b,int c){
int x0,y0;
int gc = gcd(a,b);
a /= gc;
b /= gc;
c /= gc;
extends_gcd(a,b,x0,y0);
printf("%d*x+%d*y=%d的通解为：(%d+k*%d,%d-k*%d)\n",a,b,c,x0*c,b,y0*c,a);
}




int main(){
F(111,-321,75);
return 0;
}