R假设检验之Breusch-Pagan检验(Breusch-Pagan Test)
目录
R假设检验之Breusch-Pagan检验(Breusch-Pagan Test)

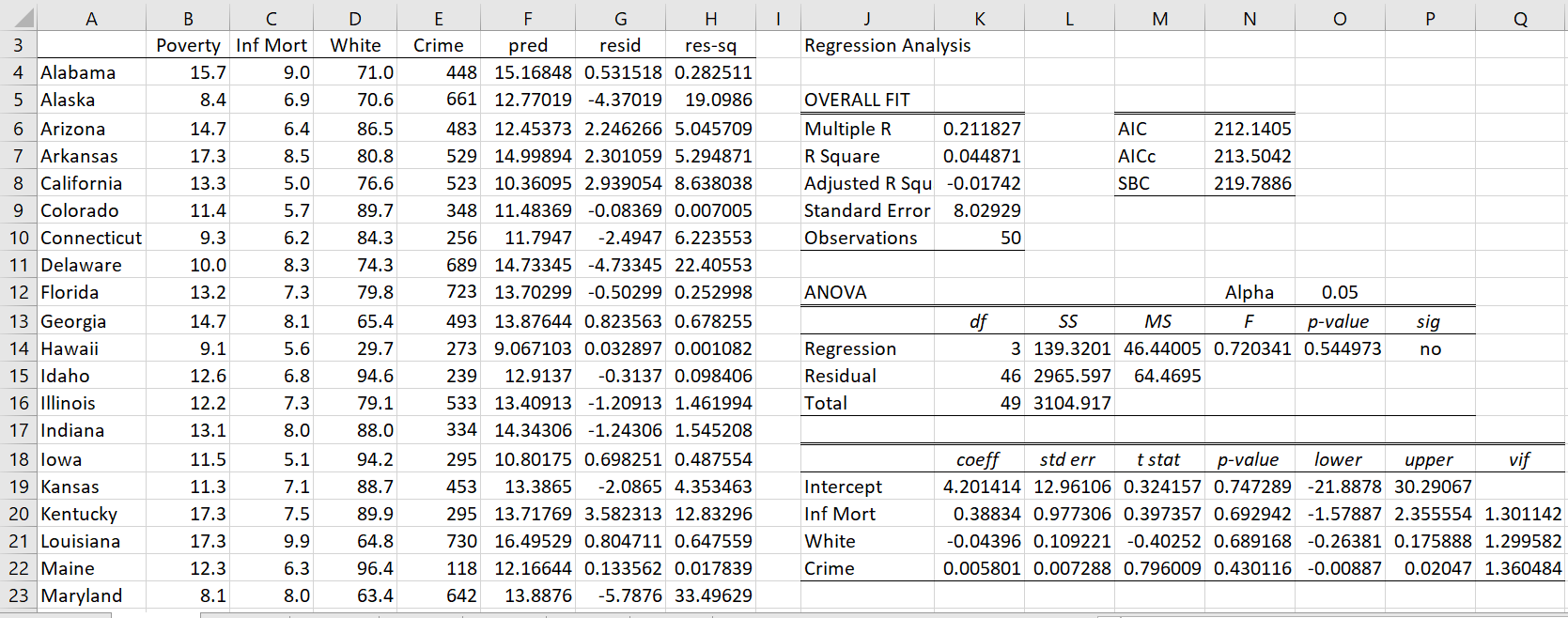
Breusch-Pagan检验用于确定在回归分析中是否存在异方差(heteroscedasticity)。
我们将使用内置的数据集mtcars拟合一个回归模型,然后使用lmtest库中的bptest函数执行一个Breusch-Pagan检验,以确定是否存在异方差。
目录
R假设检验之Breusch-Pagan检验(Breusch-Pagan Test)


Breusch-Pagan检验用于确定在回归分析中是否存在异方差(heteroscedasticity)。
我们将使用内置的数据集mtcars拟合一个回归模型,然后使用lmtest库中的bptest函数执行一个Breusch-Pagan检验,以确定是否存在异方差。
 1874
1874
 10万+
10万+
 1297
1297
 943
943
 854
854
 762
762

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?



打赏作者