跟着吴恩达学深度学习（一）

Zhoozie

已于 2024-07-25 21:15:03 修改

阅读量481

点赞数 11

分类专栏：深度学习文章标签：深度学习 python 笔记人工智能

于 2024-07-02 17:44:50 首次发布

本文链接：https://blog.csdn.net/zhoozie/article/details/140131860

版权

深度学习专栏收录该内容

6 篇文章 0 订阅

订阅专栏

前言

本文对应了吴恩达深度学习系列课程中的第一门课程《神经网络和深度学习》。本门课程将会详尽地介绍深度学习的基本原理。

第一门课程授课大纲：

深度学习概论
神经网络基础
浅层神经网络
深层神经网络

1 深度学习概论

略...

2 神经网络基础

2.1 二元分类

logistic回归是一个用于二分类（Binary Classification）的算法。二分类就是输出结果 y 只有 0 和 1 两个标签。

以一个图像识别为例，例如识别猫，1代表猫，0代表不是猫。用y表示输出的结果标签。

Notation：

用一对(x,y)表示一个单独的样本，其中x是n_x维的特征向量， $y\epsilon \left \{ 0,1 \right \}$ 。训练集大小为m。train为训练集，test为测试集。

训练集： $\left ( x^{(1)},y^{(1)} \right ),\left ( x^{(2)},y^{(2)} \right )...\left ( x^{(m)},y^{(m)} \right )$

2.2 logistic回归

在逻辑回归中， $\hat{h}=P(y=1|x)$ 表示y为1的概率，取值范围是(0,1)之间。

已知的特征输入向量 x 可能是 $n_x$ 维度，logistic回归的参数 w 也是 $n_x$ 维的向量，而 b 就是一个实数。所以已知输入x和参数w和b，我们如何计算输出预测 $\hat{y}$ ？ $\hat{y}$ 是预测的概率，应该介于0-1之间。逻辑回归的线性预测输出可以写成如下格式：

$\hat{y}=\sigma(w^Tx+b)$

Sigmiod函数是一种非线性的S型函数，输出范围是[0,1]，通常在神经网络中当激活函数（Activation function）。表达式如下：

$\sigma(z)=\frac{1}{1+e^{-z}}$

2.3 logistic 回归损失函数

逻辑回归中，w和b都是未知参数，需要反复训练优化得的。为了训练logistic回归模型的参数w以及b，需要定义一个成本函数（cost function）。为了让模型通过学习调整参数，要给一个m个样本的训练集，很自然地，你想通过在训练集找到参数w和b，来得到输出。

对于m个训练样本，通常使用上标来表示对应的样本。例如（表示第i个样本）： $(x^{(i)},y^{(i)})$

如何定义所有m个样本的cost function呢？先从单个样本出发，希望该样本的预测值与实际值越相似越好。

Loss(error) function：损失函数（误差函数），可以用来衡量算法的运行情况。函数定义如下：

$L(\hat{y},y)=-y\log{\hat{y}}+(1-y)\log{(1-\hat{y})}$

在logistic回归中，对于这个损失函数，需要让它尽可能的小。

例子：

(1)y=1时， $L=\log(\hat{y})$ 想要足够小， $\hat{y}$ 就要足够大，最大最大不能超过1。

(2)y=0时， $L=-\log(1-\hat{y})$ $-\log(\hat{y})$ 想要足够小， $1-\hat{y}$ 要足够大， $\hat{y}$ 就要足够小，最小不能小于0。

损失函数是在单个训练样本中定义的，它衡量了在单个训练样本上的表现。

下面定义一个成本函数，它衡量的是在全体训练样本上的表现。成本函数J是根据之前得到的两个参数w和b，J(w,b)=损失函数求和/m.，即所有m个训练样本的损失函数和的平均。

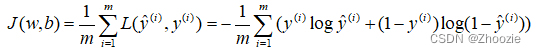
成本函数(cost function)是关于未知参数w和b的函数，我们的目标是在训练模型时，要找到合适的w和b，让成本函数J尽可能的小。

结果表明，logistic回归可以看成是一个非常小的神经网络。

2.4 梯度下降法

凸函数（convex function）的局部优化特性是logistic回归使用这个成本函数J的重要原因之一。使用梯度下降法很快地收敛到局部最优解或者全局最优解。

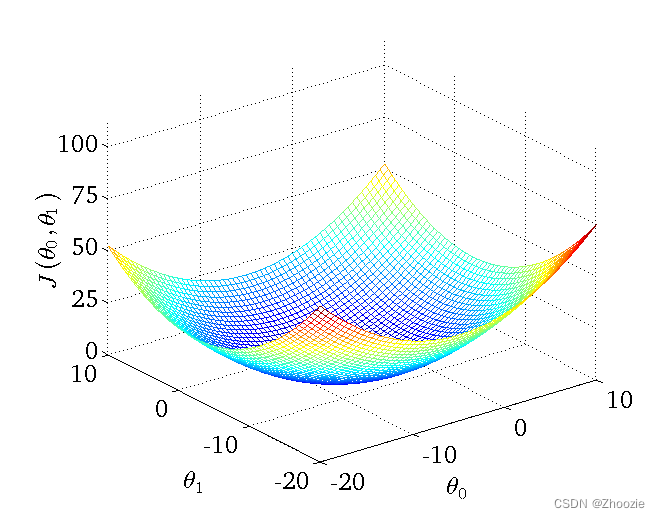
由于J(w,b)是凸函数，梯度下降算法（Gradient Descent）步骤如下：

（1）初始化，随机选组一组参数w和b值，

（2）每次迭代的过程中分别沿着w和b的梯度（偏导数）的反方向前进一小步，不断修正w和b。

（3）每次迭代更新w和b后，都能让J(w,b)更接近全局最小值。

梯度下降算法每次迭代更新，w和b的修正表达式为：

$w:= w-\alpha\frac{\partial J(w,b)}{\partial w}$

$b:=b-\alpha\frac{\partial J(w,b)}{\partial b}$

其中， $\alpha$ 是学习因子（learning rate），表示梯度下降的步进长度，其值越大，w和b每次更新的“步伐”更大一些；越小，更新“步伐”更小一些。

2.5 导数

略...

2.6 更多导数的例子

略...

2.7 计算图

略...

2.8 计算图的导数计算

略...

2.9 logistic 回归中的梯度下降法

对单个样本而言，逻辑回归损失函数(Loss function)表达式如下：

$z=w^Tx+b$

$\hat{y}=a=\sigma(z)$

$L(a,y)=-(y\log(a)+(1-y)\log(1-a))$

逻辑回归的正向传播过程（已知w和b，求损失函数）：

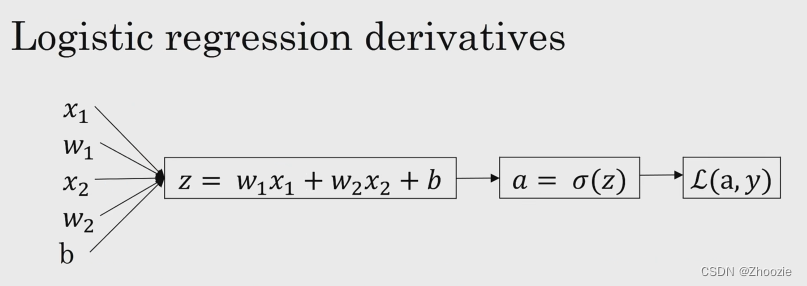
逻辑回归的反向传播过程（已知损失函数，计算参数w和b的偏导数）：

2.10 m 个样本的梯度下降

m个样本梯度下降算法流程如下所示：

#1.初始化
J=0; dw1=0; dw2=0; db=0;
#2.for循环遍历训练集，并且计算相应的每个训练样本的导数
for i = 1 to m
    z(i) = wx(i)+b;
    a(i) = sigmoid(z(i));
    J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i));
    dz(i) = a(i)-y(i);
    dw1 += x1(i)dz(i);
    dw2 += x2(i)dz(i);#n=2,两个特征w1,w2
    db += dz(i);
#3.最终对所有的m个训练样本都进行了这个计算，你还需要除以m，计算平均值
J /= m;
dw1 /= m;
dw2 /= m;
db /= m;

2.11 向量化

如上小节的代码所示，假使特征的数量不止是 2 个，而是有 n 个就需要一个循环来进行计算，此时就有了两层循环，会降低代码的执行效率。在深度学习领域会常常训练一个越来越大的数据集，代码的高效就显得尤为重要。据此，引出了本小节学习到的向量化技术，它可以使你摆脱上小节代码中的显式循环，使你的代码更为高效。

import numpy as np
 
a = np.array([1,2,3,4])
print(a)
 
#[1 2 3 4]

import time 
a = np.random.rand(1000000)
b = np.random.rand(1000000)
 
tic = time.time()
c = np.dot(a,b)
toc = time.time()
 
print(c)    #249866.84361136454
print("向量化版本:" + str(1000*(toc-tic)) + "ms")    #向量化版本:1.9810199737548828ms
 
c = 0
tic = time.time()
for i in range(1000000):
    c += a[i]*b[i]
toc = time.time()
 
print(c)    #249866.8436113724
print("非向量化版本:" + str(1000*(toc-tic)) + "ms")    #非向量化版本:531.0003757476807ms

从上述运行结果看出，向量化之后运行速度会大幅上升，该例子使用for循环运行时间是使用向量计算运行时间的200多倍。

2.12 向量化的更多例子

示例1：已知矩阵 A 和向量 v，求 u=Av ？

import numpy as np
u = np.dot(A,v)

示例2：已知向量 v ，对向量中的每一个元素进行指数运算？

import numpy as np
u = np.exp(v)

对于2.10 m个样本梯度下降中的代码可以向量化为以下形式：

J = 0,dw = np.zeros(n_x,1)
#上面代码的dw1 += x1(i)dz(i);dw2 += x2(i)dz(i);改为：
dw += X(i)dz(i)
#上面代码的dw1 /= m;dw2 /= m;改为：
dw /=m

将其中的 dw1，dw2 设为向量 dw。

2.13 向量化 logistic 回归

对于 logistic 回归的正向传播步骤，如果有m个训练样本，那么对第一个样本预测需要采用下方公式进行计算：

$z^{(1)}=w^Tx^{(1)}+b$

$a^{(1)}=\sigma(z^{(1)})$

以此类推，需要做m次。结果表明要进行正向传播，需要对m个训练样本都计算预测结果。有一个方法不使用for循环也能做到，具体步骤如下：

（1）定义一个矩阵X来作为你的训练输入，这是一个 $n_x * m$ 的矩阵。

（2）构建一个1*m的矩阵Z来作为你的训练输出，w^T是一个 $1*n_x$ 的矩阵，转置之后的维度是(1,n_x)。b是一个常数值，维度为(1,m)。

$[z^{(1)}z^{(2)}...z^{(m)}]=w^{T}X+[bb...b]=[w^{T}x^{(1)}+b w^{T}x^{(2)}+b...w^{T}x^{(m)}+b]$

（3）构建sigmiod函数，求a

具体代码如下：

import numpy as np
Z = np.dot(w.T,X) + b  #w.T表示w的转置，b为1*1，Z为1*m矩阵
#python中自动将b拓展为一个1*m的行向量，这个操作在python中叫做广播(broadcasting)
A = sigmoid(Z)

2.14 向量化 logistic 回归的梯度输出

对于整个logistic回归向量化，for循环尽可能用矩阵运算代替，对于单次迭代，梯度下降算法流程如下所示：

Z = np.dot(w.T,X) + b
A = sigmoid(Z)
dZ = A-Y
dw = 1/m*np.dot(X,dZ.T)
db = 1/m*np.sum(dZ)
 
w = w - alpha*dw
b = b - alpha*db

其中，alpha是学习因子，决定w和b的更新速度。上述代码只是对单次训练更新而言的，外层还需要一个for循环，表示迭代次数。

2.15 Python 中的广播

下图是不同食物（每100g）中不同营养成分的卡路里含量表格，表格为3行4列，列表示不同的食物种类，从左至右依次为苹果，牛肉，鸡蛋，土豆。行表示不同的营养成分，从上到下依次为碳水化合物，蛋白质，脂肪。那么，如果现在想要计算不同食物中不同营养成分中的卡路里百分比。

现在计算苹果中的碳水化合物卡路里百分比含量，首先计算苹果（100g）中三种营养成分卡路里总和 56+1.2+1.8=59，然后用56/59=94.9%算出结果。对于其他食物，计算方法类似。

import numpy as np
A = np.array([[56.0,0.0,4.4,68.0],
             [1.2,104.0,52.0,8.0],
             [1.8,135.0,99.0,0.9]])
 
print(A)
 
#[[ 56.    0.    4.4  68. ]
# [  1.2 104.   52.    8. ]
# [  1.8 135.   99.    0.9]]
 
cal = A.sum(axis=0) #axis=0意味着竖直轴相加，而水平轴是1
print(cal)
 
#[ 59.  239.  155.4  76.9]
 
percentage = 100*A/cal.reshape(1,4) #其实也可以不调用reshape(),但是使用会更保险，时间复杂度为o(1)，调用成本极低
print(percentage)
#[[94.91525424  0.          2.83140283 88.42652796]
# [ 2.03389831 43.51464435 33.46203346 10.40312094]
# [ 3.05084746 56.48535565 63.70656371  1.17035111]]

其他广播的例子：

3 浅层神经网络

3.1 神经网络概览

神经网络的结构与逻辑回归类似，只是神经网络的层数比逻辑回归多一层，多出来的中间那层称为隐藏层或中间层。从计算上来看，神经网络的正向传播和反向传播比logistic回归多了一次重复的计算。

3.2 神经网络表示

上图为一张神经网络结构图，各部分说明如下：

输入特征x1,x2,x3竖向堆叠起来，这是神经网络的输入层（input layer），包含了神经网络的输入
中间一层的四个圆圈，称之为神经网络的隐藏层（hidden layer）。在训练集中隐藏层节点的真实数值我们是不知道的，看不到它们的数值。
最后一个圆圈是输出层（output layer），只有一个节点，它负责输出预测值 $\hat{y}$ 。

在一个神经网络中，当你使用监督学习训练它时，训练集包含了输入x，还有目标输出y。

现在我们再引入几个符号，之前使用向量x表示输入特征，另一种表达方式 $a^{[0]}$ ，而a也表示激活（activations）的意思，它意味着网络中不同层的值会传递给后面的。把隐藏层输出记为 $a^{[1]}$ ，上标从0开始。用下标表示第几个神经元，注意下标从1开始。例如 $a^{[1]}_1$ 表示隐藏层第1个神经元（节点）。

在计算神经网络层数时，不将输入层计算在内，如上层神经网络层数为2（1个隐藏层，1个输出层）。其中 $a^{[0]}$ 中上标的 0 ，即表示输入层。

3.3 计算神经网络的输出

下面的圆圈代表了回归计算的两个步骤，神经网络重复计算这些步骤很多次：

对于两层神经网络，从输入层到隐藏层对应一次逻辑回归运算；从隐藏层到输出层对应一次逻辑回归运算。每层计算时，要注意对应的上标和下标，一般我们记上标方括号表示layer，下标表示第几个神经元。例如 $a^{[l]}_i$ 表示第l层的第i个神经元。

下面，我们将从输入层到输出层的计算公式列出来：（共4个隐藏单元）

然后将等式向量化，提高效率：

向量化时注意：当我们这一层有不同的节点，那就纵向地堆叠起来。

当你有一个单隐层神经网络，你需要用代码实现的是右边四个等式。

3.4 多样本向量化

3.3中介绍了已知单个训练样本时，计算神经网络的预测，在3.4中，将看到如何将不同训练样本向量化。

在书写标记上用上标(i)表示第i个训练实例，例如 $z^{(i)}$ ， $a^{[2](i)}$ 。

接下来将上面的for循环写成矩阵运算的形式：

矩阵的行表示神经元个数，列表示样本数目m。

3.5 向量化实现的解释

上图解释了方程向量化在多样本时的正确实现

⚠️注意：输入矩阵X也可以写成 $A^{[0]}$

3.6 激活函数

本小节将介绍几种常见的激活函数：

（1）sigmoid函数

公式： $a=\frac{1}{1+e^{-z}}$

值域：(0,1)

图像

（2）tanh函数（双曲正切函数）

公式： $a=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$

值域：(-1,1)

图像

tanh函数的平均值更接近0，类似数据中心化的效果，使数据平均值接近0，这实际让下一层的学习更方便一点。使用sigma函数的例外是二分类，在这个例子中，可以隐藏层用tanh函数，输出层用sigma函数。

sigma函数和tanh函数都有一个缺点，如果z非常大或非常小时，那么导数的梯度（函数的斜率）可能就很小，接近0，这样会拖慢梯度下降算法。

（3）ReLU函数（修正线性单元）

公式： $a=\max(0,z)$

值域： $(0,+\infty)$

图像

只要z为正，导数就是1；当z为负时，斜率为0。ReLU的缺点是当z为负时，导数为0，但还有一个版本，带泄露的ReLU。

（4）Leaky ReLU函数（泄漏的ReLU）

公式： $a=\max(0.01z,z)$

值域： $(-\infty,+\infty)$

图像

📜总结：

（1）sigmoid函数除非用在二元分类的输出层，不然绝对不要用，或者几乎从来不用。

（2）tanh函数几乎在所有场合都更优越。

（3）最常用的默认激活函数是ReLU，如果不确定用哪个，就用这个或者也可以试试带泄漏的ReLU。

3.7 为什么需要非线性激活函数？

回顾四个神经网络方程

$z^{[1]}=W^{[1]}x+b^{[1]}$

$a^{[1]}=g^{[1]}(z^{[1]})$

$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$

$a^{[2]}=g^{[2]}(z^{[2]})$

🙋为什么不能使用线性激活函数？

线性激活函数是指形如 $g(z)=z$ 的函数，只将任何输入直接输出。

如果使用线性激活函数或者没有激活函数，那么无论激活函数有多少层，一直在做的只是计算线性激活函数，所以不如去掉全部隐藏层。使用神经网络与直接使用线性模型的效果并没有什么两样。因此，隐藏层的激活函数必须要是非线性的。

如果所有的隐藏层全部使用线性激活函数，只有输出层使用非线性激活函数，那么整个神经网络的结构就类似于一个简单的逻辑回归模型。只有一个地方可以用线性激活函数 $g(z)=z$ ，如果你要机器学习的是回归问题，所以y是实数，比如预测房价，y是实值，那么输出层用线性激活函数也许可行，但是隐藏层不能用线性激活函数。

3.8 激活函数的导数

在梯度下降反向计算过程中少不了计算激活函数的导数即梯度。

针对3.6小节的激活函数，分别求出其导数（具体求导过程省略）。

（1）sigmoid函数

公式： $g(z)=\frac{1}{1+e^{-z}}$

导数： $g^{'}(z)=\frac{d}{dz}g(z)=g(z)(1-g(z))=a(1-a)$

（2）tanh函数

公式： $g(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$

导数： $g^{'}(z)=\frac{d}{dz}g(z)=1-(g(z))^2=1-a^2$

（3）ReLU函数

公式： $g(z)=\max(0,z)$

导数： $g^{'}(z)=\begin{cases} 0\quad z<0\\ 1\quad z\ge0\\\end{cases}$

（4）Leaky ReLU函数

公式： $a=\max(0.01z,z)$

导数： $g^{'}(z)=\begin{cases} 0.01\quad z<0\\ 1\quad\quad z\ge0\\\end{cases}$

3.9 神经网络的梯度下降法

在本小节中，将看到梯度下降法的具体实现，如何处理单隐层神经网络。将介绍为什么特定的几个方程是精准的方程，或者可以针对神经网络实现梯度下降的正确方程。

随机初始化参数很重要，而不是全部初始化为0。总结一下正向传播过程。

3.10 （选修）直观理解反向传播

神经网络相较于逻辑回归，多了一个隐藏层。下图为一个两层神经网络的计算步骤。

总结一下，浅层神经网络（包含一个隐藏层），m个训练样本的正向传播过程和反向传播过程分别包含了6个表达式，其向量化矩阵形式如下图所示：

3.11 随机初始化

在训练神经网络时，随机初始化权重很重要，对于logistic回归，可以将权重参数初始化为零，但如果神经网络的各参数数组全部初始化为0，再使用梯度下降算法，那会完全无效。

如果有两个输入特征，设置W和b为零，导致两个神经元得到相同的结果，因为两个隐藏单元都在做完全一样的计算；当你计算反向传播时，由于对称性结果也是相同的。技术上假设输出的权重也是一样的，意味着节点计算完全一样的函数，完全对称。可以通过归纳法证明。在这种情况下，多个隐藏单元没有意义。对于多个输入特征也是一样的。

解决方法也很简单，就是将W进行随机初始化（b可初始化为零）。python里可以使用如下语句进行W和b的初始化：

W_1 = np.random.randn((2,2))*0.01 #随机初始化 
b_1 = np.zero((2,1)) 
W_2 = np.random.randn((1,2))*0.01 
b_2 = 0

🙋0.01怎么来的？

实际上我们通常把权重矩阵初始化成非常小非常小的随机值，因为如果使用tanh函数或sigmoid激活函数，权重太大是计算出来的值可能落在平缓部分，梯度的斜率非常小，意味着梯度下降法会非常慢，学习过程也会非常慢。

4 深层神经网络

4.1 深层神经网络

深层神经网络其实就是包含更多的隐藏层神经网络。上一章浅层神经网络主要介绍了单隐藏层的神经网络（双层神经网络），本章将学习含隐藏层层数更多的神经网络。严格上来说逻辑回归也是一个一层的神经网络。

⚠️注意：当计算神经网络的层数时，不算输入层，只算隐藏层和输出层。

举个例子，上图为4层神经网络，隐藏层数量为3，隐藏层单元数量为5，5，3，一个输出层。

💡一些记号

L：表示神经网络的总层数
$n^{[l]}$ ：表示l层上的单元数（节点数）

还是以上图4层神经网络为例，L=4， $n^{[1]}$ =5（表示第一个隐藏层单元数为5），类似的 $n^{[2]}=5$ ， $n^{[3]}=3$ ， $n^{[4]}=1$ ，对于输入层 $n^{[0]}=n_x=3$ （表示3个输入特征x1,x2,x3）。

对于第l层，用 $a^{[l]}$ 表示l层的激活函数输出，由 $a^{[l]}=g(z^{[l]})$ 计算得到。用 $W^{[l]}$ 来表示在 $a^{[l]}$ 中计算z^[l]值的权重， $b^{[l]}$ 也一样。输入特征用x表示，x也是第0层的激活函数，所以 $x=a^{[0]}$ 。最后一层的激活函数 $a^{[L]}=\hat{y}$ （预测输出）。

4.2 深层网络中的前向传播

先来看对其中一个训练样本x如何应用前向传播。

第 1 层：

$z^{[1]}=W^{[1]}x+b^{[1]}$

$a^{[1]}=g^{[1]}(z^{[1]})$

第 2 层

$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$

$a^{[2]}=g^{[2]}(z^{[2]})$

第 3 层

$z^{[3]}=W^{[3]}a^{[2]}+b^{[3]}$

$a^{[3]}=g^{[3]}(z^{[3]})$

......

以此类推第 l 层：

$z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$

$a^{[l]}=g^{[l]}(z^{[l]})$

📜总结：

（1）对于第l层，其正向传播中的步骤可以写成：

$z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$

$a^{[l]}=g^{[l]}(z^{[l]})$

（2）向量化实现过程可以表示为：

$z^{[l]}=W^{[l]}\cdot A^{[l-1]}+b^{[l]}$

$a^{[l]}=g^{[l]}(z^{[l]})$

4.3 核对矩阵的维数

本小节提供了一种个检查代码是否有错的方法，即“核对一遍算法中矩阵的维数” 。

接下来，提供了标注各个变量维数的方法：

w的维度是（当前层的维数，前一层的维数），即 $W^{[l]}:(n^{[l]},n^{[l-1]})$

b的维度是（当前层的维数，1），即 $b^{[l]}:(n^{[l]},1)$

z和a的维度相同，即 $z^{[l]},a^{[l]}:(n^{[l]},1)$

dw和w维度相同，db和b维度相同，且w和b向量化维度不变，z,a和x会变，它们由训练集大小决定。

进行向量化后， $Z^{[l]},A^{[l]}:(n^{[l]},m),A^{[0]}=X=(n^{[l]},m)$

4.4 为什么使用深层表示

以面部识别场景为例，来看神经网络如何进行应用。

在这个例子中，创建一个大概有20个隐藏单元的深度神经网络，分析如何针对这张图进行计算。

（1）藏单元就是这些图里这些小方块，我们可以把照片里组成边缘的像素们放在一起看。

（2）然后它可以把被探测到的边缘组合成面部的不同部分，比如说，可能有一个神经元会去找眼镜，另外还有别的找鼻子的部分，然后把这许多的边缘结合在一起，就可以开始检测人脸的不同部分。

（3）最后再把这些部分放在一起，比如眼睛鼻子下巴，就可以识别或探测不同的人脸了。

这种可视化的一个技术细节，边缘探测器相对来说都是针对照片中非常小块的面积，面部探测器呢就会针对大一些的区域，但是主要的概念是一般从小的细节人手（比如边缘），然后再一步步到更大更复杂的区域。

如果想建立一个语音识别系统时，需要解决如何可视化语音，比如输入一个音频片段，那么神经网络的第一层可能先开始试着探测比较低层次的音频波形的一些特征，比如音调的高低、分辨白噪声等，然后把这些波形组合在一起，就能去探测声音的基本单元。在语言学中有个概念叫音位（phonemes），像cat中c-a-t都是音位，有了基本声音单元，组合起来就能识别音频中的单词。

4.5 搭建深层神经网络块

这是一个层数较少的神经网络，从这一层的计算入手。下面用流程块图来解释神经网络正向传播和反向传播过程。如下图所示，对于第l层来说，正向传播过程中

下面看正向传播和反向传播的流程：

4.6 正向和反向传播

正向传播（forward propagation）：输入 $a^{[l-1]}$ ，输出 $a^{[l]}$ ，缓存变量是 $z^{[l]}$ ；从实现的角度来说我们可以缓存下 $w^{[l]}$ 和 $b^{[l]}$ ，这样更容易在不同的环节中调用函数。

所以正向传播的步骤可以写成：

$z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$

$a^{[l]}=g^{[l]}(z^{[l]})$

m个训练样本，向量化实现过程为：

$z^{[l]}=W^{[l]}\cdot A^{[l-1]}+b^{[l]}$

$A^{[l]}=g^{[l]}(z^{[l]})$

下面讲反向传播（backward propagation）：输入 $da^{[l]}$ ，输出是 $da^{[l-1]},dw^{[l]},db^{[l]}$ 。

反向传播的步骤如下：

（1） $dz^{[l]}=da^{[l]}\ast g^{[l]}(z^{(l)})$

（2） $dw^{[l]}=dz^{(l)}\cdot a^{[l-1]}$

（3） $db^{[l]}=dz^{(l)}$

（4） $da^{[l-1]}=w^{[l]T}\cdot dz^{[l]}$

（5） $dz^{[l]}=w^{[l+1]T}dz^{[l+1]}\cdot g^{[l]}(z^{[l]})$

式子（5）由式子（4）带入式子（1）得到，前四个式子就可实现反向函数。

向量化实现过程可以写成：

（1） $dZ^{[l]}=dA^{[l]}\ast g^{[l]}(Z^{(l)})$

（2） $dW^{[l]}=\frac{1}{m}dZ^{(l)}\cdot A^{[l-1]T}$

（3） $db^{[l]}=\frac{1}{m}np.sum(dz^{(l)},axis=1,keepdims=True)$

（4） $dA^{[l-1]}=W^{[l]T}\cdot dZ^{[l]}$

🙋反向传播中如何初始化？

$da^{[l]}=-\frac{y}{a}+\frac{1-y}{1-a}$

$dA^{[l]}=(-\frac{y^{[1]}}{a^{[1]}}+-\frac{1-y^{[1]}}{1-a^{[1]}}...-\frac{y^{[m]}}{a^{[m]}}+-\frac{1-y^{[m]}}{1-a^{[m]}})$

4.7 参数 VS 超参数

想要神经网络有很好的效果，还需要规划好你的参数以及超参数。

比如算法中的learning rate α（学习率）、iterations N(梯度下降法循环的数量)、L（神经网络层数）、 $n^{[l]}$ （各层的神经单元数目）、choice of activation function（激活函数的选择）都需要设置，这些数字实际上控制了最后的参数W和b的值，所以被称作超参数（hyperparameters）。

实际上深度学习有很多不同的超参数，之后也会讲一些其他的超参数，比如momentum，mini batch的大小，几种不同的正则化参数（regularization parameters）等（这些参数会在跟着吴恩达学深度学习（二）提及）。

🙋如何寻找超参数的最优值？

走Idea—Code—Experiment—Idea这个循环，尝试各种不同的参数，实现模型并观察是否成功，然后再迭代。根据经验我们选取了学习率=0.01，但是在开发新的应用时，很难预先确切知道究竟超参数的最优值是什么，所以通常需要尝试不同的值，并走上面的循环，试试各种参数。

4.8 这和大脑有什么关系？

🙋神经网络跟人脑机制到底有什么联系呢？究竟有多少的相似程度？

其实关联性不大。当你在实现一个神经网络的时候，那些公式是你在做的东西，你会做前向传播、反向传播、梯度下降法，其实很难表述这些公式具体做了什么，深度学习像大脑这样的类比其实是过度简化了我们的大脑具体在做什么，但因为这种形式很简洁，也能让普通人更愿意公开讨论，也方便新闻报道并且吸引大众眼球，但这个类比是非常不准确的。

一个神经网络的逻辑单元可以看成是对一个生物神经元的过度简化，但它是极其复杂的，单个神经元到底在做什么目前还没有人能够真正可以解释。

这个类比还是很粗略的，人脑神经元可分为树突、细胞体、轴突三部分。树突接收外界电刺激信号（类比神经网络中神经元输入），传递给细胞体进行处理（类比神经网络中神经元激活函数运算），最后由轴突传递给下一个神经元（类比神经网络中神经元输出）。这是一个过度简化的对比，把一个神经网络的逻辑单元和右边的生物神经元对比。