1.图像去噪的前言
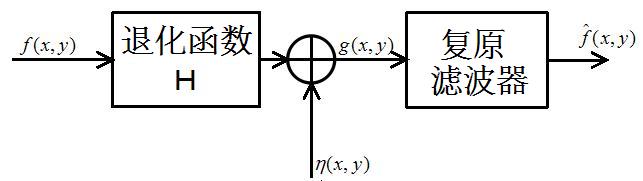
上一篇博文中,我对噪声的类型进行了介绍,也使用的Matlab对各种噪声进行了实现。旧话重提,一幅图像,甚至是一个信号的老化,可以使用以下模型来表示。
可以使用以下算式来表示
这里,由于退化函数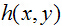
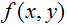
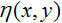
本博文,主要对去除加性噪声的线性滤波器的性能进行了比较。对于退化函数的去除(称为去卷积或者逆滤波),将放在稍后的博文。
1.1 实验用图像
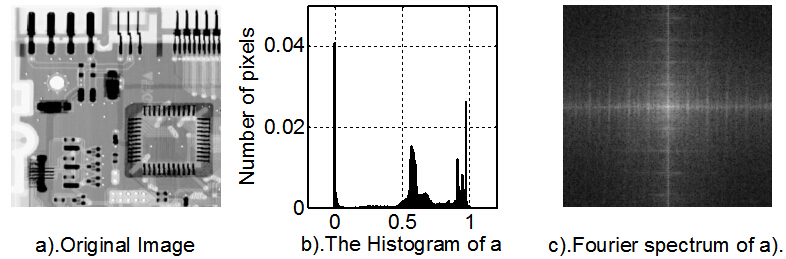
1.2 实验结果的评价
实验的步骤为,将实验用图像加上加性噪声,然后使用滤波器进行去噪,比较所得到的图像的画质。这里,就涉及到画质的评价方法。一般的,去噪图像的评价一般使用PSNR(峰值信噪比)。
对于8-bit的图片而言,这里的MAX为255。PSNR越大,其画质就越好。但是,有些时候,使用PSNR来进行评价,也有不太合理的时候。
请对比如下三张图片,a)是使用平均滤波器进行了处理,使其有些模糊;b)是使用高斯噪声污染原图;c)是使用椒盐噪声污染的图像。
问题来了,这三张图像哪张画质最好,哪张最差。普遍的,画质从好到差排列,大家的答案应该是
a) > c) > b)
这样的(更多实际例子,请参考https://ece.uwaterloo.ca/~z70wang/research/ssim/)。那么,我们求其的PSNR是这样的。
这明显不科学,三幅图像的PSNR是一样的。反观PSNR的计算式,PSNR计算的时候,使用了MSE这个量。而MSE仅仅表现了两幅图像的灰度值的差,而对于图像的结构,却没有进行任何分析。
这里使用一种比较好的图像画质评价的方法:SSIM(念做:艾斯-希姆)。这是一种由两张图像的灰度差异,构造差异和对比度去判断两张图的接近程度的方法。详情请参考[文献1],这里只做简单的介绍一下啦。
SSIM从图像亮度(Luminance),图像对比度(Contrast)和图像构造(Structure)去判断处理过的图像与原图的差异。这里,使用了某个区域的内的平均值作为亮度度量,使用方差作为对比度度量,使用协方差作为构造度量,来进行判断。这样,SSIM就比仅使用灰度去判断的PSNR更加准确。一样的,使用SSIM求取上面三幅图象的类似度。
从上表可以看出来,通过使用SSIM进行判断的结果,更加符合人眼的主观感受。本文余下的实验,全部使用SSIM去判断画质。








 本文探讨了图像去噪中的线性处理,重点比较了几种均值滤波器,包括算术均值、几何均值、谐波均值和逆谐波均值滤波器。通过实验和SSIM指数分析,揭示了这些滤波器在去除加性噪声时的效果,指出SSIM作为评价标准更能准确反映图像质量。
本文探讨了图像去噪中的线性处理,重点比较了几种均值滤波器,包括算术均值、几何均值、谐波均值和逆谐波均值滤波器。通过实验和SSIM指数分析,揭示了这些滤波器在去除加性噪声时的效果,指出SSIM作为评价标准更能准确反映图像质量。
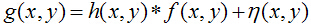
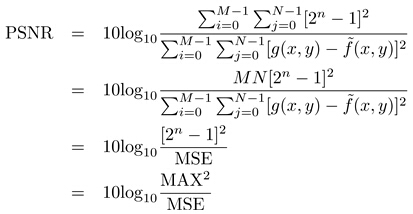


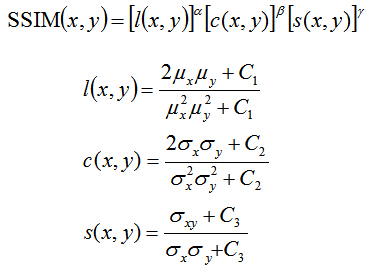

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 7572
7572

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








