Linux&Shell9.5作业

栈与队列知识点总结

栈（Stack）

1. 基本概念

定义：只能在同一端（栈顶）进行插入或删除操作的线性表
栈顶（top）：允许进行插入、删除操作的一端
栈底（bottom）：不允许操作的另一端
特点：后进先出（LIFO）或先进后出

2. 基本操作

push(e)：进栈/入栈，将元素e插入到栈顶
pop()：出栈/退栈，移除并返回栈顶元素
gettop()：取栈顶元素（不移除）
empty()：判断栈是否为空

3. 应用场景

函数调用栈
表达式求值
括号匹配
浏览器前进后退

队列（Queue）

1. 基本概念

定义：只能在不同端进行插入或删除操作的线性表
队头（front）：进行删除操作的一端
队尾（rear）：进行插入操作的一端
特点：先进先出（FIFO）

2. 基本操作

push(e)：入队，将元素e插入到队尾
pop()：出队，从队头移除元素
gethead()：取队头元素（不移除）
empty()：判断队列是否为空

3. 队列类型

（1）非循环队列

初始化：front = rear = -1
队空条件：front == rear
队满条件：rear == MaxSize-1
缺点：存在"假溢出"问题

（2）循环队列（推荐）

初始化：front = rear = 0
队空条件：rear == front
队满条件：(rear + 1) % MaxSize == front
优点：解决假溢出问题，充分利用空间

总结

1. 栈：LIFO，单端操作，常用于反转顺序、匹配问题
2. 队列：FIFO，双端操作，常用于按顺序处理、广度优先搜索
3. 循环队列：解决假溢出，空间利用率高
4. 相互实现：
   栈→队列：需要两个栈（输入栈+输出栈）
   队列→栈：需要旋转操作（单队列或双队列）

复杂度分析

操作 栈 队列 栈实现队列 队列实现栈
push O(1) O(1) O(1) O(n)
pop O(1) O(1) 均摊O(1) O(1)
peek O(1) O(1) 均摊O(1) O(1)

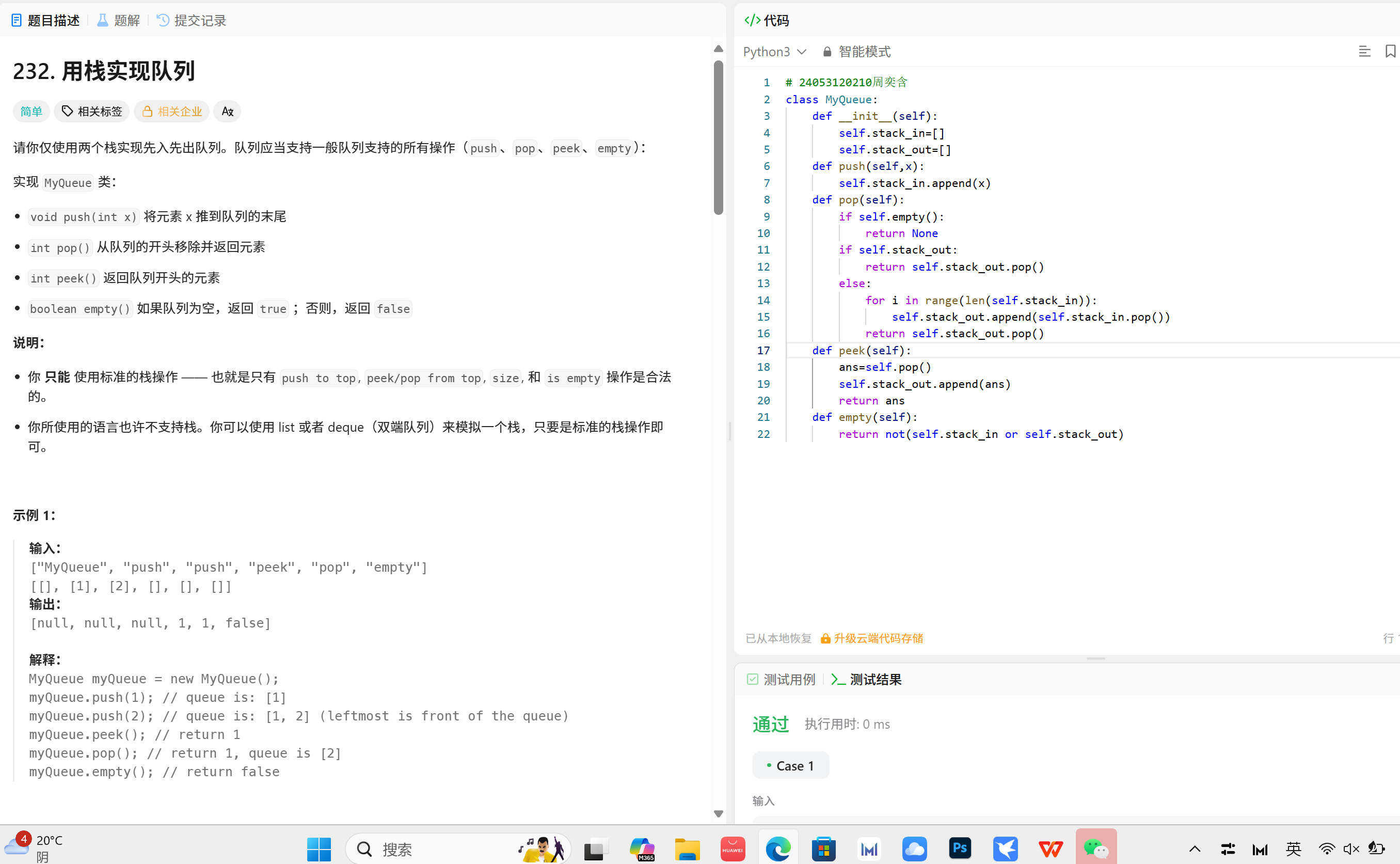
LeetCode232解题思路（用栈实现队列）：

使用两个栈：inputStack（用于压入新元素）和 outputStack（用于弹出和查看队首元素）。
当需要弹出（pop）或查看队首（peek）时：
如果 outputStack 为空，则将 inputStack 中的所有元素弹出并压入 outputStack（这样顺序就被反转了，最先进入的元素在 outputStack 的顶部）。
如果 outputStack 不为空，则直接操作 outputStack 的栈顶。
压入（push）操作直接压入 inputStack。
判断空（empty）时，需要同时检查两个栈是否都为空。

步骤：

1. 初始化两个栈。
2. push(x): 直接压入 inputStack。
3. pop(): 如果 outputStack 为空，则将 inputStack 的所有元素弹出并压入 outputStack，然后弹出 outputStack 的栈顶；否则直接弹出 outputStack 的栈顶。
4. peek(): 类似 pop()，但不移除元素。
5. empty(): 当两个栈都为空时返回 true，否则 false。

复杂度：

push 操作：O(1)
pop/peek 操作：均摊 O(1)（因为每个元素最多被压入和弹出两次）

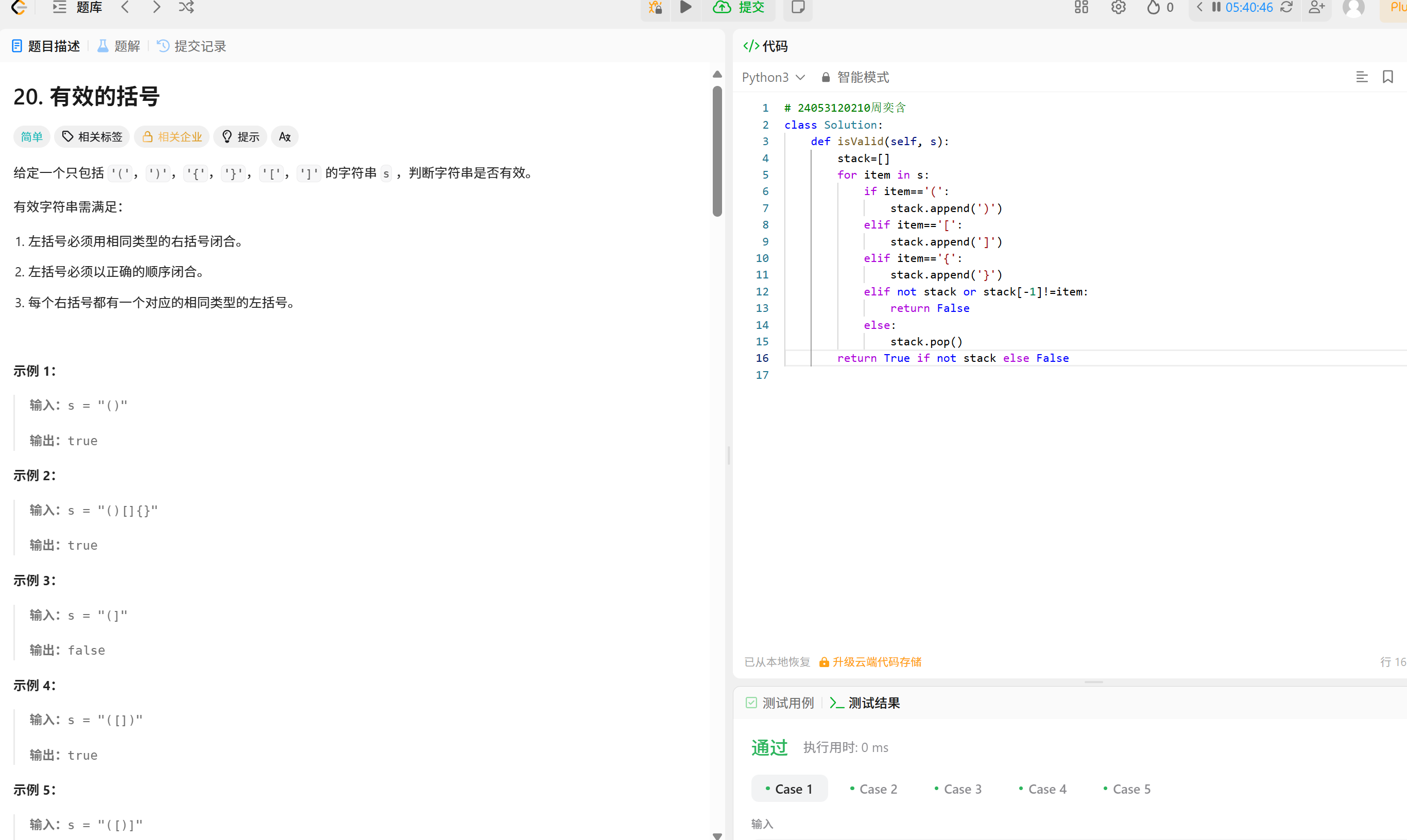
LeetCode20解题思路（有效的括号）：

使用栈来跟踪未匹配的左括号。
遍历字符串：
遇到左括号（'(', '[', '{'）时，压入栈。
遇到右括号（')', ']', '}'）时，检查栈顶是否是对应的左括号：
如果是，弹出栈顶（表示匹配成功）。
如果不是（或栈为空），则无效。
最后，如果栈为空（所有左括号都被匹配），则有效；否则无效。

步骤：

1. 初始化一个栈。
2. 遍历每个字符：
 如果是左括号，压入栈。
 如果是右括号：
 如果栈为空，返回 false（没有左括号匹配）。
 检查栈顶是否与当前右括号匹配（即：'(' 与 ')'，'[' 与 ']'，'{' 与 '}'），如果匹配则弹出栈顶，否则返回 false。
3. 遍历结束后，如果栈为空则返回 true，否则返回 false。

注意：

可以使用哈希表存储括号的对应关系（键为右括号，值为左括号），以便快速检查。
提前判断字符串长度是否为偶数（奇数一定无效）可优化。

复杂度：

时间：O(n)（遍历一次字符串）
空间：O(n)（栈的空间）

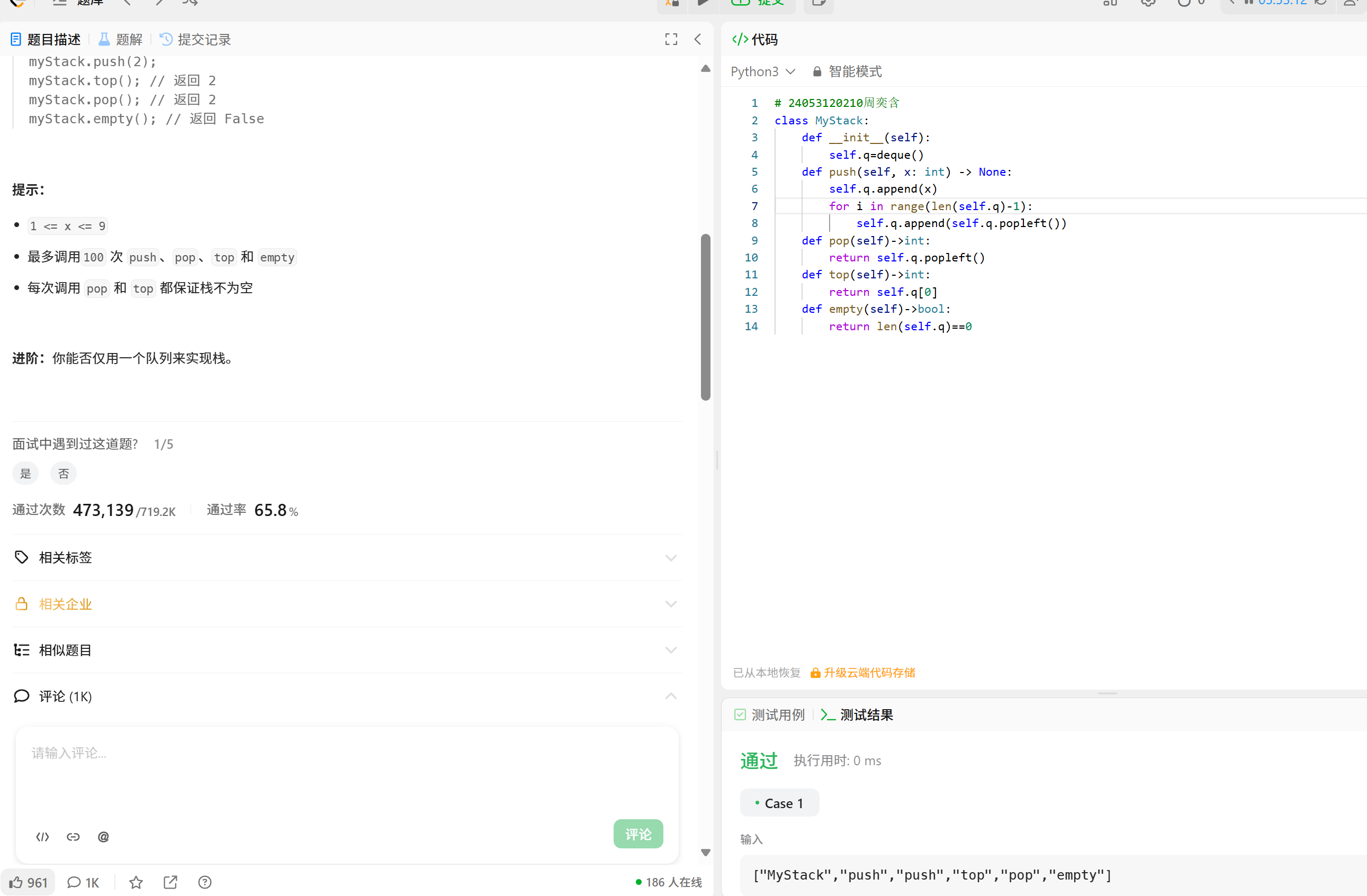
LeetCode225解题思路（单队列）：

push(x)：将新元素x压入队列，然后将队列中除了新元素外的所有元素依次出队并重新入队（循环n-1次）。
这样新元素就会移动到队列前端（成为栈顶）。
pop()：直接出队。
top()：返回队列前端元素。
empty()：检查队列是否为空。

复杂度分析

push操作：O(n)（需要移动n-1个元素）
pop/top/empty操作：O(1)

代码解释

1. 初始化：使用deque模拟队列。
2. push(x)：
   先将新元素x入队。
   然后将队列中除x外的所有元素（即前n-1个元素）依次出队并重新入队。
   这样x就成为了队列的第一个元素（即栈顶）。
3. pop()：直接出队队列的第一个元素（即栈顶）。
4. top()：返回队列的第一个元素（即栈顶）。
5. empty()：检查队列是否为空。

这种方法保证了：

每次push后，新元素都在队列前端
pop和top操作直接访问队列前端元素
完全符合栈的LIFO特性