【人工智能】深入探索Python-NumPy库：一文带你了解NumPy人工智能中的应用

在当今数据驱动的世界里，NumPy 已成为Python数据科学领域的基石。无论是数据分析、机器学习，还是科学计算，NumPy都以其高效的数值计算能力和丰富的功能，成为开发者和数据科学家们的首选工具。那么，NumPy究竟有多强大？如何充分利用它的潜力？本文将带你全面了解这一强大库，并通过详细的教程，助你快速掌握NumPy的使用技巧。

🌟为什么选择NumPy？揭开其在数据科学中的核心地位

在Python生态系统中，NumPy以其独特的优势，占据了数值计算领域的核心位置。以下几点充分展示了其不可替代的价值：

1. 高性能的多维数组对象（ndarray）：NumPy的ndarray对象不仅提供了高效的内存使用，还支持快速的向量化运算，这在处理大规模数据时尤为重要。
2. 丰富的数学函数库：NumPy内置了大量的数学函数，涵盖了基本的算术运算、线性代数、傅里叶变换等，为复杂计算提供了便捷的工具。
3. 强大的广播机制：广播机制允许不同形状的数组在运算时自动调整尺寸，极大地简化了代码编写，提高了计算效率。
4. 与其他库的无缝集成：NumPy与Pandas、Matplotlib、SciPy等数据科学库高度兼容，构建了一个功能强大的数据分析生态系统。
5. 支持C/C++和Fortran的集成：通过与低级语言的接口，NumPy能够利用它们的优化性能，进一步提升计算速度。

这些优势使得NumPy不仅在学术研究中广泛应用，也在工业界的数据处理和分析中扮演着重要角色。

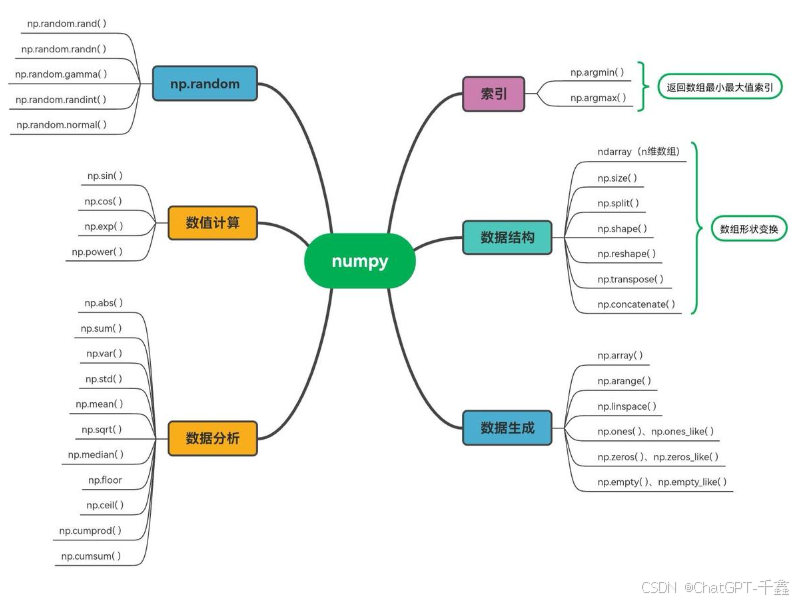
📚NumPy全面教程：从基础到高级，轻松掌握数值计算

为了帮助你全面掌握NumPy，本文将从基础概念开始，逐步深入到高级功能，通过实际示例解析其应用。

ChatGPT中文版可以在这里体验：ChatMoss & ChatGPT中文版

1. NumPy简介与安装

1.1 什么是NumPy？

NumPy，即“Numerical Python”，是Python的一个开源数值计算扩展库，提供了高效的多维数组对象、丰富的数学函数和强大的数据操作工具。它是构建其他数值计算库（如Pandas、SciPy）的基础。

1.2 安装NumPy

在开始使用NumPy之前，需要确保其已安装在你的Python环境中。以下是在不同环境下安装NumPy的方法：

• 使用pip安装：

  pip install numpy
  

• 使用conda安装（适用于Anaconda用户）：

  conda install numpy
  

安装完成后，可以通过以下命令验证安装成功：

import numpy as np
print(np.__version__)

2. NumPy核心：ndarray多维数组对象

2.1 创建ndarray

ndarray是NumPy的核心，是一个多维数组对象，用于存储同类型的数据。以下是创建ndarray的几种常用方法：

• 通过Python列表创建：

  import numpy as np
  
  # 创建一维数组
  a = np.array([1, 2, 3, 4, 5])
  print(a)
  
  # 创建二维数组
  b = np.array([[1, 2, 3], [4, 5, 6]])
  print(b)
  

• 使用内置函数创建：

  # 创建全零数组
  zeros = np.zeros((3, 4))
  print(zeros)
  
  # 创建全一数组
  ones = np.ones((2, 3))
  print(ones)
  
  # 创建单位矩阵
  eye = np.eye(3)
  print(eye)
  
  # 创建等差数组
  arange = np.arange(0, 10, 2)
  print(arange)
  
  # 创建等间隔数组
  linspace = np.linspace(0, 1, 5)
  print(linspace)
  

2.2 ndarray属性

ndarray对象拥有多个属性，帮助我们了解数组的结构和内容：

• shape：数组的维度
• dtype：数组元素的数据类型
• size：数组元素的总数量
• ndim：数组的维数

a = np.array([[1, 2, 3], [4, 5, 6]])
print("Shape:", a.shape)
print("Data type:", a.dtype)
print("Size:", a.size)
print("Number of dimensions:", a.ndim)

2.3 数组索引与切片

与Python列表类似，NumPy数组支持索引和切片，但功能更强大：

• 一维数组索引与切片：

  a = np.array([10, 20, 30, 40, 50])
  
  # 获取第一个元素
  print(a[0])  # 输出：10
  
  # 获取前3个元素
  print(a[:3])  # 输出：[10 20 30]
  
  # 步长切片
  print(a[::2])  # 输出：[10 30 50]
  

• 二维数组索引与切片：

  b = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
  
  # 获取特定元素
  print(b[1, 2])  # 输出：6
  
  # 获取第二行
  print(b[1, :])  # 输出：[4 5 6]
  
  # 获取第一列
  print(b[:, 0])  # 输出：[1 4 7]
  
  # 切片获取子数组
  print(b[:2, 1:3])  
  # 输出：
  # [[2 3]
  #  [5 6]]
  

3. 通用函数（ufuncs）与向量化运算

NumPy的核心优势之一是其支持向量化运算，通过通用函数（ufuncs）实现高效的批量操作，无需显式的Python循环。

体验最新GPT-o1模型：ChatMoss & ChatGPT中文版

3.1 基本运算

a = np.array([1, 2, 3, 4])
b = np.array([10, 20, 30, 40])

# 加法
print(a + b)  # 输出：[11 22 33 44]

# 乘法
print(a * b)  # 输出：[10 40 90 160]

3.2 广播机制

广播允许不同形状的数组进行运算，NumPy会自动调整较小数组的形状以匹配较大数组。

a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([10, 20, 30])

# 广播加法
print(a + b)
# 输出：
# [[11 22 33]
#  [14 25 36]]

3.3 常用通用函数

• 数学函数：

  a = np.array([0, np.pi/2, np.pi])
  
  print(np.sin(a))  # 输出：[0.000000e+00 1.000000e+00 1.224647e-16]
  print(np.cos(a))  # 输出：[ 1.000000e+00  6.123234e-17 -1.000000e+00]
  

• 统计函数：

  data = np.array([1, 2, 3, 4, 5])
  
  print(np.mean(data))  # 输出：3.0
  print(np.std(data))   # 输出：1.4142135623730951
  print(np.sum(data))   # 输出：15
  

4. 高级功能

NumPy不仅提供基础的数组操作，还包含许多高级功能，助力复杂的数值计算。

4.1 线性代数

NumPy的linalg模块提供了强大的线性代数函数，包括矩阵乘法、求逆、特征值计算等。

from numpy.linalg import inv, eig

A = np.array([[1, 2], [3, 4]])

# 矩阵乘法
B = np.array([[5, 6], [7, 8]])
C = np.dot(A, B)
print(C)
# 输出：
# [[19 22]
#  [43 50]]

# 矩阵求逆
A_inv = inv(A)
print(A_inv)
# 输出：
# [[-2.   1. ]
#  [ 1.5 -0.5]]

# 特征值和特征向量
values, vectors = eig(A)
print("Eigenvalues:", values)
print("Eigenvectors:\n", vectors)

4.2 随机数生成

NumPy的random模块提供了丰富的随机数生成函数，适用于模拟和统计分析。

from numpy.random import rand, randint, normal

# 均匀分布随机数
uniform_random = rand(3, 2)
print(uniform_random)

# 整数随机数
int_random = randint(1, 10, size=(2, 3))
print(int_random)

# 正态分布随机数
normal_random = normal(loc=0.0, scale=1.0, size=5)
print(normal_random)

4.3 傅里叶变换

傅里叶变换在信号处理、频谱分析等领域有广泛应用，NumPy提供了相关函数简化操作。

from numpy.fft import fft, ifft

# 创建一个信号
t = np.linspace(0, 1, 400)
signal = np.sin(2 * np.pi * 50 * t) + np.sin(2 * np.pi * 120 * t)

# 计算傅里叶变换
signal_fft = fft(signal)

# 计算逆傅里叶变换
signal_ifft = ifft(signal_fft)

print("Original Signal:", signal[:10])
print("FFT:", signal_fft[:10])
print("Reconstructed Signal:", signal_ifft[:10].real)

5. 文件I/O操作

NumPy提供了便捷的文件读写函数，支持多种数据格式，方便数据的持久化和交换。

# 保存数组到二进制文件
np.save('array.npy', a)

# 从二进制文件加载数组
loaded_a = np.load('array.npy')
print(loaded_a)

# 保存数组到文本文件
np.savetxt('array.txt', a, delimiter=',')

# 从文本文件加载数组
loaded_txt_a = np.loadtxt('array.txt', delimiter=',')
print(loaded_txt_a)

6. 与Pandas和Matplotlib的协同使用

NumPy与Pandas、Matplotlib等库的无缝集成，使数据处理和可视化更加高效便捷。

import pandas as pd
import matplotlib.pyplot as plt

# 创建NumPy数组
data = np.random.randn(1000)

# 使用Pandas进行数据分析
df = pd.DataFrame(data, columns=['Value'])
print(df.describe())

# 使用Matplotlib进行数据可视化
df.hist(bins=30)
plt.show()

🚀提升性能：NumPy高效编程技巧

掌握NumPy不仅仅是了解其功能，更在于如何高效地使用它。以下是一些提升性能的实用技巧：

体验最新GPT-o1模型：ChatMoss & ChatGPT中文版

1. 避免显式循环

尽量使用NumPy的向量化运算，避免使用Python的显式循环，因为后者在处理大规模数据时效率低下。

# 不推荐的做法
result = []
for x in a:
    result.append(x * 2)

# 推荐的做法
result = a * 2

2. 使用内置函数

NumPy的内置函数经过高度优化，性能远超自定义的Python函数。

# 自定义函数
def square(x):
    return x ** 2

result = np.array([square(x) for x in a])

# 使用NumPy内置函数
result = np.square(a)

3. 内存管理

了解和优化内存使用可以显著提升程序性能，特别是在处理大规模数据时。

# 使用合适的数据类型
a = np.array([1, 2, 3], dtype=np.float32)  # 占用内存更少

# 使用共享内存或内存映射
large_array = np.memmap('large_array.dat', dtype='float32', mode='w+', shape=(10000, 10000))

4. 并行计算

虽然NumPy本身并不直接支持并行计算，但可以结合其他工具（如Numba、Cython）实现更高的性能。

from numba import njit

@njit
def fast_sum(a):
    total = 0
    for x in a:
        total += x
    return total

print(fast_sum(a))

🔍实战案例：使用NumPy进行数据分析

为了更好地理解NumPy的应用，以下通过一个实际案例，展示如何使用NumPy进行数据分析。

案例描述

假设我们有一组销售数据，包含日期和销售额。我们需要分析销售趋势、计算移动平均，并进行预测。

1. 数据准备

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# 生成日期
dates = pd.date_range(start='2023-01-01', periods=100)

# 生成随机销售额数据
sales = np.random.randint(100, 500, size=100)

# 创建DataFrame
df = pd.DataFrame({'Date': dates, 'Sales': sales})
print(df.head())

2. 数据分析

• 计算基本统计量

mean_sales = np.mean(sales)
std_sales = np.std(sales)
print(f"平均销售额: {mean_sales}")
print(f"销售额标准差: {std_sales}")

• 计算移动平均

window_size = 7
moving_avg = np.convolve(sales, np.ones(window_size)/window_size, mode='valid')

# 添加到DataFrame
df['Moving_Avg'] = np.nan
df['Moving_Avg'].iloc[window_size-1:] = moving_avg
print(df.head(10))

3. 数据可视化

plt.figure(figsize=(12, 6))
plt.plot(df['Date'], df['Sales'], label='每日销售额')
plt.plot(df['Date'], df['Moving_Avg'], label='7天移动平均', color='red')
plt.xlabel('日期')
plt.ylabel('销售额')
plt.title('销售趋势分析')
plt.legend()
plt.show()

4. 销售预测（简单线性回归）

from sklearn.linear_model import LinearRegression

# 准备数据
X = np.arange(len(sales)).reshape(-1, 1)
y = sales

# 创建并训练模型
model = LinearRegression()
model.fit(X, y)

# 预测未来10天的销售额
X_future = np.arange(len(sales), len(sales)+10).reshape(-1,1)
y_pred = model.predict(X_future)

# 可视化预测结果
future_dates = pd.date_range(start=dates[-1] + pd.Timedelta(days=1), periods=10)
plt.figure(figsize=(12, 6))
plt.plot(df['Date'], df['Sales'], label='历史销售额')
plt.plot(future_dates, y_pred, label='预测销售额', color='green')
plt.xlabel('日期')
plt.ylabel('销售额')
plt.title('销售预测')
plt.legend()
plt.show()

更多文章

【IDER、PyCharm】免费AI编程工具完整教程：ChatGPT Free - Support Key call AI GPT-o1 Claude3.5

【OpenAI】获取OpenAI API KEY的两种方式，开发者必看全方面教程！

【Cursor】揭秘Cursor：如何免费无限使用这款AI编程神器？

🏅总结

NumPy 作为Python数据科学领域的基石，其高效的数值计算能力和丰富的功能，使其在数据分析、机器学习、科学计算等多个领域发挥着重要作用。通过本文的全面介绍和详细教程，相信你已经对NumPy有了深入的了解，并掌握了其基本用法和高级技巧。

无论你是刚入门的数据科学新手，还是经验丰富的开发者，掌握NumPy都将为你的数据处理和分析工作带来极大的便利和提升。持续学习和实践，探索NumPy的更多功能，你将发现这一工具无穷的可能性！