1. 指数衰减过程
在计算诸如新闻热度、特征重要度等场合下,我们需要一种具有这样特性的过程,一个数值随着时间的推移呈现指数形式逐渐放缓的衰减,即这个数值的衰减速度和当前值成正比,数学公式为
dNdt=−αN
d
N
d
t
=
−
α
N
其中 α>0 α > 0 称为指数衰减常数。通过解微分方程可得
N(t)=N0e−αt(1)
N
(
t
)
=
N
0
e
−
α
t
(
1
)
其中 N(t) N ( t ) 为 N N 在时刻的数值, N0=N(0) N 0 = N ( 0 ) 为 N N 在时刻的初始数值,也是当 t≥0 t ≥ 0 的最大值。举例来说,一篇新闻的初始热度为 N0 N 0 ,那么随着时间的推移其热度按照指数形式的下降,计算公式就是式(1)。假设 N0=1 N 0 = 1 ,那么该新闻的热度随时间变化如下图所示,该新闻在第30天时热度趋近于0.

2. 更进一步控制衰减过程
以上公式仅仅表示数值可以按照指数形式进行衰减,但是往往需要更精细的控制衰减过程,比如该数值从多大的数值继续衰减,再经过多长时间的衰减后,下降到多大的数值等等,这就需要略微修改计算公式为
N(t)=N0e−α(t+l)(2)
N
(
t
)
=
N
0
e
−
α
(
t
+
l
)
(
2
)
其中 l l 表示向左的平移量,它可以让数值不必从开始衰减,而从任何位置处继续衰减。假设我们需要从 Ninit N i n i t 处继续衰减,经过 m m 天衰减到,列写方程为
N0e−αl=NinitN0e−α(m+l)=Nfinish
N
0
e
−
α
l
=
N
i
n
i
t
N
0
e
−
α
(
m
+
l
)
=
N
f
i
n
i
s
h
可以解得
α=1mln(NinitNfinish)l=1αln(N0Ninit)
α
=
1
m
ln
(
N
i
n
i
t
N
f
i
n
i
s
h
)
l
=
1
α
ln
(
N
0
N
i
n
i
t
)
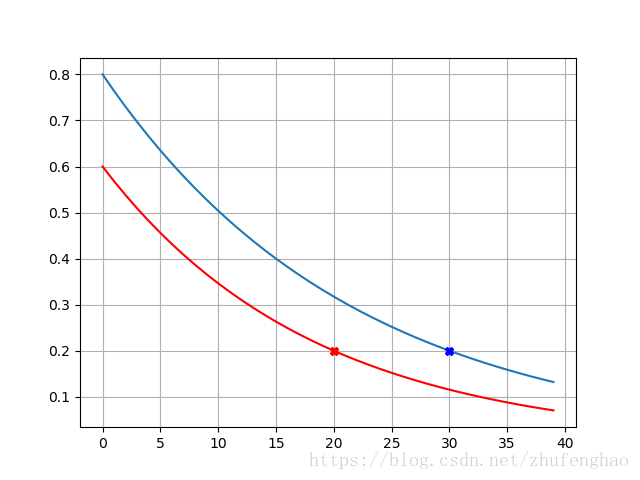
带入式(2)即可。这种精确受控的衰减过程可以通过举例说明。假设 N0=1 N 0 = 1 ,一个衰减过程 Ninit=0.8 N i n i t = 0.8 , m=30 m = 30 , Nfinish=0.2 N f i n i s h = 0.2 ,另一个衰减过程 Ninit=0.6 N i n i t = 0.6 , m=20 m = 20 , Nfinish=0.2 N f i n i s h = 0.2 ,则这两个过程随时间变化如下图所示,可以看到蓝线代表的衰减过程在有效时间内总是在红线之上,衰减的速率也要更小。
3. Python计算实现
实现的init、m和finish分别代表初始衰减值、衰减时间长度和完成衰减值。
import numpy as np
def exponential_decay(t, init=0.8, m=30, finish=0.2):
alpha = np.log(init / finish) / m
l = - np.log(init) / alpha
decay = np.exp(-alpha * (t + l))
return decay附参考
这是牛顿冷却定律及其应用
这是更详细的wiki定义,包括了控制衰减过程的一般方式(平均生命时长、半衰期)以及受两个或更多因素控制的衰减过程





















 1601
1601

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








