扇形的4个基本概念

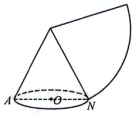
如图，要用一个扇形纸片围成一个无底盖的圆锥（接缝处忽略不计），若该圆锥的底面圆周长为8π cm，侧面积为72π平方厘米，则这歌扇形的圆心角的度数为（）

A 70度

B 80度【答案】

C 90度

D 100度

因为这是应用题而不是纯数学题，所以题中出现了这2个注意点：题中提到的【接缝处】指的是现实中想要围成圆锥总要消耗掉一点角度来涂抹胶水，长度带单位cm而不是单位一也是为了符合物理世界。当然这个不需要多说了，只是想聊聊应用题的存在意义。所有的数学应用题都可以转换成纯数学题，但是考试的时候总会出应用题，这多少有点政治意义在里面：任何理论都要结合实际。虽然说数学是被政治污染最少的学科，但是在老师将纯数学题转换成生活应用题的过程中难免会出现一些歧义或者不合理的地方。

回到这道题，扇形问题是几何题中的一个大类，但总体很简单，一个扇形包涵4个概念：圆心角、半径、弧长、面积。这4个概念之间可以相互转换，比如最直接的是：弧长=扇角*半径，当扇角=2π的时候就能推出圆周长=2πr。你看，本来2个公式在学生时代可能是分开来记忆的，现在将2者结合起来加深记忆，再也不怕忘记了。

这里要注意一下4个基本概念中，两个长度和一个面积都是直角坐标系中的单位，只有弧心角是极坐标系中的概念，关于宇宙的本质是圆的还是方的是一个非常深奥的问题，可能涉及到意识和物质的关系问题，所以我们不考虑那么多，只要知道这里弧心角的大小等于弧长和径长的比例，这个比例实际上消除了长度单位，将2个不同的坐标系联系起来了，也就是公理（显然易见的）。所以这里使用的是弧度制。

如何最直观的感受扇形的面积呢？并不是利用圆形面积公式乘以角度占比，而是将扇形微分成若干个三角形，把扇形想象成切好的西瓜，沿着中心再切成更小的西瓜。这就是微积分。

这张图是常见的用于形象理解圆形面积的方案，但是还是不够形象，还是扇形更好理解。因为扇形可以拆分成无数个三角形，这些三角形展开以后正好覆盖了一个矩形面积的一半。

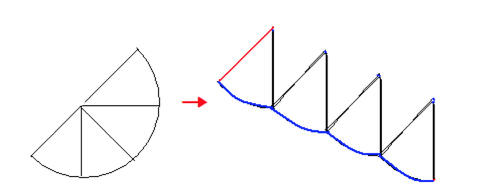
这样一来，是不是就直观地感受到扇形面积=底*高/2了？其中底就是弧长，高就是径长。最后利用这个公式来解决最开始的题目：