SVMの核函数

下面就网上流行的SVM教程中的错误部分给予说明：

http://www.blogjava.net/zhenandaci/archive/2009/02/13/254578.html

在上面的链接里就SVM的2次规划问题的得到给了详尽的解释，但是是错误的。

我先转引原文的解释：

在二元的线性分类中，这个表示分类的标记只有两个值，1和-1（用来表示属于还是不属于这个类）。有了这种表示法，我们就可以定义一个样本点到某个超平面的间隔：

δ_i=y_i(wx_i+b)

这个公式乍一看没什么神秘的，也说不出什么道理，只是个定义而已，但我们做做变换，就能看出一些有意思的东西。

首先注意到如果某个样本属于该类别的话，那么wx_i+b>0（记得么？这是因为我们所选的g(x)=wx+b就通过大于0还是小于0来判断分类），而y_i也大于0；若不属于该类别的话，那么wx_i+b<0，而y_i也小于0，这意味着y_i(wx_i+b)总是大于0的，而且它的值就等于|wx_i+b|！（也就是|g(x_i)|）

现在把w和b进行一下归一化，即用w/||w||和b/||w||分别代替原来的w和b，那么间隔就可以写成

这个公式是不是看上去有点眼熟？没错，这不就是解析几何中点x_i到直线g(x)=0的距离公式嘛！（推广一下，是到超平面g(x)=0的距离， g(x)=0就是上节中提到的分类超平面）

原文的问题出在哪里？

首先间隔δ_i=y_i(wx_i+b)，是错误的。间隔是直线与直线之间的，跟点没有关系。而后面的分析又完全建立在对点到直线距离的分析，完全和SVM本来的分析背道而驰。

实质上，要想理解如下二次规划问题并不难

Minimize (in )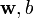

subject to (for any )

首先，我们看下这张图

我们要求的是平行直线H1和H2之间的最大间隔。

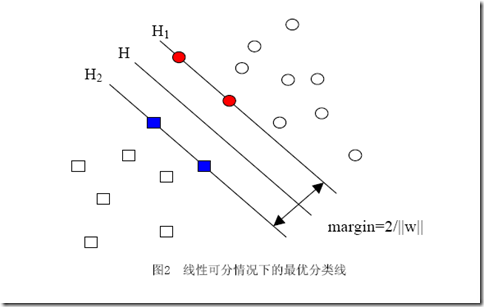
设H1: <w， x> + b1 =0;

H2: <w ，x> + b2 =0

尖括号是内积的意思，因为是平行直线，所以w相同。

注意这是直线表达式的一般形式。对于直线表达式的一般形式，两直线的距离公式如下

直线之间的间隔公式是：

|b1-b2|/||w||;

这里注意，b1,b2不是向量，是实数。要是向量是不能这么表示的。即使在超平面，b1,b2依然为实数，这点非常重要。这也是直线间距离公式在超平面依然成立的必要条件。

而w和x都是高维的向量。

下面对H1，H2正规化。怎么正规化？不是除以w，而是除以|b1-b2|，

这样H1: <w/|b1-b2| , x> +b1/|b1-b2|=0;

H2:<w/|b1-b2| , x> + b2/|b1-b2|=0;

这和原来的H1，H2是同样的两条直线。再令w'=w/|b1-b2|

所以，H1到H2的距离成为：

1/||w'||; 要距离最大，就是让||w'||最小。

以上是通过正规化换元在形式上的推导。我们更要问一下为什么，其实，有好多不同的直线表达式对应着相同的直线。系数成比例的直线表达式对应着相同的直线。我们必须把等比例系数的直线划归为一个表达式，这有点像我们从远处和近处观察同一个人，这人的鼻子始终是鼻子，虽然在远处看比较小，近处看比较大。于是我们控制住|b1-b2|的尺度，单独的考量直线间距离和||w||的关系，是一个完备的转换。不存在丢失解空间的问题。

然后看一下mercer定理：

首先介绍mercer定理：

对于所有2次可积的g(x)，K(x,y)满足

则K(x,y)可以作为核函数

至于为什么成立，暂时没有看懂原版证明。