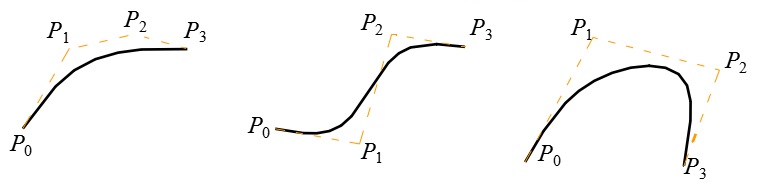
Bezier曲线的形状是通过一组多边折线(也称Bezier多边形或特征多边形)唯一定义出来的。
在多边折线的各顶点中,只有第一点和最后一点是在曲线上,其余顶点用来定义曲线的导数、阶次和形状。第一条边和最后一条边分别与曲线在起点和终点处相切。曲线形状趋于多边折线的形状。改变多边折线的顶点位置和曲线形状的变化有直观的联系。
Bezier曲线的数学表达式定义
n+1个顶点定义一个n次多项式,其参数向量表达式为:
式(4-21)中,Pi为各顶点的位置向量,Bi,n(t)为伯恩斯坦基函数,即Bezier多边形的各顶点位置向量之间的调和函数。该函数的表达式为:
若规定:00和0!均为1,则当 t=0时:
P(0) = P0B0, n(0) + P1B1,n(0) + P2B2, n(0) +…+ PnBn,n(0)
当t=0时,除第一项外其余各项均为0,即:
当t =1时:
当t =1时,除最后一项外其余各项均为0,即:
得出结论:Bezier曲线通过多边折线的起点和终点。
在起点t =0,式(4-25)中只有i=0, 1两项有效,即:

同理,在终点t =1,有:P'(1) = n(Pn-Pn-1) (4-27)
得出结论:Bezier曲线在点P0处与边P0P1相切,在点Pn处与边Pn-1Pn相切。
Bezier曲线的性质


Bezier曲线完全被包容在由特征多边形形成的凸包内。
几何不变性:
Bezier曲线的形状仅取决于特征多边形的顶点,而与坐标系的选取无关。
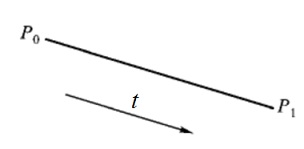
一次Bezier曲线
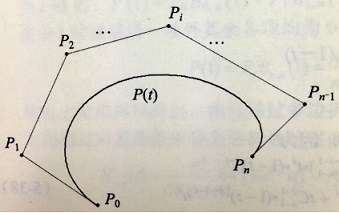
当n=1时,顶点 P0、P1可定义一条一次(n=1)Bezier曲线。此时式(4-21)可改写成:
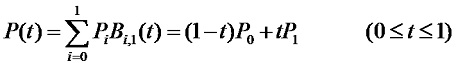
显然,一次Bezier曲线是一条点P0到点P1的直线段。
当n=2时,顶点P0、P1、P2可定义一条二次(n=2)Bezier曲线。此时式(4-21)可改写成:
P(t) = (1–t)2P0 + 2t(1–t)P1 + t2P2 (0≤t≤1) (4-28)
写成矩阵形式为:
二次Bezier曲线
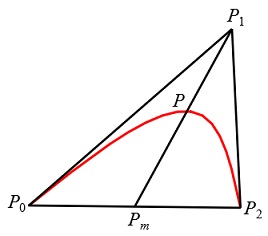
由式(4-28) ,二次Bezier曲线(n=2)在起点P0处有切向量P'0=P'(0)=2(P1–P0);在终点P2处有切向量P'2=P'(1) = 2(P2–P1)。同时,当t =1/2时:
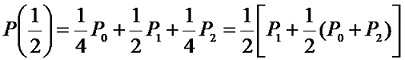
该式说明,二次Bezier曲线经过△P0P1P2中的一条中线P1Pm的中点P。并且可以看出二次Bezier曲线是一条抛物线。
三次Bezier曲线
当n=3时,顶点P0、P1、P2、P3四点可定义一条三次(n=3) Bezier曲线。此时式(4-21)可改写为:
P(t) = (1–t)3P0+3t(1–t)2P1+3t2(1–t)P2+t3P3
= (1–3t+3t2-t3)P0+ (3t–6t2+3t3)P1+ (3t2–3t3)P2 + t3P3 (0≤t≤1) (4-29)
写成矩阵表达式为:
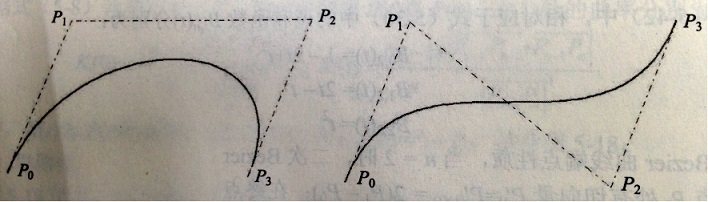
控制点相同但顺序不同的三次Bezier曲线
移动控制点P2的Bezier曲线的不同效果
Bezier曲线的控制顶点反求
已知Bezier曲线上给定参数处的位置矢量和参数阶次,利用Bezier曲线的定义和端点特性,可列出一组方程,求解方程组,可得到相应的控制顶点。
例如:已知三次Bezier曲线上的4个点分别为Q0(120, 0),Q1(45, 0),Q2(0, 45),Q3(0, 120), 它们对应的参数分别为0, 1/3,2/3,1,反求三次Bezier曲线的控制顶点。
由已知条件可得方程组:
Q0 = P0 (t=0)
Q1 = (8/27)P0 + (4/9)P1 + (2/9)P2 + (1/27)P3 (t=1/3)
Q2 = (1/27)P0 + (2/9)P1 + (4/9)P2 + (8/27)P3 (t=2/3)
Q3 = P3 (t=1)
分别将Q0、Q1、Q2、Q3的x、y坐标代入方程组求解,可得:
P0(120, 0)
P1(35, -27.5)
P2(-27.5, 35)
P3(0, 120)
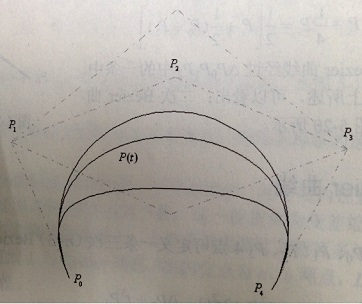
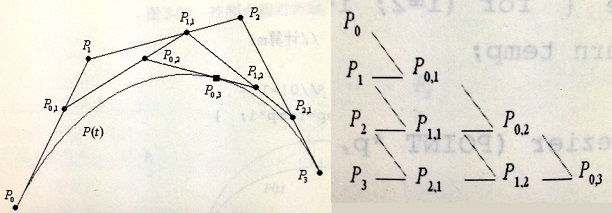
Bezier曲线的几何作图法
以控制点数为4,边数为3的控制多边形P0P1P2P3为例:
1)分别在边P0P1、P1P2 、P2P3上找到一点P0,1、P1,1 、P2,1,该点将所在的边分成 t:(1-t) 两部分,比如设 t =2/3。
2)然后,将3个分割点构成新的控制多边形P0,1P1,1P2,1,其控制点数为3,边数为2;再以同样的方法及同样的比例,对边P0,1P1,1和边P1,1P2,1进行分割,得到分割点P0,2和P1,2。
3)最后,对边P0,2P1,2进行相同比例的分割,得到点P0,3。P0,3即为由原控制多边形P0P1P2P3所确定的三次Bezier曲线上的参数为t 的点P(t)。
4)若让参数 t 在[0, 1]变动,并且让△t 取一个较小的增量,如△t =0.1。循环多次即可作出三次Bezier曲线。
Bezier曲线的几何作图法示意图以及分割点的递推关系
Bezier曲线的几何作图法总结:
对于任意控制多边形,在以PiPi+1为端点的第 i条边上,找一点Pi,1(t),把该边分成t:(1-t) 比例,则分割点Pi,1(t)=(1-t)Pi + tPi+1 (i=0,1,…,n-1),这n个点组成一个新的n-1边形,对该多边形重复上述操作,得到一个新的n-2边形的顶点Pi,2(t) (i=0,1,…,n-2),依次类推,连续作n次后,得到一个单点Pi,n(t),该点就是Bezier曲线上参数为t的点P(t),让t 在[0, 1]变动,就得到Bezier曲线。
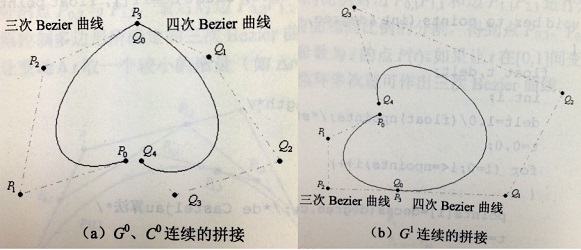
Bezier曲线的拼接
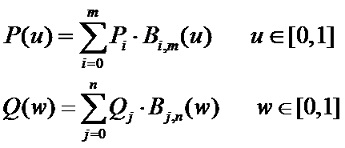
考虑两条Bezier曲线的一阶连续性(C1和G1)拼接设计:
1)由端点切矢量条件:
P’(1)=m(Pm-Pm-1) Q’(0)=n(Q1-Q0)
2)若曲线P(u)与Q(w)首尾拼接达到G1连续,必有Pm与Q0重合,并且Q’(0)=lP’(1) (l >0),即:
Q0=Pm Q1=Q0+(λm/n)*(Pm-Pm-1)
3)上式的几何意义:P(u)与Q(w)两条Bezier曲线拼接达到G1连续时,控制点Pm-1、Pm(=Q0)和Q1在一条直线上。
4)当λ=1时,P(u)与Q(w)两条Bezier曲线拼接可达到C1连续。
Bezier曲面
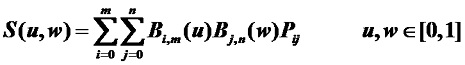
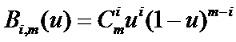 和
和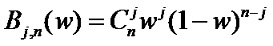 是Bernstein基函数。
是Bernstein基函数。
Bezier曲面的矩阵表示为:
1、双线性Bezier曲面
当m=n=1时,定义一张双线性Bezier曲面:
2、双二次Bezier曲面
当m=n=2时,定义一张双二次Bezier曲面,其边界曲线及参数坐标曲线均为抛物线:
3、双三次Bezier曲面
当m=n=3时,定义一张双三次Bezier曲面,它由16个顶点定义,参数曲线u、v都是三次Bezier曲线,该曲面只通过4个角点P00、P30、P03、P33:








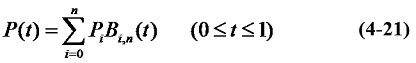
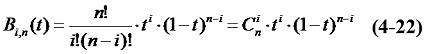

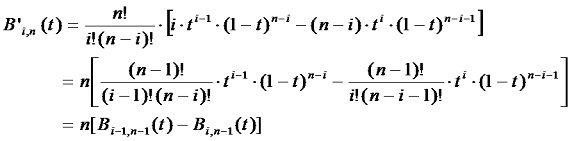
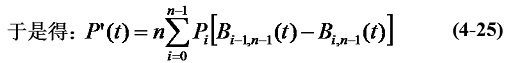
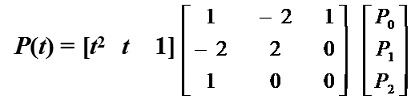
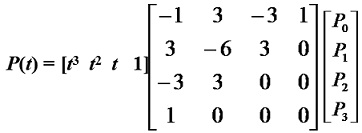
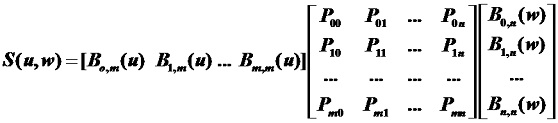
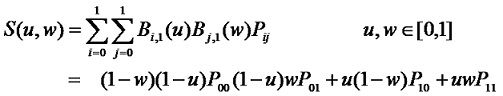
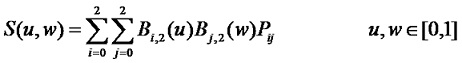
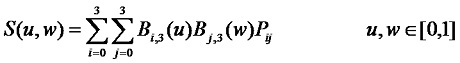














 3470
3470

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








