（六）数据结构面试必问

什么是链表、队列、栈？

链表：

    当需要存储多个相同数据类型的时候，可以使用数组存储，数组可以通过下标直接访问，但数组有个缺点就是无法动态的插入或删除其中的元素（特别是操作第一个位置上的元素），而链表弥补了这个缺陷，对于元素的插入和删除操作是很方便的，不过访问元素的“性能”就差很多了。

    所谓单链表，即只有一个指针，指向下一个元素（结点）的地址，只要知道单链表的首地址，就可以遍历整个链表了。由于链表结点是在堆区动态申请的，其地址并不是连续的，因此无法进行随机访问，只有通过前一结点的next指针才能定位到下一个结点的指针。

    单链表只能向后遍历，不能逆序遍历，所以有了使用更广泛的双链表。即结点多了一个存储前一个结点地址的prev指针。双链表可以双向遍历，但也只能按顺序访问。

 

队列：

    队列就像我们平时排队一样，按照数据到达的顺序进行排队，每次新插入的一个结点排在队尾，删除一个结点只能从头才能出队。简言之，对元素的到达顺序，按照“先进先出”的原则。由于队列频繁的插入和删除，一般为了高效，使用固定长度的数组实现，并且可循环使用数组空间，在操作之前要判断处理的队列是否已满或为空。如果要动态长度，可以用链表实现，只要同时记住链表的首地址（队头front）和尾地址（队尾rear）。

 

栈：

     栈的特点正好与队列相反，按照数据进栈的逆序出栈，即“先进后出”，每次入栈将元素放在栈顶，出栈时也只能从栈顶出栈，与队列类似，一般用定长数组存储栈元素，而不是动态的申请结点空间。进栈一般被叫做压栈，出栈被叫做弹栈。

    由于压栈弹栈都在栈顶，所以只需要一个size字段存储当前栈的大小，初始化size为0，每次压栈时，size+1，注意栈是否已满,弹栈则size-1。

 

什么是树（平衡二叉树、二叉排序树、B树、B+树、R树、红黑树）？

参考：https://blog.csdn.net/v_july_v/article/details/6530142

    为什么会有树这个概念呢？因为已有的数据结构（数组、链表）不能很好的平衡静态操作和动态操作的时间开销。

时间复杂度	数组	链表
静态操作（查找）	O(1)	O(n)
动态操作（插入、删除）	O(n)	O(1)

    对于树这种数据结构而言，最显著的特点就是有且只能有一个根节点（空树除外），每个节点可以有多个子结点，除了根结点，其他结点只能有一个父结点。树的种类繁多，一般谈论的最多的是二叉树，每个结点有不超过两个的子结点。

 

平衡二叉树 & 二叉排序树

    二叉排序树（Binary Search Tree，BST，也叫二叉搜索树），构造一棵二叉排序树也很简单，大于根节点的放在根节点的右子树上，小于根结点的放在根结点的左子树上（等于根结点的视情况而定）。如果写程序的话，可以采用递归的方式，而且由于不存在重叠子问题的情况，因此递归的性能已经足够好(不考虑栈溢出的情况)。

    二叉排序树在通常情况下可以达到O(lgn)的静态、动态操作的时间复杂度，但是存在一种特殊情况，若输入的本来就是有序的，这时二叉树就退化成了链表。为了消除二叉树对于输入的敏感特性，引入了平衡二叉树（AVL），事实上平衡二叉树应该叫平衡二叉排序树也合理。平衡二叉树只要保证每个节点左子树和右子树的高度差小于等于1就可以了。

 

B树 & B+树

    1981年，盖茨曾说“640kb对每个人来说是足够的”，现在看来像是一个笑话，可能当时intel生产的内存只有640KB，目前好一点的机器都已经达到16GB的内存了，但是事实上这句话仍然有一定的道理。

    操作系统中，我们应该学过寄存器的访问速度和容量是此消彼涨的，速度最快的当属CPU上火了寄存器，然后就是cache（高速缓存），然后是内存，再就是外部磁盘等，当两个处在不同层级的存储器（比如内存和外部磁盘）交换数据时，我们称之为I/O。而I/O相当耗时，要尽量避免使用。

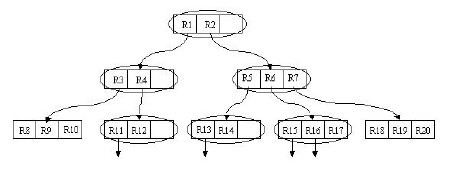
    B树（B-Tree，“B-树”这种翻译我不是很认同）的出现就是为了解决这个问题。B树由于是多路二叉树（根结点有两个子结点，其他结点子结点不止两个），它的高度要远低于平衡二叉树，一般来讲，二叉平衡树每下降一层就执行一次磁盘I/O操作，以1GB数据为例，平均需要30次磁盘I/O才能读取到数据，而B树每下降一层，每个结点都会读入多个关键码，因此B树适用于实现磁盘的读写逻辑。

      B 树是为了磁盘或其它存储设备而设计的一种多叉（相对于二叉树，B树每个内结点有多个分支，即多叉）平衡排序树。与下面要介绍的红黑树很相似，但在降低磁盘I/0操作方面要更好一些。许多数据库系统都一般使用B树或者B树的变形结构（如B+树）来存储信息。

 

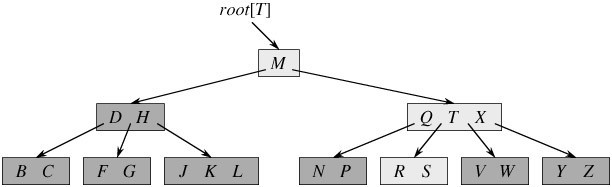
    从上图你能轻易的看到，一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女。如含有2个关键字D H的内结点有3个子女，而含有3个关键字Q T X的内结点有4个子女。

      B树中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小，根据磁盘驱动(disk drives)的不同，一般块的大小在1k~4k左右)；这样树的深度降低了，这就意味着查找一个元素只要很少结点从外存磁盘中读入内存，很快访问到要查找的数据。

 Bucket Li："mysql 底层存储是用B+树实现的，why？内存中B+树是没有优势的，但是一到磁盘，B+树的威力就出来了"。

 

B树：有序数组+平衡多叉树；   B+树：有序数组链表+平衡多叉树；   B*树：一棵丰满的B+树。

    

R树

    处理空间存储问题，R树在数据库等领域做出的功绩是非常显著的。它很好的解决了在高维空间搜索等问题。举个R树在现实领域中能够解决的例子：查找20英里以内所有的餐厅。如果没有R树你会怎么解决？一般情况下我们会把餐厅的坐标(x,y)分为两个字段存放在数据库中，一个字段记录经度，另一个字段记录纬度。这样的话我们就需要遍历所有的餐厅获取其位置信息，然后计算是否满足要求。如果一个地区有100家餐厅的话，我们就要进行100次位置计算操作了，如果应用到谷歌地图这种超大数据库中，这种方法便必定不可行了。

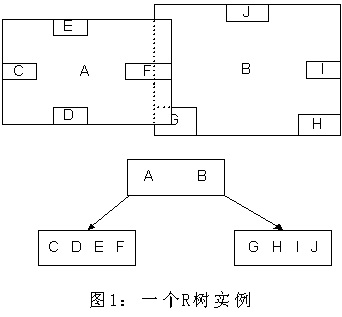
    R树就很好的解决了这种高维空间搜索问题。它把B树的思想很好的扩展到了多维空间，采用了B树分割空间的思想，并在添加、删除操作时采用合并、分解结点的方法，保证树的平衡性。因此，R树就是一棵用来存储高维数据的平衡树。

    每个R树的叶子结点包含了多个指向不同数据的指针，这些数据可以是存放在硬盘中的，也可以是存在内存中。根据R树的这种数据结构，当我们需要进行一个高维空间查询时，我们只需要遍历少数几个叶子结点所包含的指针，查看这些指针指向的数据是否满足要求即可。这种方式使我们不必遍历所有数据即可获得答案，效率显著提高。

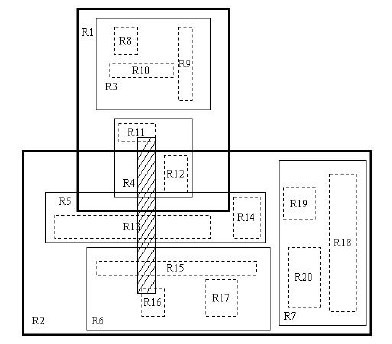
    R树是一种能够有效进行高维空间搜索的数据结构，它已经被广泛应用在各种数据库及其相关的应用中。但R树的处理也具有局限性，它的最佳应用范围是处理2至6维的数据，更高维的存储会变得非常复杂，这样就不适用了。近年来，R树也出现了很多变体，R*树就是其中的一种，这些变体提升了R树的性能。

 

红黑树

面试参看：https://www.cnblogs.com/wuchanming/p/4444961.html

     R-B Tree，全称是Red-Black Tree，又称为“红黑树”，它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

    红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。例如，Java集合中的TreeSet和TreeMap，C++ STL中的set、map，需要使用动态规则的防火墙系统，使用红黑树而不是散列表被实践证明具有更好的伸缩性。Linux内核在管理vm_area_struct（虚拟内存）时就是采用了红黑树来维护内存块的。

    对于链表、数组、树和图来说，它们每次的动态操作都会完全遗忘之前的状态，转而到达全新的状态，这种数据结构称为ephemeral structure。另一种数据结构可以记录某一历史时刻的状态，在访问时可以根据版本好+目标数据进行访问，这种数据结构称为persistent structure。事实上，红黑树可以实现这种对历史版本的记录。

    B树与红黑树最大的不同在于，B树的结点可以有许多子女，从几个到几千个。那为什么又说B树与红黑树很相似呢?因为与红黑树一样，一棵含n个结点的B树的高度也为O（lgn），但可能比一棵红黑树的高度小许多，应为它的分支因子比较大。所以，B树可以在O（logn）时间内，实现各种如插入（insert），删除（delete）等动态集合操作。

 

 

什么是堆（大根堆、小根堆）？

    这里说的“堆”是一种数据结构，注意与jvm中的堆内存分开。堆必须满足以下两个条件：（1）是完全二叉树  （2）heap中存储的值是偏序（偏序只对部分元素成立关系R,全序对集合中任意两个元素都有关系R）。

    大根堆：父结点的值大于等于其子结点的值；小根堆：父结点的值小于等于其子节点的值。

  

堆的存储：

    一般用数组来存储堆，第i个结点的父结点下标为,（i-1）/2，它的左右子结点的下标为i*2+1，i*2+2。

插入一个元素：

    新元素被加入到heap的末尾，然后更新树以恢复堆的次序。每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中。以大根堆为例：

删除一个元素：

    按定义，堆中每次都删除第0个数据。为了便于重建堆，实际的操作是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最大的，如果父结点比这个最小的子结点还大说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。

 

 

什么是图（有向图、无向图、拓扑）？

图：一种较线性表和树更为复杂的数据结构。图结构中结点之间的关系是任意的，图中任何两个节点都可能有关系。图通常用来描述某些事物之间的某种特定关系 ，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

线性表：数据元素之间仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继 
树：树形结构中，数据元素之间有着明显的层次关系，并且每一层上的数据元素可能和下一层中多个元素（即其孩子结点）相关，但只能和上一层中一个元素（即其双亲结点）相关

    在通常状况下，区分图的有向和无向的区别在于边的有向性。

有向图的基本算法： 拓扑排序（数据结构之拓扑排序）、联通分量、最短路径（Dijkstra算法和Floyd算法）。

无向图的基本算法：最小生成树（Prime算法。Kruska算法）、DFS、BFS、MFS、最短路径、最大连通图、强联通分量。

  

   

 

栈和队列的相同之处和不同之处？

相同点：①都是线性结构    ②插入操作都是在表尾进行   ③ 插入和删除的时间复杂度都是O(1)，在空间复杂度上也相同                              ④都可以通过顺序结构和链表实现    ⑤多链栈和多链队列的管理模式可以相同。

不同点：①删除数据元素的位置不同，栈在表尾进行，队列在表头进行    ②顺序栈能够实现多栈空间共享，而顺序队列不能。                  ③应用场景不同；常见栈的应用场景包括括号问题的求解，表达式的转换和求值，函数调用和递归实现，深度优先搜索遍历等；常见的队列的应用场景包括计算机系统中各种资源的管理，消息缓冲器的管理和广度优先搜索遍历等。   

 

栈通常采用的两种存储结构。

https://blog.csdn.net/sandmm112/article/details/79860236

 

两个栈实现队列，两个队列实现栈。

◆两个栈实现队列，实现队列的入队（enqueue）和出队（dequeue）操作。

    栈的特性是先进后出（FILO）,队列的特性是先进先出（FIFO）,在实现dequeue时，我们的难点是如何将栈中最底层的数据拿出来，我们有两个栈，所以我们可以将一个栈中的数据依次拿出来压入到另一个为空的栈，另一个栈中数据的顺序恰好是先压入栈1的元素此时在栈2的上面。

图（1）：将队列中的元素“abcd”压入stack1中，此时stack2为空；

图（2）：将stack1中的元素pop进stack2中，此时pop一下stack2中的元素，就可以达到和队列删除数据一样的顺序了；

图（3）：可能有些人很疑惑，就像图3，当stack2只pop了一个元素a时，satck1中可能还会插入元素e,这时如果将stack1中的元素e插入stack2中，在a之后出栈的元素就是e了，显然，这样想是不对的，我们必须规定当stack2中的元素pop完之后，也就是satck2为空时，再插入stack1中的元素。

 

用两个队列实现一个栈 

     因为队列是先进先出，所以要拿到队列中最后压入的数据，只能每次将队列中数据dequeue至最后一个，此时这个数据为最后enqueue入队列的数据，在每次dequeue时，将数据enqueue至队列2中。每次执行delete操作时，循环往复。（感觉效率低）每次删除时间复杂度O(N) 

图（1）：当栈里面插入元素“abcd”的时候，元素a在栈底（最后出去），d在栈顶（最先出去）；

图（2）：将元素“abc”从q1中头删，然后再q2中尾插进来之后，头删q1中的元素“d”，就相当于实现了栈顶元素的出栈；

图（3）：同理，将元素“ab”从q2中头删，然后尾插到q1中，然后再头删q2中的元素“c”;

图（4）：同理，删除元素“b”;

图（5）：当栈又插入一个元素“e”时，此时元素“a”不能从队列中删除，而是将元素“a”插入q2中，再删除q1中的元素“e”,最后再删除元素“a”。

说明：其中红色框代表该队列中的元素出队列，该队列为空。