【CFD理论】对流项-02

最新推荐文章于 2024-06-17 22:40:32 发布
最新推荐文章于 2024-06-17 22:40:32 发布
阅读量305 收藏
点赞数
分类专栏： of初阶 文章标签： 机器学习 线性代数 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/zq93538196/article/details/126297947
版权

【CFD理论】对流项-02

知识回顾

在这里插入图片描述
a E = D − F 2 a_E=D-\frac{F}{2} aE​=D−2F​
a W = D + F 2 a_W=D+\frac{F}{2} aW​=D+2F​

边界问题

Dirichlet
Newmann
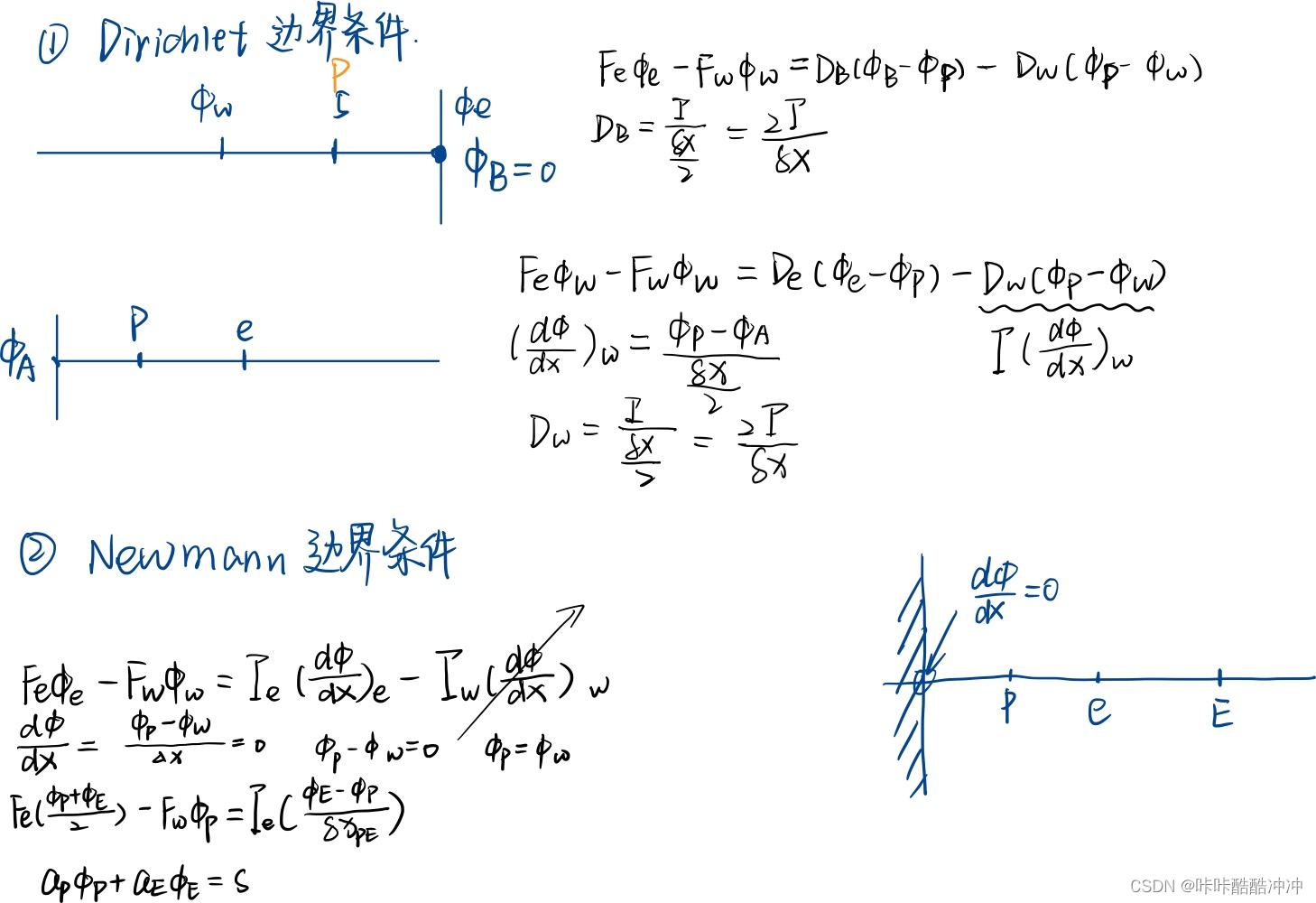
在这里插入图片描述

properties of discretisation schemes

conservation 守恒性

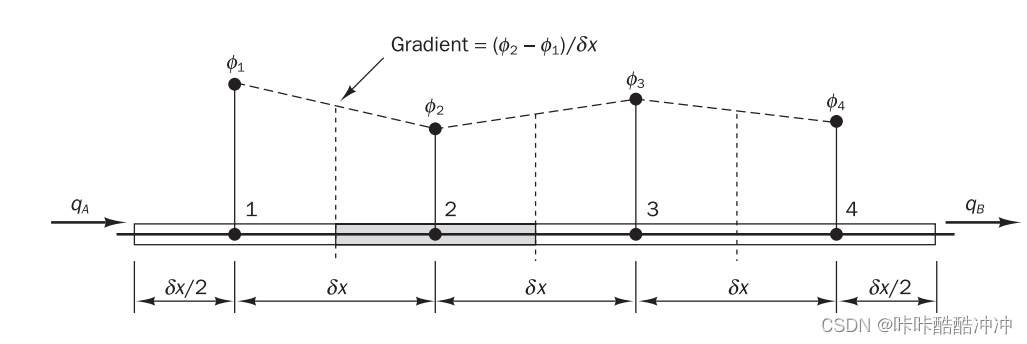
在这里插入图片描述
用纯扩散性方程分析：
( Γ ϕ 2 − ϕ 1 δ x − q A ) + ( Γ ϕ 3 − ϕ 2 δ x − Γ ϕ 2 − ϕ 1 δ x ) + ( Γ ϕ 4 − ϕ 3 δ x − Γ ϕ 3 − ϕ 2 δ x ) + ( q B − Γ ϕ 4 − ϕ 3 δ x ) = q B − q A (\Gamma\frac{\phi_2-\phi_1}{\delta x}-q_A)+(\Gamma\frac{\phi_3-\phi_2}{\delta x}-\Gamma\frac{\phi_2-\phi_1}{\delta x})+(\Gamma\frac{\phi_4-\phi_3}{\delta x}-\Gamma\frac{\phi_3-\phi_2}{\delta x})+(q_B-\Gamma\frac{\phi_4-\phi_3}{\delta x})=q_B-q_A (Γδxϕ2​−ϕ1​​−qA​)+(Γδxϕ3​−ϕ2​​−Γδxϕ2​−ϕ1​​)+(Γδxϕ4​−ϕ3​​−Γδxϕ3​−ϕ2​​)+(qB​−Γδxϕ4​−ϕ3​​)=qB​−qA​

Boundedness 有界性

  • 对角占优 diagonally dominant
  • ϕ \phi ϕ应该在neighboring nods的值范围内
  • 离散方程的所有系数应具有相同的符号
    不过不符合以上条件，就可能越界 产生“wiggles”现象
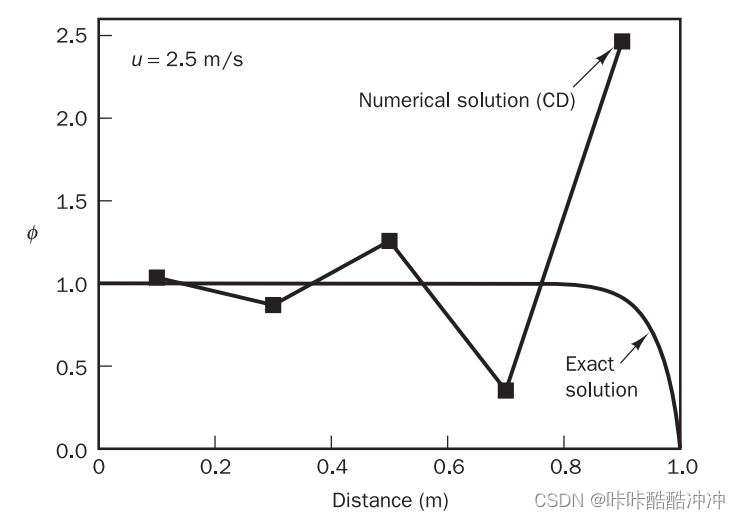
    在这里插入图片描述
example

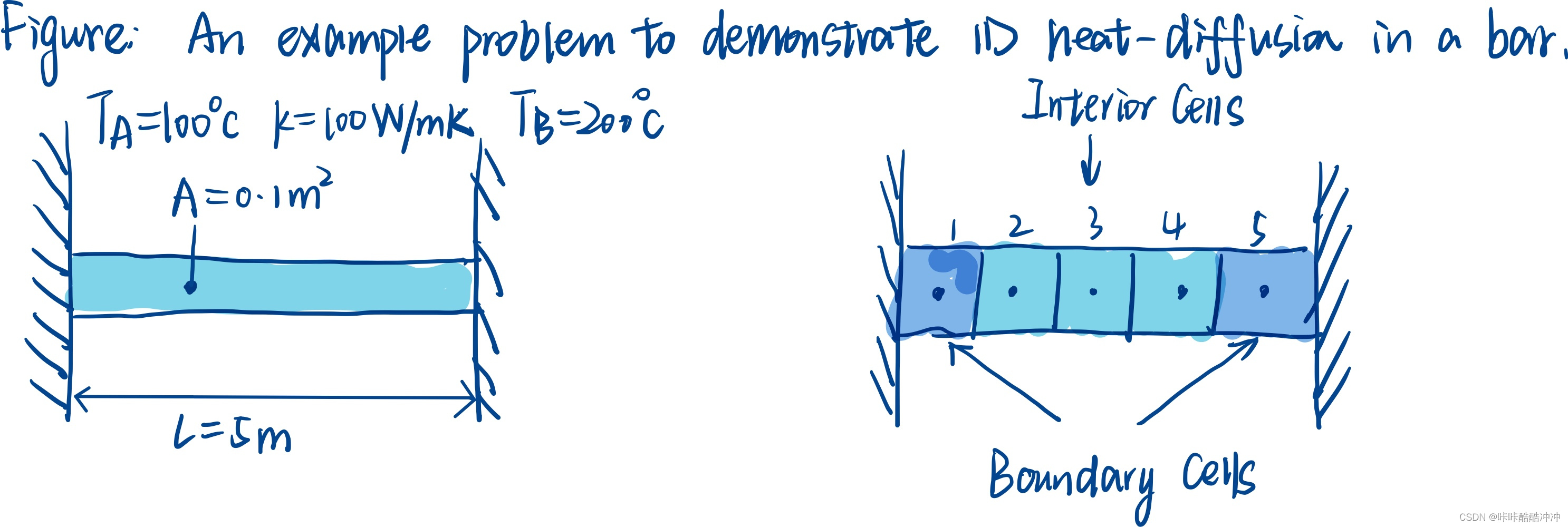
在这里插入图片描述
一维稳态扩散方程
d d x ( k d T d x ) + S = 0 \frac{d}{dx}(k\frac{dT}{dx})+S=0 dxd​(kdxdT​)+S=0
( k A T R − T P d P R ) − ( k A T P − T L d L P ) + S ‾ V = 0 (kA\frac{T_R-T_P}{d_{PR}})-(kA\frac{T_P-T_L}{d_{LP}})+\overline S V=0 (kAdPR​TR​−TP​​)−(kAdLP​TP​−TL​​)+SV=0

  • 内部网格：
    ( k A d T d x ) r − ( k A d T d x ) l + S ‾ V = 0 (kA\frac{dT}{dx})_r-(kA\frac{dT}{dx})_l+\overline S V=0 (kAdxdT​)r​−(kAdxdT​)l​+SV=0
    T P ( D l A l + D r A r + 0 ) = T L ( D l A l ) + T R ( D r A r ) + S ‾ V = 0 T_P(D_lA_l+D_rA_r+0)=T_L(D_lA_l)+T_R(D_rA_r)+\overline SV=0 TP​(Dl​Al​+Dr​Ar​+0)=TL​(Dl​Al​)+TR​(Dr​Ar​)+SV=0
  • 边界网格：
    ( k A d T d x ) r − ( k A d T d x ) l + S ‾ V = 0 (kA\frac{dT}{dx})_r-(kA\frac{dT}{dx})_l+\overline S V=0 (kAdxdT​)r​−(kAdxdT​)l​+SV=0
    left
    ( d T d x ) l = T P − T A d L P / 2 (\frac{dT}{dx})_l=\frac{T_P-T_A}{d_{LP/2}} (dxdT​)l​=dLP/2​TP​−TA​​
    ( k A T R − T P d P R ) − ( k l T P − T A d L P / 2 ) + V ‾ = 0 (kA\frac{T_R-T_P}{d_{PR}})-(kl\frac{T_P-T_A}{d_{LP}/2})+\overline V=0 (kAdPR​TR​−TP​​)−(kldLP​/2TP​−TA​​)+V=0
    T P ( 0 + D A + 2 D A ) = T L ( 0 ) + T R ( D A ) + T A ( 2 D A ) + S ‾ V T_P(0+DA+2DA)=T_L(0)+T_R(DA)+T_A(2DA)+\overline SV TP​(0+DA+2DA)=TL​(0)+TR​(DA)+TA​(2DA)+SV
    right
    T P ( D A + 0 + 2 D A ) = T L ( D l A l ) + T R ( 0 ) + T B ( 2 D A ) + S ‾ V T_P(DA+0+2DA)=T_L(D_lA_l)+T_R(0)+T_B(2DA)+\overline SV TP​(DA+0+2DA)=TL​(Dl​Al​)+TR​(0)+TB​(2DA)+SV
  1. 分割网格
    L c e l l = L N = 1 m L_cell=\frac{L}{N}=1m Lc​ell=NL​=1m
  2. 分配材料属性
    D A = 10 ∗ 0.1 / 1 = 10 [ W / K ] DA=10*0.1/1=10[W/K] DA=10∗0.1/1=10[W/K]
    S ‾ V = 1000 ∗ 0.1 ∗ 1 = 100 [ W ] \overline S V=1000*0.1*1=100[W] SV=1000∗0.1∗1=100[W]
  3. 矩阵系数
A matrix:
  30.0  -10.0    0.0    0.0    0.0 
 -10.0   20.0  -10.0    0.0    0.0 
   0.0  -10.0   20.0  -10.0    0.0 
   0.0    0.0  -10.0   20.0  -10.0 
   0.0    0.0    0.0  -10.0   30.0 
   
B vector:
2100.0
 100.0
 100.0
 100.0
4100.0
  1. 求解矩阵
    T = A / B T=A/B T=A/B
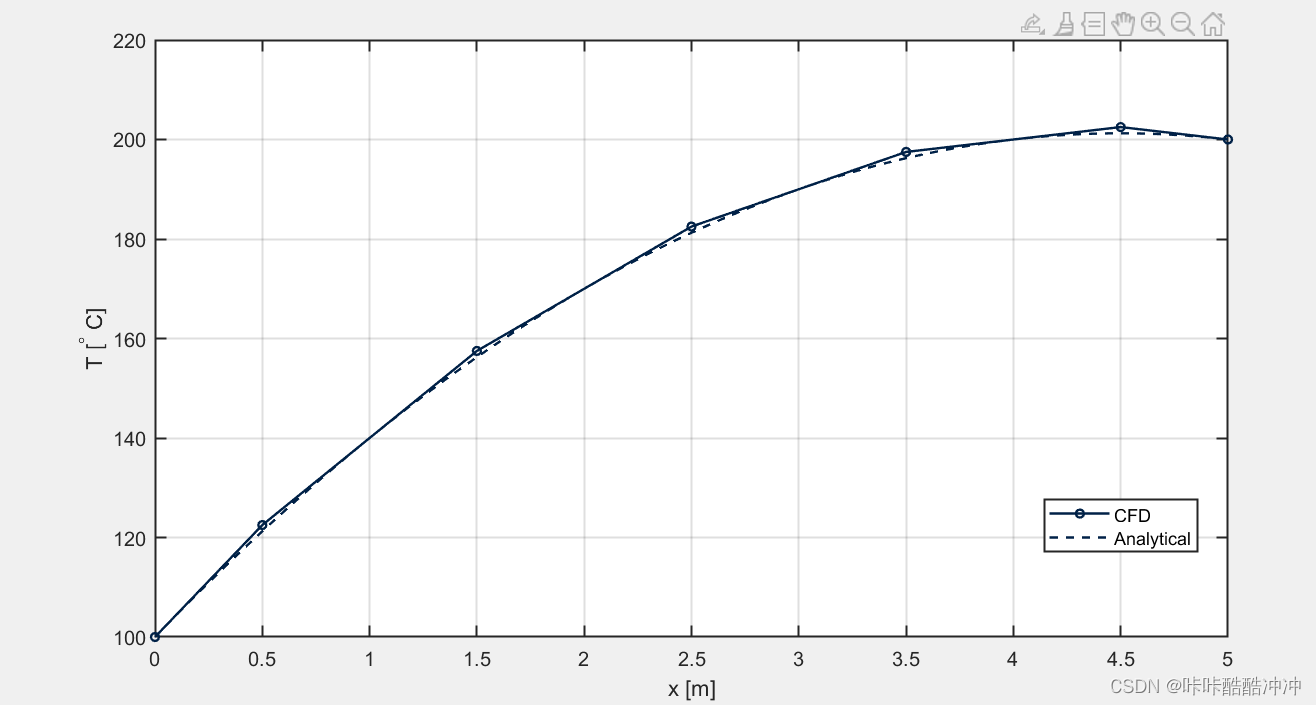
    在这里插入图片描述
case2- wiggle-对流扩散
close all; clear; clc
%--------------------------------------------------------------------------
% User Inputs
%--------------------------------------------------------------------------

% Thermal Conductivity of the fluid (W/mK)
cond = 0.1;

% Specific heat capacity of the bar (J/Kg K)
cp = 1;

% Cross-sectional Area of the channel (m2)
area = 1;

% Length of the channel (m)
barLength = 1;

% Number of cells in the mesh
nCells = 5;

% Temperature at the left hand side of the channel (deg C)
tempLeft = 1;

% Temperature at the right hand side of the channel (deg C)
tempRight = 0;

% Heat source per unit volume (W/m3)
heatSourcePerVol = 0;

% Flow velocity (m/s)
flowVelocity = 2.5;

% Fluid Density (kg/m3)
fluidDensity = 1.0;

% Plot the data? ('true' / 'false')
plotOutput = 'true';

% Print the set up data? (table of coefficients and matrices)
printSetup = 'true';

% Print the solution output (the temperature vector)
printSolution = 'true';

% =========================================================================
% Code Begins Here
% =========================================================================
%--------------------------------------------------------------------------
% 1. Print messages
%--------------------------------------------------------------------------
fprintf('================================================\n');
fprintf('\n');
fprintf('   solve1DConvectionDiffusionEquationUpwind.m\n')
fprintf('\n')
fprintf(' - Fluid Mechanics 101\n')
fprintf(' - Author: Dr. Aidan Wimshurst\n')
fprintf(' - Contact: FluidMechanics101@gmail.com\n')
fprintf('\n')
fprintf(' [Exercise 1: Chapter 4]\n')
fprintf('================================================\n')

%--------------------------------------------------------------------------
% 2. Create the mesh of cells
%--------------------------------------------------------------------------

fprintf(' Creating Mesh ...\n');
fprintf('------------------------------------------------\n');

% Start by calculating the coordinates of the cell faces
xFaces = linspace(0, barLength, nCells+1);

% Calculate the coordinates of the cell centroids
xCentroids = 0.5*(xFaces(2:end) + xFaces(1:end-1));

% Calculate the length of each cell
cellLength = xFaces(2:end) - xFaces(1:end-1);

% Calculate the distance between cell centroids
dCentroids = xCentroids(2:end) - xCentroids(1:end-1);

% For the boundary cell on the left, the distance is double the distance
% from the cell centroid to the boundary face
dLeft = 2*(xCentroids(1) - xFaces(1));

% For the boundary cell on the right, the distance is double the distance from
% the cell centroid to the boundary cell face
dRight = 2*(xFaces(end) - xCentroids(end));

% Append these to the vector of distances
dCentroids = [dLeft, dCentroids, dRight];

% Compute the cell volume
cellVolumes = cellLength*area;

%--------------------------------------------------------------------------
% 2.0 Calculate the Matrix Coefficients
%--------------------------------------------------------------------------

fprintf(' Calculating Matrix Coefficients\n');
fprintf('------------------------------------------------\n');

% Diffusive flux per unit area
DA = area*cond./dCentroids;

% Convective flux
velocityVector = flowVelocity*ones(1, nCells+1);
densityVector = fluidDensity*ones(1, nCells+1);
F = densityVector.*velocityVector*area*cp;

% Evaluate the Peclet Number
Pe = F./DA;

% Calculate the source term Sp
Sp = zeros(1, nCells);

% Assign sources to the left and right hand boundaries
Sp(1) = -1.0*(2.0*DA(1) +F(1));
Sp(end) = -1.0*(2.0*DA(end) -F(end));

% Calculate the source term Su
Su = heatSourcePerVol*cellVolumes;

% Assign sources to the left and right hand boundaries
Su(1) = 3.5*tempLeft;
Su(end) = -3.5*tempRight;

% Left Coefficient (aL)
aL = DA(1:end-1) + (F(1:end-1)/2);

%Right Coefficient (aR)
aR = DA(2:end) + (-F(2:end)/2);

% Set the first element of aL to zero. It is a boundary face
aL(1) = 0;

% Set the last element of aR to zero. It is a boundary face
aR(end) = 0;

% Create the central coefficients
aP = aL + aR  - Sp;

%--------------------------------------------------------------------------
% 3.0 Create the matrices
%--------------------------------------------------------------------------

fprintf(' Assembling Matrices\n');
fprintf('------------------------------------------------\n');

% Start by creating an empty A matrix and an empty B matrix
Amatrix = zeros(nCells, nCells);
BVector = zeros(nCells, 1);

% Populate the matrix one row at a time (i.e one cell at a time)
%
% NOTE: this method is deliberately inefficient for this problem
% but it is useful for learning purposes. We could populate the
% diagonals and the off-diagonals directly.

for i = 1:nCells

    % Do the A matrix Coefficients

    % Left boundary Cell
    if (i == 1)

        Amatrix(i, i) = aP(i);
        Amatrix(i, i+1) = -1.0*aR(i);

    % Right Boundary Cell
    elseif(i == nCells)

        Amatrix(i, i-1) = -1.0*aL(i);
        Amatrix(i, i) = aP(i);

    % Interior Cells
    else

        Amatrix(i, i-1) = -1.0*aL(i);
        Amatrix(i, i) = aP(i);
        Amatrix(i, i+1) = -1.0*aR(i);
    end
    
    % Do the B matrix coefficients
    BVector(i) = Su(i);
end

%--------------------------------------------------------------------------
% 4.0 Print the setup
%--------------------------------------------------------------------------

if strcmp(printSetup, 'true')
    fprintf(' Summary: Set Up\n')
    fprintf('------------------------------------------------\n')
    fprintf('aL: ')
    for i = 1:nCells
       fprintf('%6.1f ', aL(i)); 
    end
    fprintf('\n')
    fprintf('aR: ')
    for i = 1:nCells
       fprintf('%6.1f ', aR(i)); 
    end
    fprintf('\n')
    fprintf('aP: ')
    for i = 1:nCells
       fprintf('%6.1f ', aP(i)); 
    end
    fprintf('\n')
    fprintf('Sp: ')
    for i = 1:nCells
       fprintf('%6.1f ', Sp(i)); 
    end
    fprintf('\n')
    fprintf('Su: ')
    for i = 1:nCells
       fprintf('%6.1f ', Su(i)); 
    end
    fprintf('\n')
    fprintf('Pe: ')
    for i = 1:nCells+1
       fprintf('%6.1f ', Pe(i)); 
    end
    fprintf('\n')
    fprintf('A matrix:\n')
    for i = 1:nCells
        for j = 1:nCells
           fprintf('%6.1f ', Amatrix(i, j)); 
        end
        fprintf('\n')
    end
    fprintf('B vector:\n')
    for i = 1:nCells
       fprintf('%6.1f\n', BVector(i)); 
    end
    fprintf('\n')
    fprintf('------------------------------------------------\n')
end

%--------------------------------------------------------------------------
% 5.0 Solve the matrices
%--------------------------------------------------------------------------

fprintf(' Solving ...\n')
fprintf('------------------------------------------------\n')

% Use MATLAB's default linear algebra solver (AX = B)
Tvector = Amatrix \ BVector;

fprintf(' Equations Solved.\n')
fprintf('------------------------------------------------\n')

%--------------------------------------------------------------------------
% 6.0 Print the Solution
%--------------------------------------------------------------------------
if strcmp(printSolution, 'true')
    fprintf(' Solution: Temperature Vector\n');
    fprintf('------------------------------------------------\n');
    fprintf('T vector:\n')
    for i = 1:nCells
       fprintf('%10.6f\n', Tvector(i)); 
    end
    fprintf('\n')
    fprintf('------------------------------------------------\n')
end

%--------------------------------------------------------------------------
% 7.0 Plot the solution
%--------------------------------------------------------------------------

% Plot the data if desired
if strcmp(plotOutput,'true')

    fprintf(' Plotting ...\n')
    fprintf('------------------------------------------------\n')
    
    % Append the boundary temperature values to the vector, so we can
    % plot the complete solution
    xPlotting = [xFaces(1), xCentroids, xFaces(end)];
    temperaturePlotting = [tempLeft; Tvector; tempRight];

    % Figure Size Parameters
    figSizeXcm = 8.5;
    aspectRatio = 4.0/3.0;
    figSizeYcm = figSizeXcm / aspectRatio;
    figSizeXpixels = figSizeXcm * 37.79527559055118;
    figSizeYpixels = figSizeYcm * 37.79527559055118;

    % Figure font, text and line widths
    fontSize = 10;
    fontChoice = 'Arial';
    lineWidth = 1.0;
    markerSize = 4;
    
    % Colours for the line plots
    colour1 = 'black';
    colour2 = [0.0, 0.129, 0.2784];

    % Adjust anchor for where figure shows up on screen (px)
    x0 = 100;
    y0 = 100;

    fig1 = figure('Name', '1D Diffusion');
    box on;
    hold on;
    plot(xPlotting, temperaturePlotting, 'k-o', 'Color', colour2, ...
        'MarkerSize', markerSize, 'linewidth', lineWidth + 0.2);
    hold off;
    xlabel('x [m]', 'FontSize', fontSize)
    ylabel('T [^{\circ} C]', 'FontSize', fontSize)
    grid on;
    set(gca, 'fontsize', fontSize);
    set(gca, 'linewidth', lineWidth);
    set(gcf, 'position', [x0, y0, figSizeXpixels, figSizeYpixels]);
    legend({'CFD'}, 'NumColumns', 1, 'Location', 'Best')
    
end

%==========================================================================
% END OF FILE
%==========================================================================

结果：

================================================
 Creating Mesh ...
------------------------------------------------
 Calculating Matrix Coefficients
------------------------------------------------
 Assembling Matrices
------------------------------------------------
 Summary: Set Up
------------------------------------------------
aL:    0.0    1.8    1.8    1.8    1.8 
aR:   -0.8   -0.7   -0.7   -0.8    0.0 
aP:    2.8    1.0    1.0    1.0    0.3 
Sp:   -3.5    0.0    0.0    0.0    1.5 
Su:    3.5    0.0    0.0    0.0   -0.0 
Pe:    5.0    5.0    5.0    5.0    5.0    5.0 
A matrix:
   2.8    0.8    0.0    0.0    0.0 
  -1.8    1.0    0.7    0.0    0.0 
   0.0   -1.8    1.0    0.7    0.0 
   0.0    0.0   -1.8    1.0    0.8 
   0.0    0.0    0.0   -1.8    0.3 
B vector:
   3.5
   0.0
   0.0
   0.0
  -0.0

------------------------------------------------
 Solving ...
------------------------------------------------
 Equations Solved.
------------------------------------------------
 Solution: Temperature Vector
------------------------------------------------
T vector:
  1.035630
  0.869355
  1.257331
  0.352053
  2.464370

------------------------------------------------
 Plotting ...
------------------------------------------------

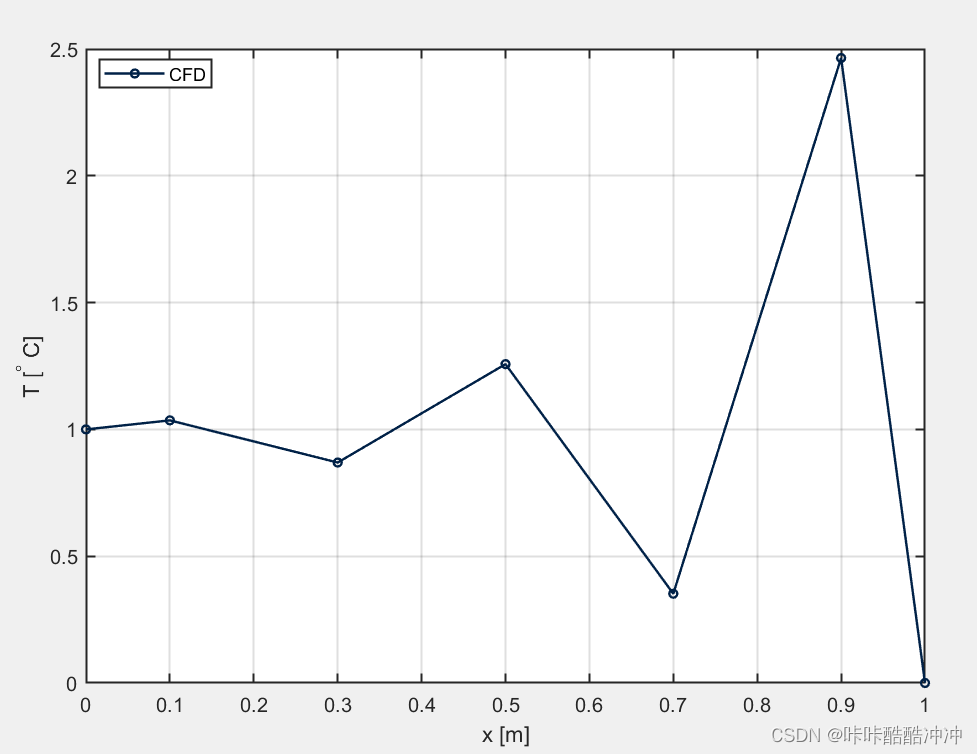
在这里插入图片描述

  • CD方法计算，Pe数大（5）造成越界

参考：

  • book-An Introduction to Computational Fluid Dynamics, The Finite Volume Method
================================================

   solve1DConvectionDiffusionEquationUpwind.m

 - Fluid Mechanics 101
 - Author: Dr. Aidan Wimshurst
 - Contact: FluidMechanics101@gmail.com

 [Exercise 1: Chapter 4]

Transportiveness 输运性

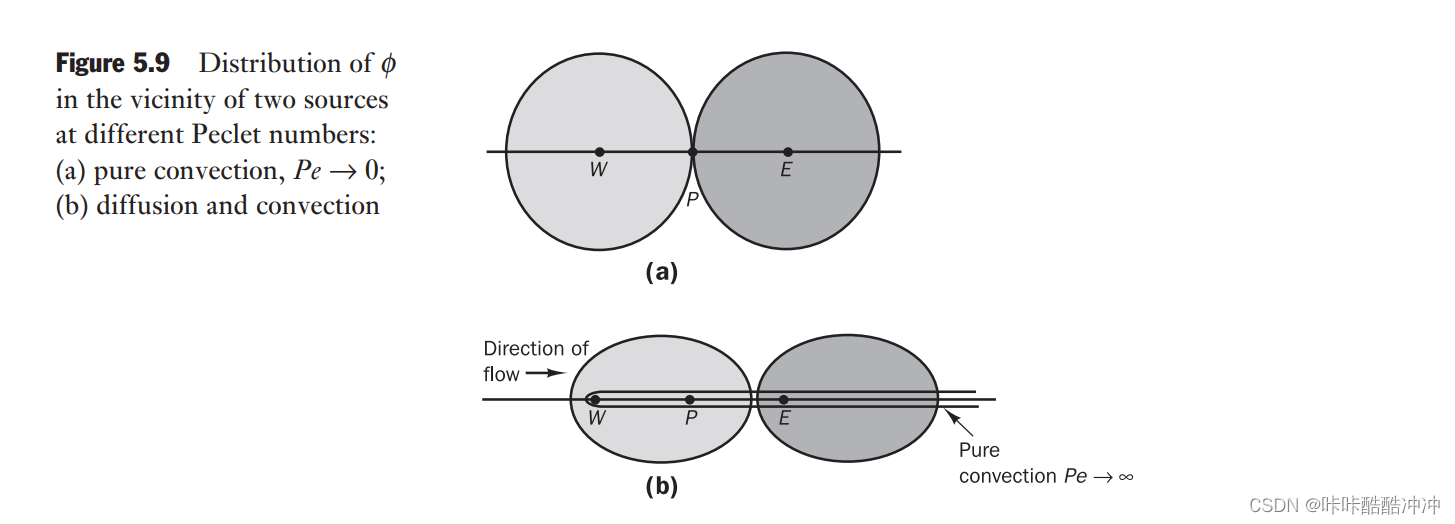
在这里插入图片描述

Accuracy 精度

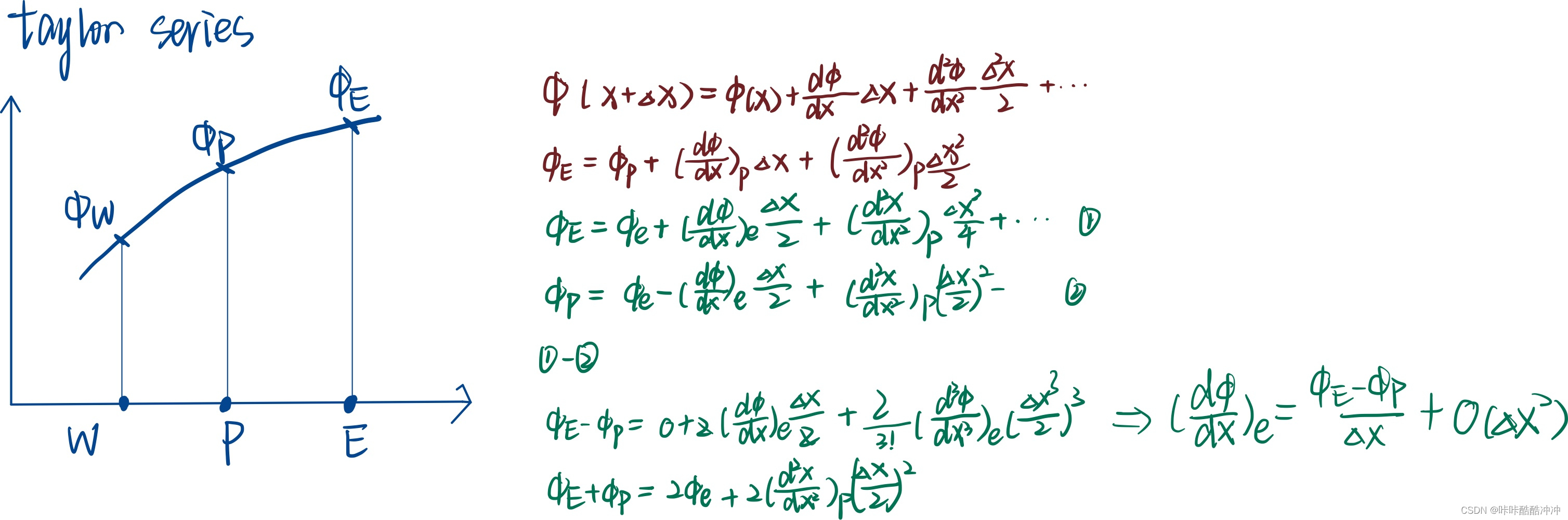
在这里插入图片描述

QUICK格式3阶

ϕ e = 3 8 ϕ E + 6 8 ϕ P − 1 8 ϕ W \phi_e=\frac{3}{8}\phi_E+\frac{6}{8}\phi_P- \frac{1}{8} \phi_W ϕe​=83​ϕE​+86​ϕP​−81​ϕW​

  • 用了三个点，三阶格式
  1. 迎风格式，非常稳定的格式，不会越界，守恒，一阶格式，会带来smear现象。
  2. CD，可能会导致越界，二阶
  3. 二阶迎风格式
  4. QUICK，三阶格式
咔咔酷酷冲冲
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
Navier-Stokes方程的对流项系数对湍流性质的影响
12-28
Navier-Stokes方程的对流项系数对湍流性质的影响，杨玉尧，，为了研究Kolmogorov常数以及耗散常数等常数的普适性和本质的物理意义，基于对对流项系数进行修正后的Navier-Stokes方程，对各向同向性均�
ANSYS CFD-Post Tutorials.pdf
07-25
ANSYS CFD-Post官方例子讲义，详细讲解了ANSYS CFD后处理的操作步骤和方法，是学习CFD-Post的必备资料。
【CFD理论】对流项-01
zq93538196的博客
08-12 989
对流项介绍
【CFD理论】对流项-03
zq93538196的博客
08-17 584
QUICK,TVD
【CFD理论】对流项-04-TVD
zq93538196的博客
08-18 966
TVD
【CFD理论】对流项-06高分格式
zq93538196的博客
08-27 495
TVD,NVD.非结构化网格计算案例 NVF ϕ~=ϕ−ϕUϕD−ϕUϕ~f=f(ϕU,ϕC,ϕD) \tilde{\phi}=\frac{\phi-\phi_U}{\phi_D-\phi_U}\\ \tilde\phi_f=f(\phi_U,\phi_C,\phi_D)\\ ϕ~​=ϕD​−ϕU​ϕ−ϕU​​ϕ~​f​=f(ϕU​,ϕC​,ϕD​) TVD
【CFD理论】对流项-05-非结构化网格
zq93538196的博客
08-19 343
非结构化网格TVD
【CFD理论】扩散项-01
zq93538196的博客
07-31 842
扩散项的公式推导和练习题
3.2.1 对流项离散格式的基本介绍 | 3.2.2 中心离散格式与一阶迎风格式（OpenFOAM理论笔记系列）
CloudBird07的博客
08-28 5027
3.2 对流项的离散格式 3.2.1 对流项离散格式的基本介绍 在开始本节的讨论开始，笔者首先要说明，本节所介绍的内容相对于整个对流项离散格式的开发的历史可以说是极其简略的。可以这么说，整个计算流体动力学发展的历史有一半以上是由对流项离散格式写成的。本节的内容以Versteeg和Malalasekera的著作《An Introduction to Computational Fluid Dynamic: The Finite Volume Method Second edition》中的对流项离散格式介绍内
第十三周：CFD基础理论+Fluent实例学习
2301_79714145的博客
12-03 758
本周主要尝试了热传导和对流方面的Fluent案例学习，明白了其常用模型的理论基础和实际运用间的差别，几乎无需进行多处修改，在fluent的默认参数中即可进行收敛计算。但在网格划分的部分中，网格质量小于案例中的质量，现在原因还未找出，但版本不同的概率较大。在CFD理论中，对有限差分法的理论和数学物理基础进行了更深入的学习，受益匪浅。
CFD-FASTRAN简介.rar
05-07
CFD-FASTRAN简介.rar
ANSYS CFD-Post Users Guide.pdf
11-05
ANSYS CFD-Post用户指南简介 ANSYS CFD-Post是一款功能强大且功能齐全的计算流体动力学（CFD）后处理软件，由ANSYS公司开发。该软件旨在帮助用户快速、可靠地分析和可视化复杂的流体动力学仿真结果，提高科学研究和...
Couple CFD-DEM Modeling.pdf
03-19
Couple CFD-DEM Modeling
CFD-POST导出数据方法.pdf
08-25
从CFD-Post导出数据的方法，包括导出一个点的数据和导出点云的数据，因为有时候在模拟的过程中，需要一个平面的速度、压力、温度分布情况，可以在平面上按照某个规律取n个点，得到各点的数值。
线性代数|机器学习-P15矩阵A的低秩变换下的逆矩阵
scar2016的博客
06-17 516
假设我们有一个单位矩阵I，列向量u,v那么当我们对单位向量I减去秩为1的矩阵后，其逆等于多少？
【Python】深入了解聚类：从原理到实践
2333333
06-17 524
聚类是一种将数据点分组的技术，其目标是最大化组内数据点的相似性，最小化组间数据点的相似性。与监督学习不同，聚类不依赖于已标记的数据，而是根据数据本身的特征进行分组。
【机器学习】基于顺序到顺序Transformer机器翻译
MUKAMO的博客
06-17 899
本文深入探讨了序列到序列(Seq2Seq)模型和Transformer架构在机器翻译任务中的应用。通过编码器和解码器的工作流程，Seq2Seq模型有效处理了不同长度的序列转换问题。Transformer模型以其自注意力机制和并行处理能力，在处理长距离依赖时表现卓越。文中还介绍了模型的实现细节、数据预处理、向量化、模型训练和序列解码的完整流程。
AI存储解决案例分享
最新发布
存储随笔
06-17 509
阿里云利用对象存储 OSS 的能力，构建统一的数据湖存储，利用对象存储 OSS 的海量扩展、低成本的存储能力，搭建 AI 场景数据存储底座。AI应用程序在处理大规模数据集和复杂模型训练时，往往展现出独特的IO模型，特别是当提到"数百万个小IO读写操作"时，AI工作负载，尤其是在深度学习训练阶段，经常涉及对大量小块数据的频繁读取和写入操作。分层存储：采用多层次存储方案，将频繁访问的数据或活跃数据缓存在高速存储（如SSD）中，而较少访问的数据则存储在低成本但容量大的存储（如HDD）中。
cfd中扩散方程与扩散-对流方程的区别
03-21
扩散方程描述的是物质在无流动情况下的扩散过程，而扩散-...在扩散-对流方程中，除了扩散项外，还有对流项，它描述了物质随着流体的运动而移动的过程。因此，扩散-对流方程比扩散方程更加全面地描述了物质的传输过程。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值