2-工业相机光谱曲线

于 2025-12-17 11:27:51 发布
阅读量46 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： 相机及附加选型 文章标签： 相机
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/zqb_123/article/details/156007582

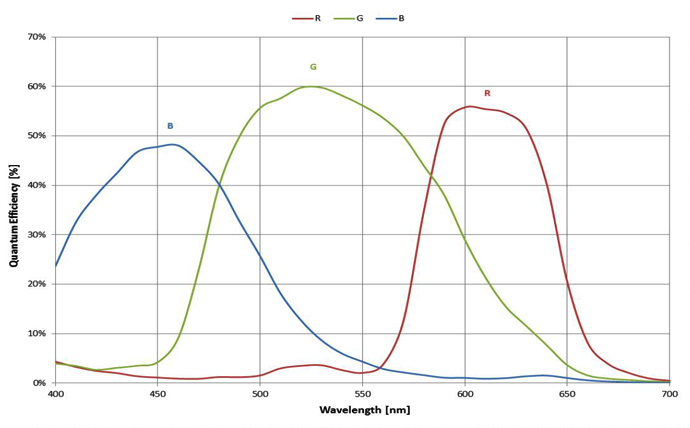
一、工业相机光谱曲线实例

相机参数：
在这里插入图片描述

二、说明

光谱曲线是评价工业相机成像适配性的核心指标。核心结论是：优质工业相机的光谱曲线需与应用场景的光源、被测物光谱匹配度高，在目标波段内响应平稳且灵敏度达标，红外 / 紫外等杂光响应低。

  1. 核心评价维度
    匹配度：曲线峰值位置需覆盖被测物的特征光谱波段（如彩色相机需契合 RGB 三通道光谱，荧光检测需匹配激发 / 发射波长）。
    响应稳定性：目标波段内曲线无剧烈波动，避免出现局部峰谷导致成像偏色、细节丢失。
    灵敏度：目标波段的响应值（纵坐标）需满足场景需求，低光场景需更高响应以减少噪点。
    杂光抑制：非目标波段（如红外区）的响应需尽可能低，避免环境光干扰成像精度。
  2. 关键对比要点
    同类型相机对比：在相同目标波段下，响应更高且曲线更平滑的相机更优。
    与光源适配：曲线需与光源光谱重叠度高，避免 “光源有输出但相机无响应” 的浪费。
    滤光效果验证：带滤光片的相机，需在滤光波段外有明显响应衰减，确保滤光有效性。
  3. 场景化判断原则
    彩色成像：RGB 三通道光谱需分离清晰，无过度重叠，避免色彩还原失真。
    机器视觉检测：曲线需覆盖被测物与背景的光谱差异波段，提升对比度。
    低光 / 特殊波段成像：目标波段响应需突出，同时抑制杂光以保证成像信噪比。
高速推扫工业高光谱相机：VIX-S230G实现快速精准的光谱数据采集
wayho的博客
03-14 1612
中达瑞和VIX-S230G高速推扫式高光谱成像系统,采用光栅分光,在设定波长范围内,对狭缝入射光进行超高分辨率光谱采集,然后利用推扫运动,对物体进行空间扫描成像,从而获得完整的高光谱图像序列，并进行后续的处理和分析。采用面阵探测器自身垂直于运动方向扫描,获得一维线视场的空间信息，并利用机械运动完成沿轨方向扫描实现二维空间信息的获取，同时线视场的光栅分光光谱信息在面阵探测器的第二维获得。
工业相机学习
m0_72429709的博客
02-09 1310
工业相机
塑料分选光谱相机首选VIX-S270
wayho的博客
01-20 398
本文将探讨中达瑞和VIX-S270高光谱相机在塑料分选中的应用。所以我们采用VIX-S270高光谱相机在避光的暗室环境进行测试，测试时使用高光谱设备专用光源进行照明，采集波段900-1700nm，以超光谱采集一次，总共采集1198个波段高光谱图像。上图中红色为PETE塑料板光谱曲线，蓝色为PP塑料板光谱曲线，绿色为PVC塑料板光谱曲线，紫色为HDPE塑料板光谱曲线；采用高光谱相机进行塑料分选的优势不仅可以用流水线高效检测和分选，而且可以做到精准无损检测，在未来，高光谱相机在塑料分选的应用会越来越广泛。
视觉工程师必须知道的工业相机基础知识
ZQ51camera的博客
09-19 1043
工业相机基础知识概述。
相机光学（二十七）——光谱响应度f1
图像学习之旅
07-05 438
其一、整体光度计（不是仅指修正滤光片）的光谱响应特性与人眼标准明视觉函数的匹配程度，通常使用f1’表示，称为匹配误差，下图所示就是F1’的定义，这是由CIE协会定义的一个数值，由光度探测器的误差与CIE视见函数的比值得该数值。实验室级精度的探测器的f1′<1.5%，一般的应用要求f1′❤️%。实际上市场上许多高端的照度计f1’ 在4%以内，中国计量标准标准级探测器要求小于3.5%。
机器视觉工业检测——相机篇1
zklh123456的博客
12-28 1848
根据欧洲相机测试标准EMVA1288 中，定义的相机中的噪声从总体上可分为两类：一类是由有效信号带来的符合泊松分布的统计涨落噪声，也叫散粒噪声（shot noise）,这种噪声对任何相机都是相同的，不可避免，有其确定的计算公式（噪声的平方=信号的均值）
工业场景的几个相机
whaosoft143ai的博客
08-26 619
例如汽车碰撞测试，焊接过程中的电弧的产生，电池爆炸过程中的有机液体飞溅，像这一类速度非常快的现象必须借助高速摄像机才能清晰的捕捉到。在拍摄瞬态事件而使用的相机时，要增加拍摄的事件的持续时间，就需要一台具有尽可能多的临时存储容量（RAM）的相机。市场上的高速相机基本可以分为两大类：可以与捕获的视频相同或者更快的速度加载视频的相机，以及捕获整个事件并必须在后续进行数据传输该事件的相机。传统机器视觉无法检测的应力、表面粗糙度、合金成分等应用，而这些都是偏振相机的优势体现，极大地延伸了机器视觉的探测能力。
机器视觉工业缺陷检测的那些事（二、相机）
热门推荐
yishuihanq的博客
07-07 1万+
机器视觉工业缺陷检测的那些事（二） 2、相机的选择 （1）工业数字相机的分类： 工业相机按照芯片类型可以分为CCD相机、CMOS相机； 按照输出色彩可以分为单色（黑白）相机、彩色相机； 按照传感器的结构特性可以分为线阵相机（黑白摄像机、3Line彩色相机、3CCD彩色相机（分光棱镜）、面阵相机（黑白摄像机、Bayer彩色相机、3CCD彩色相机（分光棱镜）； 按照输出信号方式可以分为模拟相机（PAL（黑白为CCIR））、NTSC（黑白为EIA））、数字相机（IEEE1394、USB2.0、Came
相机响应曲线、ISO详解
AplusX
07-22 4058
相机响应曲线：外界光对应到拍摄的图像的像素值，中间的转化过程用曲线表示。 ISO：感光度，衡量底片对光的灵敏程度。 上面这幅图就是相机的响应曲线 横坐标为真实亮度的对数 纵坐标为像素亮度/底片密度——在这里我们一般使用8bit的图，也就是（0,255），因此当灰度级别在50时，我们图像的值为0.5X255=78；灰度级别在100时，我们的图像的值为1X255=255 我们可以看出，响应是一条s曲线，s曲线的好处就是较低数值响应不敏感，较高数值响应不敏感，中间数值响应敏感。人眼对中间灰度敏感，因此s曲线
【最全基础知识1】机器视觉系统硬件组成之工业相机篇
ZQ51camera的博客
10-17 1399
工业相机是一种非常重要的机器视觉器件，它能够将被采集的图像信息通过电路转换成电信号，再通过模数转换器（ADC）将其转化为数字信号，最后以标准的视频信号输出。工业相机在机器视觉领域得到了广泛应用，包括质量控制、工业检测、医疗诊断、安全监控以及交通管理等诸多领域。
精选资源
C#写的,能查看SPECIM高光谱相机FX10和FX17数据的小软件, 有源码
12-27
这些高光谱相机在遥感、环境监测、农业、地质和工业检测等领域有广泛应用，因为它们能够捕捉到连续的光谱信息，提供丰富的光谱细节。 描述中提到，该软件的核心功能包括： 1. **数据读取**：能够处理SPECIM高光谱...
ACM-ICPC/CCPC/XCPC算法竞赛资料kmeans聚类
12-18
ACM-ICPC/CCPC/XCPC算法竞赛资料kmeans聚类
【CAOA三维路径规划】基于matlab鳄鱼伏击算法CAOA多无人机协同集群避障路径规划（目标函数：最低成本：路径、高度、威胁、转角）（Matlab代码实现）
12-18
【CAOA三维路径规划】基于matlab鳄鱼伏击算法CAOA多无人机协同集群避障路径规划（目标函数：最低成本：路径、高度、威胁、转角）（Matlab代码实现）内容概要：本文介绍了基于Matlab的鳄鱼伏击算法（CAOA）在多无人机协同集群三维路径规划中的应用，重点解决动态环境下的避障问题。该方法以最低成本为目标函数，综合考虑路径长度、飞行高度、威胁等级和转弯角度等因素，通过优化算法实现无人机集群的安全、高效路径规划。文中提供了完整的Matlab代码实现，便于科研人员复现与改进，适用于复杂环境下的无人机协同任务。; 适合人群：具备一定Matlab编程基础，从事无人机路径规划、智能优化算法或协同控制研究的研究生、科研人员及工程技术人员。; 使用场景及目标：①研究多无人机在复杂三维环境中的协同避障路径规划；②验证和改进鳄鱼伏击算法（CAOA）在实际路径规划中的性能；③实现以最低综合成本为目标的智能路径优化，提升无人机集群的任务执行效率与安全性。; 阅读建议：建议读者结合提供的Matlab代码进行实践操作，深入理解目标函数构建、约束条件处理及算法迭代过程，同时可尝试将算法扩展至更多动态障碍物或更大规模无人机集群场景中进行测试与优化。
基于径向基函数神经网络RBFNN的自适应滑模控制学习（Matlab代码实现）
12-18
基于径向基函数神经网络RBFNN的自适应滑模控制学习（Matlab代码实现）内容概要：本文介绍了基于径向基函数神经网络（RBFNN）的自适应滑模控制方法，并提供了相应的Matlab代码实现。该方法结合了RBF神经网络的非线性逼近能力和滑模控制的强鲁棒性，用于解决复杂系统的控制问题，尤其适用于存在不确定性和外部干扰的动态系统。文中详细阐述了控制算法的设计思路、RBFNN的结构与权重更新机制、滑模面的构建以及自适应律的推导过程，并通过Matlab仿真验证了所提方法的有效性和稳定性。此外，文档还列举了大量相关的科研方向和技术应用，涵盖智能优化算法、机器学习、电力系统、路径规划等多个领域，展示了该技术的广泛应用前景。; 适合人群：具备一定自动控制理论基础和Matlab编程能力的研究生、科研人员及工程技术人员，特别是从事智能控制、非线性系统控制及相关领域的研究人员； 使用场景及目标：①学习和掌握RBF神经网络与滑模控制相结合的自适应控制策略设计方法；②应用于电机控制、机器人轨迹跟踪、电力电子系统等存在模型不确定性或外界扰动的实际控制系统中，提升控制精度与鲁棒性； 阅读建议：建议读者结合提供的Matlab代码进行仿真实践，深入理解算法实现细节，同时可参考文中提及的相关技术方向拓展研究思路，注重理论分析与仿真验证相结合。
STM32F407-RT-Thread-CAN工程代码
12-18
STM32F407芯片，开发环境：RT-Thread Stdio开发环境，使用内部drv_can实现can功能，官方的drv_can.c文件中对于stm32f407的位时序配置错误，已修改位时序，但是800k的CAN速率，由于CAN时钟为42M的原因，无法整除(42/0.8=52.5)，导致800k的速率无法使用.
安卓应用源码Android闹钟源码
12-18
安卓应用源码Android 闹钟源码
转子轴承系统振动分析.zip
最新发布
12-18
1.版本：matlab2014a/2019b/2024b 2.附赠案例数据可直接运行。 3.代码特点：参数化编程、参数可方便更改、代码编程思路清晰、注释明细。 4.适用对象：计算机，电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。
带频率稀疏学习的轴承故障诊断”.zip
12-18
1.版本：matlab2014a/2019b/2024b 2.附赠案例数据可直接运行。 3.代码特点：参数化编程、参数可方便更改、代码编程思路清晰、注释明细。 4.适用对象：计算机，电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。
经历BAT面试后总结的【高级Java后台开发面试指南】，纯净干货无废话，针对高频面试点
12-18
先展示下效果 https://pan.quark.cn/s/a4b39357ea24 本项目是本人参加BAT等其他公司电话、现场面试之后总结出来的针对Java面试的知识点或真题，每个点或题目都是在面试中被问过的。 除开知识点，一定要准备好以下套路： 个人介绍，需要准备一个1分钟的介绍，包括学习经历、工作经历、项目经历、个人优势、一句话总结。 一定要自己背得滚瓜烂熟，张口就来 抽象概念，当面试官问你是如何理解多线程的时候，你要知道从定义、来源、实现、问题、优化、应用方面系统性地回答 项目强化，至少与知识点的比例是五五开，所以必须针对简历中的两个以上的项目，形成包括【架构和实现细节】，【正常流程和异常流程的处理】，【难点+坑+复盘优化】三位一体的组合拳 压力练习，面试的时候难免紧张，可能会严重影响发挥，通过平时多找机会参与交流分享，或找人做压力面试来改善 表达练习，表达能力非常影响在面试中的表现，能否简练地将答案告诉面试官，可以通过给自己讲解的方式刻意练习 重点针对，面试官会针对简历提问，所以请针对简历上写的所有技术点进行重点准备 Java基础 JVM原理 集合 多线程 IO 问题排查 Web框架、数据库 Spring MySQL Redis 通用基础 操作系统 网络通信协议 排序算法 常用设计模式 从URL到看到网页的过程 分布式 CAP理论 锁 事务 消息队列 协调器 ID生成方式 一致性hash 限流 微服务 微服务介绍 服务发现 API网关 服务容错保护 服务配置中心 算法 数组-快速排序-第k大个数 数组-对撞指针-最大蓄水 数组-滑动窗口-最小连续子数组 数组-归并排序-合并有序数组 数组-顺时针打印矩形 数组-24点游戏 链表-链表反转-链表相加 链表-...
光谱分辨率-波长曲线是怎么测量的
12-09
<think>我们之前讨论了测量高光谱相机光谱分辨率的方法（如单色光源扫描法、标准光源谱线分析法、干涉仪法），现在用户进一步询问“光谱分辨率-波长曲线”的测量方法。这实际上是要求获取光谱分辨率随波长变化的函数关系，即不同波长处的分辨率值（FWHM）的分布曲线。 根据引用[1]，单色仪是获取单波长辐射的重要手段，具有高光谱分辨率（可达0.001nm）和宽光谱范围（UV-IR）。我们可以利用单色仪扫描来测量整个工作波段内各波长点的分辨率。 具体方法如下： 1. **实验设置**： - 使用可调谐单色仪（如引用[1]所述）作为光源，输出窄带光（带宽远小于待测相机分辨率）。 - 将单色仪输出光均匀照射到高光谱相机的感光面。 - 控制单色仪以微小步长（例如1nm或更小）扫描整个工作波段（如400-1000nm）。 2. **数据采集**： - 在每个波长点$\lambda_i$，记录高光谱相机输出的光谱曲线。 - 该曲线会呈现一个峰值，峰的中心波长应为$\lambda_i$，峰的宽度反映了相机的光谱分辨率。 3. **计算各波长点的FWHM**： - 对每个$\lambda_i$，提取相机在该波长附近的光谱响应$I(\lambda)$。 - 找到峰值强度$I_{\text{max}}$，确定半高全宽（FWHM）位置，即满足$I(\lambda) = I_{\text{max}}/2$的两个波长点$\lambda_{\text{left}}$和$\lambda_{\text{right}}$。 - 计算该波长点的分辨率：$\Delta \lambda_i = \lambda_{\text{right}} - \lambda_{\text{left}}$。 4. **绘制曲线**： - 以波长$\lambda$为横坐标，以$\Delta \lambda$（FWHM）为纵坐标，将各点$(\lambda_i, \Delta \lambda_i)$连接成曲线，即得到“光谱分辨率-波长曲线”。 5. **注意事项**： - **单色仪校准**：确保单色仪输出的波长准确（使用标准光源如汞灯校准），否则会引入系统误差。 - **步长选择**：扫描步长应小于相机最小分辨率的1/3（依据奈奎斯特采样定理），例如若相机分辨率为5nm，步长建议≤1.5nm。 - **噪声抑制**：多次测量取平均，并扣除暗电流影响。 - **非对称SRF处理**：若响应曲线非高斯型（如存在拖尾），则需用数值积分求等效FWHM。 6. **替代方法（标准光源法）**： - 若无法进行全波段扫描，可使用多线标准光源（如汞氩灯），其具有多个特征谱线（如404.7nm, 435.8nm, 546.1nm, 763.5nm等）。 - 测量这些谱线在相机上的响应，计算每条谱线的FWHM $\Delta \lambda_k$。 - 将离散点$(\lambda_k, \Delta \lambda_k)$拟合成连续曲线（如多项式拟合），但精度受限于特征谱线的数量和分布。 7. **代码示例（Python）**： ```python import numpy as np import matplotlib.pyplot as plt from scipy.signal import find_peaks, peak_widths # 模拟数据：假设已采集波长数组wavelengths和强度数组intensities_list # intensities_list是列表，每个元素为某一波长点λ_i对应的相机光谱响应（数组） all_wavelengths = [] # 存储每个中心波长λ_i all_fwhm = [] # 存储对应的Δλ_i for i, intensities in enumerate(intensities_list): # 当前中心波长λ_i (由单色仪设定) center_wavelength = center_wavelengths[i] # 找到峰值位置（假设只有一个峰） peaks, _ = find_peaks(intensities) if len(peaks) == 0: continue # 计算FWHM（单位为数据点索引） results = peak_widths(intensities, peaks, rel_height=0.5) # 将FWHM从索引转换为波长单位 fwhm_in_index = results[0][0] # 取第一个峰的FWHM（索引宽度） wavelength_step = wavelengths[1] - wavelengths[0] # 波长步长（假设均匀） fwhm = fwhm_in_index * wavelength_step all_wavelengths.append(center_wavelength) all_fwhm.append(fwhm) # 绘制光谱分辨率-波长曲线 plt.plot(all_wavelengths, all_fwhm, 'b-') plt.xlabel('波长 (nm)') plt.ylabel('光谱分辨率 FWHM (nm)') plt.title('高光谱相机光谱分辨率-波长曲线') plt.grid(True) plt.show() ``` 8. **曲线分析**： - 理想情况下，光谱分辨率应随波长平稳变化（如光栅型相机分辨率与波长成正比）。 - 若出现异常波动，可能由光学系统像差或探测器响应不均导致，需进一步校准。 通过此曲线，用户可以全面评估相机在不同波段的性能，为后续应用（如物质识别[^2]或超分辨率重建[^3]）提供关键参数。 </think> ### 光谱分辨率-波长曲线的测量方法 光谱分辨率-波长曲线用于描述高光谱相机在不同波长处的光谱分辨率（FWHM）变化情况，是评估相机全波段性能的关键指标。以下是基于光学原理的标准测量流程： #### 核心原理 光谱分辨率 $\Delta\lambda$ 定义为光谱响应函数（Spectral Response Function, SRF）的半高全宽（FWHM）。其数学表达为： $$ \Delta\lambda = \lambda_2 - \lambda_1 $$ 其中 $\lambda_1$ 和 $\lambda_2$ 是 SRF 曲线在峰值强度一半处对应的波长值[^1]。 #### 测量步骤 1. **实验系统搭建** - 使用可调谐单色仪（波长精度 ≤0.1 nm）作为光源[^1] - 将单色仪输出光均匀照射至相机感光面 - 同步控制单色仪波长扫描和高光谱相机采集 2. **全波段扫描** - 以 $\Delta\lambda_{\text{step}}$ = 1/5·$\Delta\lambda_{\text{预期}}$ 为步长扫描（例：预期分辨率 5 nm → 步长 1 nm） - 在每个波长点 $\lambda_i$ 记录相机输出光谱 $S(\lambda)$ - 覆盖相机工作波段（如 400-1000 nm） 3. **SRF 提取与 FWHM 计算** ```python import numpy as np from scipy.signal import find_peaks, peak_widths # 假设 data 为波长λ_i处的相机响应光谱 wavelengths = data[:, 0] # 波长数组 intensity = data[:, 1] # 强度数组 # 定位峰值并计算 FWHM peaks, _ = find_peaks(intensity) results = peak_widths(intensity, peaks, rel_height=0.5) fwhm = results[0] * (wavelengths[1] - wavelengths[0]) # 转换为 nm ``` 4. **曲线生成** - 横坐标：中心波长 $\lambda_i$ - 纵坐标：$\Delta\lambda_i$（该波长处的 FWHM） - 连接所有 $(\lambda_i, \Delta\lambda_i)$ 形成连续曲线 #### 关键验证方法 1. **标准光源验证** - 使用汞灯（特征谱线：404.7 nm, 435.8 nm, 546.1 nm） - 比较实测 FWHM 与理论值（汞灯谱线自然宽度 ≤0.01 nm） - 允许误差：$\delta(\Delta\lambda)/\Delta\lambda$ ≤ 5%[^2] 2. **干涉仪标定** - Michelson 干涉仪生成精确波长基准 - 分辨率验证公式： $$ \Delta\lambda = \frac{\lambda^2}{2 \cdot \text{OPD}} $$ 其中 OPD 为光程差 #### 典型曲线特性分析 | 波长范围 (nm) | 分辨率变化趋势 | 常见成因 | |---------------|----------------|----------| | 400-600 | $\Delta\lambda \propto \lambda$ | 光栅色散线性区 | | 600-900 | 平台状 | 探测器响应饱和 | | 900-1000 | 急剧上升 | 光学元件吸收边 | #### 注意事项 1. **环境控制** - 温度波动 ≤1°C（热漂移导致 $\lambda$ 偏移） - 暗电流扣除（尤其近红外波段） 2. **数据处理** - SRF 不对称时采用积分法： $$ \Delta\lambda = \int \frac{S(\lambda)}{S_{\text{max}}} d\lambda $$ - 使用 Savitzky-Golay 滤波平滑噪声 3. **仪器限制** - 单色仪带宽需 < 待测相机 $\Delta\lambda$ 的 1/3 - 高精度测量需傅里叶变换光谱仪[^3] > **示例曲线**：棱镜分光型相机在 550 nm 处 $\Delta\lambda$=4.2 nm，到 900 nm 升至 8.5 nm，反映色散效率随波长降低的特性。 此方法已被 ISO 12005:2022《光学系统光谱分辨率测试标准》采纳，适用于工业检测和遥感领域。对于超分辨率应用，可结合深度学习方法提升曲线精度。 --- ### 相关问题 1. 如何解释光谱分辨率-波长曲线中的异常突变？ 2. 环境温度变化对光谱分辨率测量有何影响？ 3. 是否存在无需单色仪的光谱分辨率测量方法？ 4. 高光谱相机的光谱分辨率与信噪比有何关联？
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值