贝叶斯，朴素贝叶斯的基础原理及例子

频率派和贝叶斯派

频率派认为，样本所属的分布参数$\theta$虽然是未知的，但是是固定的，可以通过样本对$\theta$进行预估得到$\theta \hat{}$。
贝叶斯派认为参数$\theta$是一个随机变量，不是一个固定的值，在样本产生前，会基于经验或者其他方法对$\theta$预先设定一个分布$\pi (\theta )$,称之为先验分布。之后会根据样本对$\theta$进行调整，修正，记为$\pi (\theta |x1,x2,x3,\dots \dots )$,称为后验分布。

贝叶斯公式的推导

为什么需要朴素贝叶斯

假设训练数据的属性由n维随机向量x表示，分类结果用随机变量y表示，那x和y的统计规律就可以用联合概率分布$P(X,Y)$描述，每个具体的样本$(x_i,y_i)$都可以通过$P(X,Y)$独立同分布的产生
贝叶斯分类器的出发点就是联合概率分布，根据条件概率性质可以得到
$P(X,Y)=P(Y)\ast P(X|Y)=P(X)\ast P(Y|X)$
其中
$P(Y)$：每个类别出现的概率，这是先验概率。
$P(X|Y)$：给定的类别下不同属性出现的概率，似然概率
先验概率很容易计算出来，只需要统计不同类别样本的数目即可，而似然概率受属性数目的影响，估计较为困难。
例如，每个样本包含100个属性，每个属性的取值可能有100种，那分类的每个结果，要计算的条件概率是1002=10000，数量量非常庞大。因此，这时候引进了朴素贝叶斯。

朴素贝叶斯是什么

朴素贝叶斯，加了个朴素，意思是更简单的贝叶斯。
朴素贝叶斯假定样本的不同属性满足条件独立性假设，并在此基础上应用贝叶斯定理执行分类任务。
对于给定的待分类项x，分析样本出现在每个类别中的后验概率，将后验概率最大的类作为x所属的类别
要解决似然概率难以估计的问题，就需要引入条件独立性假设
条件独立性假设保证了所有属性相互独立，互不影响，每个属性独立的对分类结果发生作用。
这样条件概率变成了属性条件概率的乘积
$P(X=x|Y=c)=P(X(1)=x(1),X(2)=x(2),\dots \dots ,X(n)=x(n)|Y=c)=\prod _{i=0}^{n}P(X^j=x^j|Y=c)$
这就是朴素贝叶斯方法，有了训练集，我们可以很轻易的算出先验概率$P(Y)$和似然概率$P(Y|X)$,这样我们就可以求得后验概率$P(X|Y)$

例子–西瓜书151页

首先我们有西瓜的数据集3.0。

我们面临一个问题。下列测试集是好瓜还是坏瓜？

我们首先可以算得先验概率

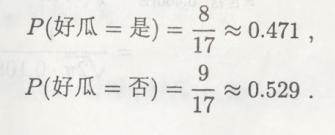
然后算出条件概率

然后计算好瓜和坏瓜的概率

0.063明显更大，所以大可能是好瓜。