leetcode_刷题总结(c++)_动态规划_背包类问题

已于 2022-07-07 16:31:59 修改
阅读量573 收藏
点赞数 1
分类专栏： leetcode 文章标签： leetcode 算法 数据结构
于 2022-05-15 19:01:15 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/zxm_jimin/article/details/124717014
版权

主要参考博客：

一篇文章吃透背包问题！（细致引入+解题模板+例题分析+代码呈现）
动态规划之背包问题以及优化为一维数组和完全背包问题（最易理解的讲解）
动态规划：关于01背包问题，你该了解这些！（滚动数组）

文章目录

背包定义

给定一个背包容量target，再给定一个数组nums(物品)，能否按一定方式选取nums中的元素得到target
注意：
1、背包容量target和物品nums的类型可能是数，也可能是字符串
2、target可能题目已经给出(显式)，也可能是需要从题目的信息中挖掘出来(非显式)(常见的非显式target比如sum/2等)
3、选取方式有常见的一下几种：每个元素选一次/每个元素选多次/选元素进行排列组合

背包分类

常见的背包类型主要有以下几种：
1、0/1背包问题：每个元素最多选取一次
2、完全背包问题：每个元素可以重复选择
3、组合背包问题：背包中的物品要考虑顺序
4、分组背包问题：不止一个背包，需要遍历每个背包

问题分类

1、最值问题：要求最大值/最小值
2、存在问题：是否存在…………，满足…………
3、组合问题：求所有满足……的排列组合

因此把背包类型和问题类型结合起来就会出现以下细分的题目类型：
1、0/1背包最值问题
2、0/1背包存在问题
3、0/1背包组合问题
4、完全背包最值问题
5、完全背包存在问题
6、完全背包组合问题
7、分组背包最值问题
8、分组背包存在问题
9、分组背包组合问题
这九类问题我认为几乎可以涵盖力扣上所有的背包问题

背包问题解题模板

二维dp模板

// 0-1背包问题模板代码(二维)
void bags(){
    vector<int> weight = {1, 3, 4};   //各个物品的重量
    vector<int> value = {15, 20, 30}; //对应的价值
    int bagWeight = 4;                //背包最大能放下多少重的物品

    // 二维数组：状态定义:dp[i][j]表示从0-i个物品中选择不超过j重量的物品的最大价值
    vector<vector<int>> dp(weight.size() + 1, vector<int>(bagWeight + 1, 0));

    // 初始化:第一列都是0，第一行表示只选取0号物品最大价值
    for(int j=bagWeight; j>=weight[0]; j--)
        dp[0][j]=dp[0][j-weight[0]]+value[0];

    // weight数组的大小 就是物品个数
    for(int i = 1; i <= weight.size(); i++){ // 遍历物品
		int num=weight[i-1])；
        for (int j=1; j <= bagWeight; j++){ // 遍历背包容量
            if(j < num])           //背包容量已经不足以拿第i个物品了
                dp[i][j] = dp[i-1][j]; //最大价值就是拿第i-1个物品的最大价值
            //背包容量足够拿第i个物品,可拿可不拿：
            //拿了最大价值是前i-1个物品扣除第i个物品的 重量的最大价值加上i个物品的价值
            //不拿就是前i-1个物品的最大价值,两者进行比较取较大的
            else
                dp[i][j]=max(dp[i-1][j], dp[ i-1][j-num]+value[i-1]);
        }
    }
    cout<<dp[weight.size()-1][bagWeight]<<endl;
}

滚动dp推导

二维代码可以进行优化，去除选取物品的那一层，简化为一维背包

在使用二维数组的时候，
递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把 dp[i - 1]那一层拷贝到dp[i] 上，
表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i-1]这一层拷贝到dp[i]上，不如只用一个一维数组dp[j]（一维数组，也可以理解是一个滚动数组）。
这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

遍历背包的顺序是不一样的：
二维dp遍历的时候，背包容量是从小到大；一维dp遍历的时候，背包是从大到小。

二维：
因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖。

一维：
如果正序遍历，那么物品0就会被重复加入多次，倒序遍历是为了保证物品i只被放入一次。
所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。

举例推导dp数组
输入：nums: [1, 1, 1, 1, 1], target = 4

一维dp，分别用物品0，物品1，物品2 来遍历背包，最终得到结果如下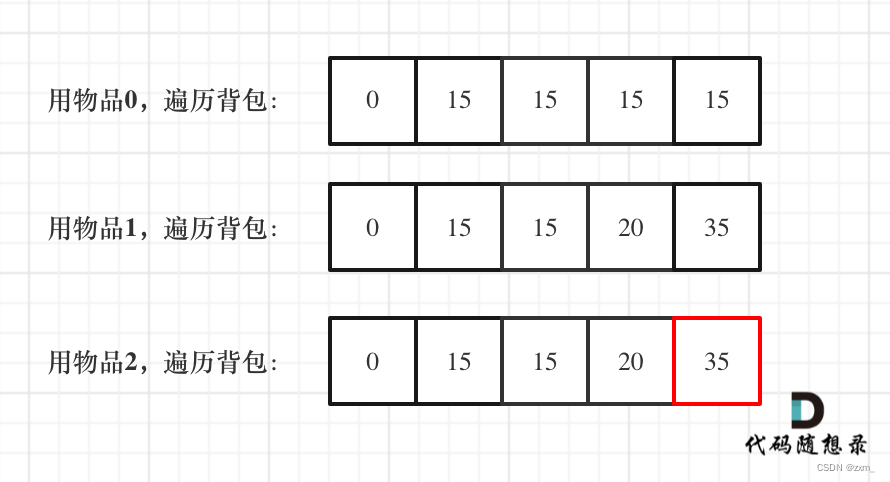：在这里插入图片描述

滚动dp模板


void bags(){
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    // 初始化
    // 一维 dp    状态定义：dp[j]表示容量为j的背包能放下东西的最大价值
    vector<int> dp(bagWeight + 1, 0);
    for (int i = 1; i < weight.size(); i++){ // 遍历物品
    	int num=weight[i-1];
        for (int j = bagWeight; j >=num; j--){// 遍历背包容量(一定要逆序)
            dp[j] = max(dp[j], dp[j - num] + value[i-1]); //不取或者取第i个（从0开始）
        }
    }
    cout << dp[bagWeight] << endl;
}

解题思路

1、两层循环
分别遍历物品nums和背包容量target

2、转移方程
根据背包的分类：确定物品和容量遍历的先后顺序
根据问题的分类：确定状态转移方程的写法

背包分类的模板（一维dp）

（注意：这里背包是从下标为0开始遍历）
1、0/1背包：
外循环nums,
内循环target,
target倒序且target>=nums[i];

（01背包用的是上一轮的结果，所以要倒序）
//dp[j] 全部初始化为0
dp[j] = max（dp[j]，dp[j- weight[i]] + value[i]）
此时的dp[j]其实是跟 上一个i-1的时候的dp[j] 去比较 （上一个的dp[j]是不能取到第i件物品的）。
如果能取到第i个物品(第i件物品能不能放下)，那么就比较不取第i件物品(dp[j])跟取到第i件物品的价值(dp[j- weight[i]] + value[i])。更新之后的dp[j]取较大值

dp[j]是能取第i件以及之前所有物品的最大价值，每次的比较都是围绕能取第i件（含之前的物品）以及第i-1件（含之前的物品）的价值。

2、完全背包：
外循环nums,
内循环target,
target正序且target>=nums[i];

完全背包中相反，采用顺序。前i件物品的dp[j-weight]+value，前i-1件物品的dp[j-weight]，前i-1件物品的dp[j]这三者的比较。也就是当前状态，需要先推导出重量j之前的当前状态，才能得到最大值。

3、组合背包：
外循环target,
内循环nums,
target正序且target>=nums[i];

4、分组背包：
这个比较特殊，需要三重循环：
外循环背包bags,
内部两层循环根据题目的要求转化为1,2,3三种背包类型的模板

问题分类的模板（一维dp）

看下标是从0开始 num=nums[j]
还是从1开始 num=nums[j-1]

1、最值问题:
dp[j] = max/min(dp[j], dp[j-num]+1) 或
dp[j] = max/min(dp[j], dp[j-num]+num);

2、存在问题(bool)：
dp[j]=dp[j] || dp[j-num];

3、组合问题：
dp[j]=dp[j]+dp[j-num];

01背包最值问题

最后一块石头的重量 II

1049. 最后一块石头的重量 II
在这里插入图片描述
思路：
最重要的是怎么转化为01背包问题

1、问题转化为：把一堆石头分成两堆,求两堆石头重量差最小值
进一步分析：
要让差值小,两堆石头的重量都要接近sum/2;
我们假设两堆分别为A,B,
A<sum/2,
B>sum/2,
若A更接近sum/2,B也相应更接近sum/2
2、进一步转化：将一堆stone放进最大容量为sum/2的背包,求放进去的石头的最大重量MaxWeight,
3、最终答案即为sum-2*MaxWeight;

二维dp
dp[i][j]:
从前i块石头中选取，选取值之和小于等于目标值j的最大值为dp[i][j]。（i、j分别对应从外到内两层循环。）

class Solution {
public:
    int lastStoneWeightII2(vector<int> &stones){
        int n=stones.size();
        int sum=accumulate(stones.begin(), stones.end(), 0);
        int target=sum/2;    
        vector<vector<int>> dp(n+1,vector<int>(target+1,0));
        for (int i=1; i<=n; i++){
            int cur=stones[i-1];
            for (int j=1; j<=target; j++){
                if(j<cur){
                    dp[i][j]=dp[i-1][j];
                }
                else{//j>=x
                    dp[i][j]=fmax(dp[i-1][j], dp[i-1][j-cur]+cur);
                }
                    
            }
        }
        return sum-dp[n][target]-dp[n][target];
    }
};

一维dp
dp[[j]:
表示容量为j的背包能放下东西的最大价值为dp[j]

class Solution {
public:
    int lastStoneWeightII(vector<int> &stones){
        int n=stones.size();
        int sum=accumulate(stones.begin(), stones.end(), 0);
        int target=sum/2;    
        vector<int> dp(target+1);
        for (int i=1; i<=n; i++){
            int cur=stones[i-1];
            for (int j=target; j>=cur; j--){
                    if(j<cur)
                        dp[j]=dp[j];
                    else
                        dp[j]=fmax(dp[j], dp[j-cur]+cur);
            }
        }
        return sum-dp[target]-dp[target];

    }
};

01背包存在性问题

分割等和子集

416. 分割等和子集

在这里插入图片描述

二维dp：
dp[i][j]:
对nums的前i个元素进行选取，dp[i][j]记录是否存在选取值相加结果为目标值j。
（dp是bool型）（i、j分别对应从外到内两层循环。）

class Solution {
public:
    bool canPartition2(vector<int>& nums) {
        int n=nums.size();
        if(n<2) {
            return false;
        }
        int sum = accumulate(nums.begin(), nums.end(), 0);
        int maxNum = *max_element(nums.begin(), nums.end());
        if(sum & 1) {
            return false;
        }
        int target=sum /2;
        if (maxNum>target) {
            return false;
        }
        vector<vector<int>> dp(n+1, vector<int>(target + 1, 0));
        for (int i=0; i<=n; i++)
            dp[i][0]=1;
        for(int j=1; j<=target; j++)
            dp[0][j]=0;
        dp[0][0]=1;
        for (int i=1; i<=n; i++) {
            int num=nums[i-1];
            for (int j=1; j<=target; j++){
                if (j<num){
                    dp[i][j]=dp[i - 1][j];
                } 
                else{
                    dp[i][j]=dp[i-1][j] | dp[i-1][j-num];
                }
            }
        }
        return dp[n][target];
    }
};

一维dp：
dp[j]:
dp[j]记录是否存在选取值相加结果为目标值j。

class Solution {
public:
    bool canPartition(vector<int> &nums){
        int n=nums.size();
        int sum = accumulate(nums.begin(), nums.end(), 0);
        if (sum % 2 == 1)  //如果是和为奇数显然无法分成两个等和子集
            return false;
        int target = sum / 2; 
        vector<int> dp(target + 1, 0); //dp[i]:是否存在子集和为i
        dp[0] = true;   //初始化：target=0不需要选择任何元素，所以是可以实现的
        for (int i=1; i<=n; i++){
            int cur=nums[i-1];
            for (int j=target; j>=cur; j--){
                dp[j]=dp[j] || dp[j-cur];
            }
        }
        return dp[target];
    }
};

01背包组合问题

目标和

494. 目标和
在这里插入图片描述
思路：
热评
在这里插入图片描述
sum( P ) 转化为01背包问题
用价值和重量都为nums数组的物品，较好凑满x=(target + sum)/2的背包方案数

二维数组：
dp[i][j]：
为前 i 位置中选取，能凑满值为目标值 j 的方案数为dp[i][j]

class Solution {
public:
    //dp
    int findTargetSumWays(vector<int>& nums, int target) {
        int n=nums.size();
        int sum=accumulate(nums.begin(), nums.end(), 0);
        if(sum<target || (sum+target)%2==1){
            return 0;
        }
        //转化为01背包后的目标值
        target=(target + sum)/2;
        if(target<0)
            return 0;
        vector<vector<int>> dp(n+1,vector<int>(target+1,0));
        //边界
        for(int i=0;i<=n;i++)
            dp[i][0] = 0;
        for(int j=1;j<=target;j++)
            dp[0][j] = 0;
        dp[0][0]=1;
        for(int i=1;i<=n;i++){
            int num=nums[i-1];//索引为i（从1开始）
            for(int j=0;j<=target;j++){
                if(j<num)
                    dp[i][j]=dp[i-1][j];
                else{
                    dp[i][j]=dp[i-1][j]+dp[i-1][j-num];
                }
            }
        }
        return dp[n][target];
    }
};

一维数组：

1.状态定义:
dp[j]为恰好能凑满目标值为j的背包方案数

2.状态转移:
背包容量能或者不能装下nums[i]
（1）当不能装下nums[i]时, 方案数直接继承之前的dp[j]
dp[j]=dp[j];

（2）当能装下nums[i]时, 方案数= 不考虑nums[i]的方案数 + 有nums[i]参与新增的方案数
dp[j]=dp[j]+dp[j-num[i]];

3.状态初始化:
dp[0]=1,因为后面总会一直查找至j=0,如dp[3] += dp[3-3],空集是任意一条有效路径的起点,当属一条

4.遍历顺序:
i正序,j倒序

5.返回形式:
dp[target]就是凑成target的总的方案数

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int n=nums.size();
        int sum=accumulate(nums.begin(), nums.end(), 0);
        if(sum<target || (sum+target)%2==1){
            return 0;
        }
        //转化为01背包后的目标值
        target=(target + sum)/2;
        if(target<0)
            return 0;
        vector<int> dp(target+1,0);
        //边界
        dp[0]=1;
        for(int i=1;i<=n;i++){
            int num=nums[i-1];//索引为i（从1开始）
            for(int j=target;j>=num;j--){
                if(j<num)
                    dp[j]=dp[j];
                else
                    dp[j]=dp[j]+dp[j-num];    
            }
        }
        return dp[target];
    }

};

完全背包最值问题

零钱兑换

322. 零钱兑换
二维dp：
dp[i][j]:用前i个给定硬币能换到面值为j的最小硬币数量

class Solution {
public:
    int coinChange(vector<int> &coins, int amount){
        //给dp数组每个位置赋初值为Max是为了最后判断是否能填满amount
        int n=coins.size();
        int Max=amount+1;
        vector<vector<int>> dp(n+1,vector<int>(amount+1, Max));
        dp[0][0] = 0;  
        for (int i=1;i<=n;i++){
            dp[i][0]=0;
        }
        for (int i=1;i<=n;i++){
            int coin=coins[i-1];
            for (int j=1; j<=amount; j++){
                if(j>=coin)
                    dp[i][j] = fmin(dp[i-1][j], dp[i][j - coin] + 1);
                else{
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[n][amount] == Max ? -1 : dp[n][amount];
    }

};

一维dp：
dp[j]:换到面值j所用的最小硬币数量

class Solution {
public:
    int coinChange(vector<int> &coins, int amount){
        //给dp数组每个位置赋初值为INT_MAX是为了最后判断是否能填满amount
        //要用long long 类型
        int n=coins.size();
        vector<long long> dp(amount+1, INT_MAX); 
        //dp[i]:换到面值i所用的最小数量
        dp[0] = 0;  
        for (int i=1;i<=n;i++){
            int coin=coins[i-1];
            for (int j = 1; j <= amount; j++){
                if(j>=coin)
                    dp[j] = fmin(dp[j], dp[j - coin] + 1);
            }
        }
        return dp[amount] == INT_MAX ? -1 : dp[amount];
    }
};

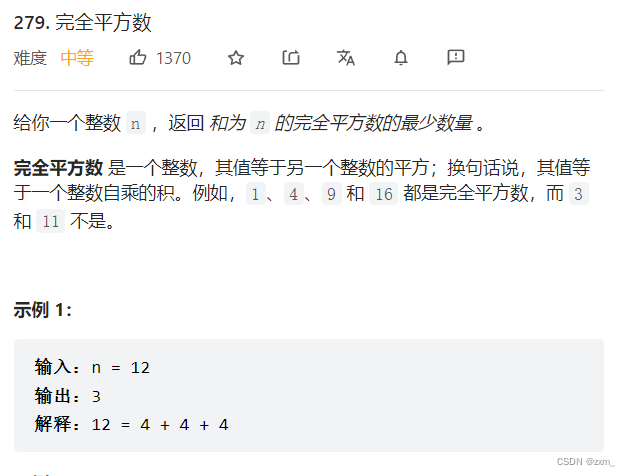
完全平方数

279. 完全平方数
在这里插入图片描述

二维dp：
dp[i][j]:用[1-i]个整数的平方数 能凑到 和为j 的最小整数个数

class Solution {
public:
    int numSquares(int n){
        vector<vector<int>> dp(sqrt(n)+1,vector<int>(n+1, INT_MAX)); 
        dp[0][0]=0;
        for(int i=0;i<=sqrt(n);i++){
            dp[i][0]=0;
        }
        for (int i=1; i<=sqrt(n); i++){
            int num=i*i;
            for (int j=1; j<=n; j++){
                if(j>=num)
                    dp[i][j] = fmin(dp[i-1][j], dp[i][j - num] + 1);
                else
                    dp[i][j]=dp[i-1][j];
            }
        }
        return dp[sqrt(n)][n];
    }

};

一维dp：
dp[j]:用[1-sqrt(n)]个整数的平方数 能凑到 和为j 的最小整数个数

class Solution {
public:
   int numSquares(int n){
       //dp[i]:和为i的完全平方数的最小数量
        vector<int> dp(n + 1, INT_MAX); 
        dp[0] = 0;
        for (int i = 1; i <= sqrt(n); i++){
            int num=i*i;
            for (int j = 1; j <= n; j++){
                if (j >= num)
                    dp[j] = min(dp[j], dp[j-num]+1);
            }
        }
        return dp[n];
    }
};
zxm_
关注
  • 1
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
Leetcode:LeetCode 刷题总结
05-11
5. **动态规划**：动态规划是一种解决问题的方法，通过将问题分解成更小的子问题来求解。如"背包问题"（Knapsack Problem）或"最长公共子序列"（Longest Common Subsequence）。 6. **回溯法**：回溯法通常用于解决...
c++算法----动态规划（背包专题）
qq_63763951的博客
05-02 3496
1.普通背包问题 2.完全背包问题 3.多重背包问题 1.普通背包问题 每到第i个位置就考虑是否拿第i个位置上的物品（当然也要考虑当前背包的体积是否能装得下这个物品），以此类推，直至到达最后一个物品的位置。 #include <iostream> #include <algorithm> using namespace std; /* * 有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。 *第 i 件物品的体积是 vi，价值是 wi。 *...
动态规划之背包问题（C/C++）
qq_41255687的博客
04-12 733
动态规划之背包问题（C/C++） 本文仅代表我个人查阅资料后，对于背包问题的理解，文中如有不好或者不对的地方欢迎指正。 1.0-1背包问题 1.1 问题描述 给定N个物品,每个物品有一个重量W和一个价值V.你有一个能装M重量的背包.问怎么装使得所装价值最大.每个物品只有一个. 1.2问题分析 从这个问题中是给定了一个容量没M的背包，和N个重量为W和价值为V的物品，我要用这N个物品是填充背包使，...
动态规划：背包问题模板代码汇总
qq_60256199的博客
07-22 837
dp背包问题模板代码汇总：acwing算法基础课，acwing算法提高课。
动态规划」详解背包问题及实践（附C++代码）
BXA
05-10 4839
背包问题是一个经典的组合优化问题，它可以被抽象为一个把物品放入背包中的过程，以求最终背包中物品价值的最大化。0/1背包问题是一个经典的动态规划问题，指的是有n个物品和一个容量为W的背包，每个物品只能选择装入一次或不装入。在装入背包的物品总重量不能超过W的前提下，选择物品装入背包中，使得背包中物品的总价值最大。
leetcode316-leetcode_and_swordoffer:LeetCode分类题解，语言为C++
06-30
LeetCode、剑指Offer刷题笔记(C++实现) LeetCode 题目按类型分类 Hash 链表 双指针 快慢指针 滑动窗口 区间合并 字符串操作 数字操作 数组操作 栈 单调栈 堆 递归 分治/二分查找 动态规划 树形DP 0-1背包 [474_一和...
C++ LeetCode刷题班.zip
04-22
在本课程中，"C++ LeetCode刷题班.zip"，我们的目标是深入学习和实践C++编程语言，特别是聚焦于数据结构与算法的应用，这对于准备面试，尤其是BAT（百度、阿里巴巴、腾讯）等知名互联网公司的面试至关重要。...
leetcode_101：LeetCode 101：和你一起你轻松刷题（C ++）
02-05
- **动态规划**：LeetCode上的许多复杂问题可以通过动态规划求解，如背包问题、最长公共子序列等。 - **图论**：包括最短路径算法（Dijkstra、Floyd-Warshall）、拓扑排序等。 - **回溯法**：用于解决组合优化...
算法-动态规划-背包问题-C++
weixin_43541510的博客
03-22 756
在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。
C++ DP算法，动态规划——背包问题（背包九讲）
小天狼星_布莱克 的博客
01-28 2335
有N件物品和一个容量为V的背包。放入第i件物品耗费的空间是Ci​，得到的价值是Wi​。求解将哪些物品装入背包可使价值总和最大。有N件物品和一个容量为V的背包。放入第i件物品耗费的空间是Ci​，得到的价值是Wi​。求解将哪些物品装入背包可使价值总和最大。有N件物品和一个容量为V的背包。放入第i件物品耗费的空间是Ci​，得到的价值是Wi​。求解将哪些物品装入背包可使价值总和最大。有N件物品和一个容量为V的背包。放入第i件物品耗费的空间是Ci​，得到的价值是Wi​。求解将哪些物品装入背包可使价值总和最大。有N件物
【动态规划】背包问题的C++求解
最新发布
V123456789987654的博客
07-11 159
【动态规划】背包问题的C++求解
背包问题代码合集（C/C++）
m0_71934846的博客
02-11 5852
背包问题代码合集（C/C++）
动态规划——完全背包问题（C++实现）
Elon15的博客
11-21 2119
动态规划——完全背包问题（C++实现）
动态规划——01背包问题（C++实现）
Elon15的博客
11-07 6088
动态规划——01背包问题（C++实现）
动态规划之01背包和完全背包问题（力扣C++题解）
lihua777的博客
02-04 1120
强烈推荐代码随想录！！！（纯路人）
C++刷题笔记(38)——完全背包、多重背包、leetcode518、377、70、322、279、139
STATEABC的博客
06-02 266
完全背包理论基础 多重背包理论基础 题目1：518.零钱兑换Ⅱ 题目2：377.组合综合Ⅳ 题目3：70.爬楼梯 题目4：322.零钱兑换 题目5：279.完全平方数 题目6：139.单词拆分
leetcode 1049.最后一块石头的重量Ⅱ 动态规划背包问题求解 （c++版本）
weixin_45748989的博客
11-23 356
leetcode 1049.最后一块石头的重量Ⅱ 动态规划背包问题求解 （c++版本）
leetcode刷题之背包问题（01背包）
mabaizi的博客
02-09 3971
最简单的背包
leetcode刷题，C++刷题技巧
11-08
在《LeetCode刷题，C++刷题技巧》这个资源中，作者高畅ChangGao分享了他刷LeetCode的经验和技巧，特别针对C++编程者。书中的内容被划分为算法和数据结构两大领域，共十五个章节，涵盖了LeetCode中常见的问题类型。...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值