将树转化为二叉树表示

二叉树在数据结构的重要性是因为所有的树都可以通过简单的转换，而称为一棵二叉树。

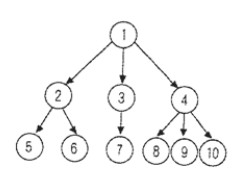
一般的树，每个结点都会有n个分支，这样处理起不同的分支的树都需要重新设计一套操作方案，而且空指针的问题会比二叉树更加的严重。来看一个例子，如下一颗树

如果需要将上图的树转换为二叉树，也就是由N个分支转换为2个分支。我们可以把每一个拥有同一父节点的子节点，也就是兄弟结点向右连接起来。保留最左边的父子连接，将其他的父子连接都打断，这时就可以产生一棵新的二叉树。
如图

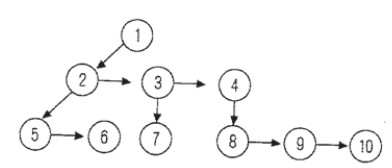
调整一下

---

简单叙述一下过程

1. 1是根结点2、3、4是兄弟结点，则保留最左边的2结点其与1为父子关系，2是1的左孩子。将34结点依次链接到2结点的右边。
2. 5、6是2的子结点，5、6为兄弟结点，则保留最左边的5结点与2为父子关系，5是6的左孩子，6结点链接在5结点的右边
3. 7是3的子结点，7没有兄弟结点，则保留7结点与3结点的父子关系。7是3的左孩子
4. 8、9、10是4结点的子结点，8、9、10为兄弟结点，则保留最左边的8结点与4为父子关系，8是4的左孩子，910结点依次连接在8结点的右边
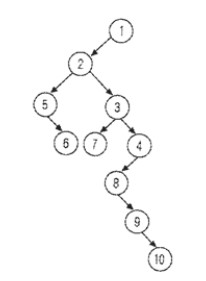
5. 二叉树转换完毕。