Codeforces Round #500 (Div. 2) [based on EJOI]

最新推荐文章于 2020-11-02 21:07:48 发布

总想玩世不恭

最新推荐文章于 2020-11-02 21:07:48 发布

阅读量190

点赞数

分类专栏：算法竞赛

本文链接：https://blog.csdn.net/zxwsbg/article/details/81902524

版权

算法竞赛专栏收录该内容

166 篇文章 3 订阅

订阅专栏

链接：http://codeforces.com/contest/1013

无聊做着玩的。

A.Piles with stones

傻逼题

B.And

题目

输入n和x

给定一个数列，如果一个数列至少出现两个一样的数，那么就符合条件。

当然了，还可以进行操作，比如把 a[i] 替换成 a[i]&x ，这样的操作可以进行无限多次。

输出使数列符合条件需要进行的最小操作的次数。

题解

很简单的一道题。总共就4种情况：

随你怎么换永远不符合条件，输出-1；
不用换，本来就符合条件，输出0；
需要替换掉一个数，使其与另一个没替换的相等，输出1；
需要替换掉两个数，替换后的两个数相等，输出2；

代码

#include <bits/stdc++.h>
using namespace std;

#define INIT(x) memset(x,0,sizeof(x))
#define eps 1e-8

typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 200005;

inline void read(int &x)
{
    int f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}

inline void print(int x)
{
    if(x<0){ putchar('-'); x=-x;}
    if(x>9) print(x/10);
    putchar(x%10+'0');
}

inline void caltime(int tt) {
	tt = clock() - tt;
    cerr << (double)tt/CLOCKS_PER_SEC << " seconds!" << endl;
}

int n,x;
int a[maxn];
map<int,int> mp;
set<int> s1,s2;

int main()
{
	cin>>n>>x;
	for(int i=0;i<n;i++) {
		read(a[i]);
		mp[a[i]]++;
	}
	if(mp.size()<n) {
		cout<<0;
		return 0;
	}
	int temp = 0;
	for(int i=0;i<n;i++) {
		int k = a[i]&x;
		s2.insert(k);
		if(k==a[i])	continue;
		if(mp[k]==1) {
			cout<<1<<endl;
			return 0;
		}
	}
	if(s2.size()<n)	{
		cout<<2;
		return 0;
	}
	cout<<-1<<endl;
	return 0;
}

C.Photo of The Sky

题目

输入一个n，然后给出2*n个数，要求把这2*n个数任意两两组合，形成n个点对，把这些点对放在坐标系中。要求围住它们的矩形面积最小，求这个面积。

题解

首先可以先给数组排个序。然后可以想到，一种解法的两个端点分别为(a[1],a[n],)和(a[n+1],a[2n])这样显然是符合题意的，但是却不一定是最优的，因为可能出现高和宽都很短，但由于正方形面积最大，使得它们的面积反而大了。例如1,1,2,3,4,4,4,6。

于是，还有种思路，就是x轴的两端分别为a[1]和a[2n],高度的两段为a[i+1]和a[n+i],这样高度上正好保证有n个点组成纵坐标，且一定符合题意。

代码

#include <bits/stdc++.h>
using namespace std;

#define INIT(x) memset(x,0,sizeof(x))
#define eps 1e-8

typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 200005;

int n;
ll f[maxn];

ll solve(ll a,ll b,ll c,ll d) {
	return abs(c-a)*abs(d-b);	
}

int main()
{
	cin>>n;
	for(int i=1;i<=2*n;i++) {
		scanf("%lld",&f[i]);
	}
	sort(f+1,f+2*n+1);
	ll ans = solve(f[1],f[n+1],f[n],f[2*n]);
	for(int i=1;i<n;i++) {
		ans = min(ans,solve(f[1],f[i+1],f[2*n],f[i+n]));
	}
	cout<<ans<<endl;
	return 0;
}

D.Chemical table

题意

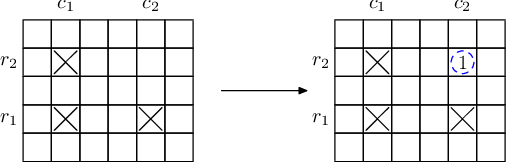三个格子的元素可以生出一个格子的元素。

现在已知有若干个有元素的格子，问最少需要多少个元素，能把所有的都填满。（新生出来的元素不能再生，但是老元素可以用多次）

题解

我们可以用行和列做标记，如果一行已经有了一个元素，那么该元素所处的行和列都加标记。这样就出现了一个问题，如果两个元素在对角，那么不需要三个元素就会自动生成两个，这显然是不符合题意的。

于是，我们用vector记录某一行上的点和哪些列想连，某一列上的点和哪些行相连。

可以看作一个并查集，依次遍历每一行，把改行所有能到的地方都加标记。对于之前说的那种情况，由于不联通，所以不能一次遍历完，要2次，所以原图可以分为两个块。

代码

#include <bits/stdc++.h>
using namespace std;

#define INIT(x) memset(x,0,sizeof(x))
#define eps 1e-8

typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 200005;

inline void read(int &x)
{
    int f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}

inline void print(int x)
{
    if(x<0){ putchar('-'); x=-x;}
    if(x>9) print(x/10);
    putchar(x%10+'0');
}

inline void caltime(int tt) {
	tt = clock() - tt;
    cerr << (double)tt/CLOCKS_PER_SEC << " seconds!" << endl;
}

int n,m,q;
vector<int> e[maxn*10];
bool vis[maxn*10];

void dfs(int x)
{
	vis[x] = 1;
	for(int i=0;i<e[x].size();i++) {
		if(!vis[e[x][i]])
			dfs(e[x][i]);
	}
}

int main()
{
	cin>>n>>m>>q;
	for(int i=0;i<q;i++) {
		int x,y;
		read(x),read(y);
		e[x].push_back(y+n);
		e[y+n].push_back(x);
	}
	int ans = 0;
	for(int i=1;i<=m+n;i++) {
		if(!vis[i]) {
			dfs(i);
			ans++;
		}
	}	
	cout<<ans-1<<endl; //结果是ans-1，如果原图只有1个块，那么就不用增加；需要自己添加的空白格子每个都单独形成一个块
	return 0;
}