算法导论（三版）：第二章第三节课后题

第二章：算法基础
第三节：设计算法

2.3-1

Using Figure 2.4 as a model, illustrate the operation of merge sort on the array A={3; 41; 52; 26; 38; 57; 9; 49}.

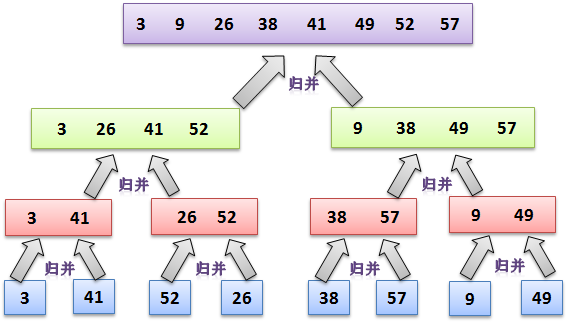
excel已经存网盘：CLRS_exercises_2.3-1

2.3-2

Rewrite the MERGE procedure so that it does not use sentinels, instead stopping once either array L or R has had all its elements copied back to A and then copying the remainder of the other array back into A.
答：
代码如下：

#!/usr/bin/env python
# -*- coding: utf8 -*-
"""
brief:算法导论(三版)的练习题2.3-2
author:zhangyang27@baidu.com
"""
import doctest


def merge(a,b):
    """
    归并算法的merge过程，要求不用哨兵完成。
    写完之后发现不用哨兵，确实代码量要多写几行
    Example
    -------
    >>> merge('1 5 10 15','2 6 11')
    '1 2 5 6 10 11 15'
    >>> merge('1 5 10 15','2 5 11')
    '1 2 5 5 10 11 15'
    >>> merge('','2 5 11')
    '2 5 11'
    >>> merge('','')
    ''
    """
    output = []
    list_a = a.split()
    list_b = b.split()
    a_len = len(list_a)
    b_len = len(list_b)
    i = j = 0
    while i < a_len and j < b_len:
        if int(list_a[i]) < int(list_b[j]): #被坑了好久，才发现不加int()也可以比较，但是是按str来比较的
            output.append(list_a[i])
            i += 1
        else:
            output.append(list_b[j])
            j += 1

    if i >= a_len:
        while j < b_len: #可以不用while循环，可以用python的list截取,但是为了脱离于语言，这样的while循环更好
            output.append(list_b[j])
            j += 1
    else:
        while i < a_len:
            output.append(list_a[i])
            i += 1

    return " ".join(output)

def main():
    doctest.testmod()


if __name__ == '__main__' :
    main()

2.3-3

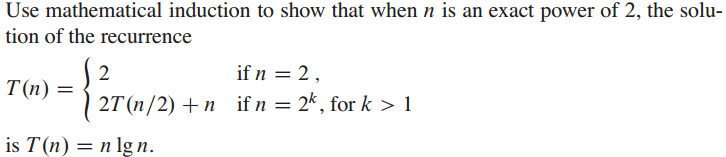
答：

2.3-4

We can express insertion sort as a recursive procedure as follows. In order to sortA[1…n], we recursively sort A[1…n-1] and then insert A[n] into the sorted arrayA[1 … n-1] . Write a recurrence for the running time of this recursive version of insertion sort.
答：

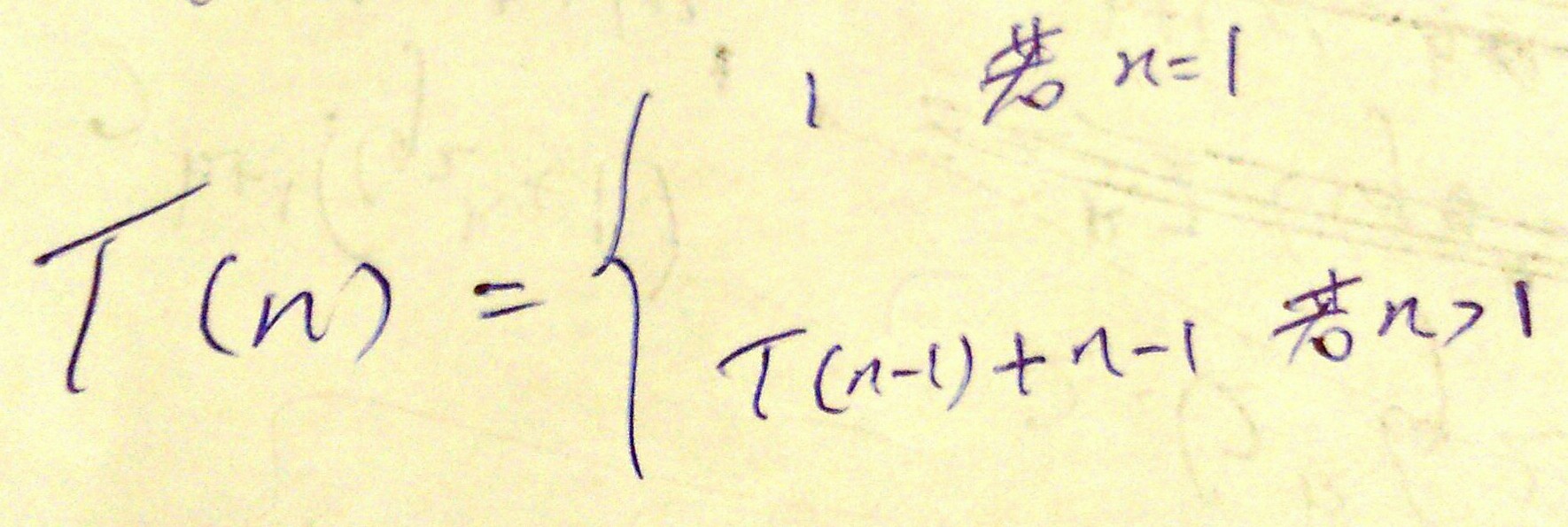
其中 T(n-1) + n - 1的 n-1是指：当为第n个元素寻找该插入的位置的时候，除了需要前n-1个元素有序（T(n-1)），还需要第n个元素和前n-1个元素比较（最坏的情况下）。

2.3-5

Referring back to the searching problem (see Exercise 2.1-3), observe that if the sequence A is sorted, we can check the midpoint of the sequence against and eliminate half of the sequence from further consideration. The binary search algorithm repeats this procedure, halving the size of the remaining portion of the sequence each time. Write pseudocode, either iterative or recursive, for binary search. Argue that the worst-case running time of binary search is θ(lgn).

答：
python代码如下：

#!/usr/bin/env python
# -*- coding: utf8 -*-
"""
brief:算法导论(三版)的练习题2.3-5
author:zhangyang27@baidu.com
"""
import doctest


def binary_search(a,x,l,r):
    """
    在数组a的下标范围为l至r内进行二分查找x,有则返回数组a下标，无则返回 None
    (下面第五个测试永烈，在使用doctest的时候，返回None就什么也不要写)
    Example
    -------
    >>> binary_search('1 2',3,0,1)

    >>> binary_search('1 2',2,0,1)
    1
    >>> binary_search('1',1,0,0)
    0
    >>> binary_search('1 2 3 4 5 6 7 8 9 10',5,0,9)
    4
    >>> binary_search('1 2 3 4 5 6 7 8 9 10 11 12',10,0,11)
    9
    >>> binary_search('1 2 3 4 5 6 7 8 9 10 12',11,0,10)

    """
    if l > r:
        return None

    list_a = a.split()
    mid = l + ( (r-l) / 2 )

    if int(list_a[mid]) == x:
        return mid

    if int(list_a[mid]) < x:
        return binary_search(a,x,mid+1,r)
    else:
        return binary_search(a,x,l,mid-1)

def main():
    doctest.testmod()

if __name__ == '__main__' :
    main()

下面证明其在最坏的情况下的时间复杂度是：θ(lgn)

• 首先，根据代码写出递归式
• 利用递归式画出递归树，求解其时间复杂度（过程与书中图2-5类似）

递归式如下：
　　　 / 1　　　　　　　 当 l > r
T(n) = |
　　　＼T(n/2 - 1) + c 　 当 l <= r

解释一下，其中c是指在每次函数调用的常量操作。

下面是递归树，为了方便分析，我觉得可以将上面T(n/2 - 1)简化为T(n/2)

递归调用  每层代价   层高
T(n)      c ----------┳-
 ↓       ↓           │  
T(n/2)    c           │         
 ↓       ↓           ↓
T(n/4)    c           lgn
 ↓       ↓           ↑
 ┇       ┇           │
 ↓       ↓           │
 1        1 ----------┻-

由上图可以知道 ，将每层代价和层高相乘可以得：clgn+1
由于到了最底层，就是最坏的情况，知道最后都没有查找到元素。故可以知道clgn+1 = θ(lgn)。

2.3-6

Observe that the while loop of lines 5–7 of the INSERTION-SORT procedure in Section 2.1 uses a linear search to scan (backward) through the sorted subarray A[1… j - 1]. Can we use a binary search (see Exercise 2.3 5) instead to improve the overall worst-case running time of insertion sort to θ(nlgn)

答：
我觉得不能，因为注意看INSERTION-SORT的伪代码：

这不仅仅是一个查找的过程，还有移动元素。即使以二分查找找到了正确的位置，但是还是要移动元素。而移动元素导致了while循环必然产生θ(n)的代价。

2.3-7

Describe a θ(nlgn) time algorithm that, given a set S of n integers and another integer x, determines whether or not there exist two elements in S whose sum is exactly x.
答：
首先穷举一下：
在n个数里面选2个：C(2,n)。再每两个数相加，即可知道是否等于x。
根据书C.2的公式。
C(2,n) = (n!/2!(n - 2)!) = n ( n - 1) = n^2 + n
其时间复杂度为：θ(n^2)，不符合题的要求。

在我一筹莫展之际，突然灵机一动想到一个策略：
对集合S中的每一个数，设为a，如果其大于x，那么另一个需要的数就是x-a(x与a的差值,设为b)。然后在S中查找b即可。
考虑时间复杂度，由于二分查找的时间复杂度为(lgn)，那么最坏的情况对S中每一个数都执行一次查找，共n次。则总共的时间复杂度为(nlgn)。