Quake-III Arena (雷神之锤3)是90年代的经典游戏之一。该系列的游戏不但画面和内容不错,而且即使计算机配置低,也能极其流畅地运行。这要归功于它3D引擎的开发者约翰-卡马克(John Carmack)。事实上早在90年代初DOS时代,只要能在PC上搞个小动画都能让人惊叹一番的时候,John Carmack就推出了石破天惊的Castle Wolfstein, 然后再接再励,doom, doomII, Quake...每次都把3-D技术推到极致。他的3D引擎代码资极度高效,几乎是在压榨PC机的每条运算指令。当初MS的Direct3D也得听取他的意见,修改了不少API。
最近,QUAKE的开发商ID SOFTWARE 遵守GPL协议,公开了QUAKE-III的原代码,让世人有幸目睹Carmack传奇的3D引擎的原码。
这是QUAKE-III原代码的下载地址:
http://www.fileshack.com/file.x?fid=7547
(下面是官方的下载网址,搜索 “quake3-1.32b-source.zip” 可以找到一大堆中文网页的
ftp://ftp.idsoftware.com/idstuff/source/quake3-1.32b-source.zip)
我们知道,越底层的函数,调用越频繁。3D引擎归根到底还是数学运算。那么找到最底层的数学运算函数(在game/code/q_math.c), 必然是精心编写的。里面有很多有趣的函数,很多都令人惊奇,估计我们几年时间都学不完。
在game/code/q_math.c里发现了这样一段代码。它的作用是将一个数开平方并取倒,经测试这段代码比(float)(1.0/sqrt(x))快4倍:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
#ifndef Q3_VM
#ifdef __linux__
assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif
return y;
}
函数返回1/sqrt(x),这个函数在图像处理中比sqrt(x)更有用。
注意到这个函数只用了一次叠代!(其实就是根本没用叠代,直接运算)。编译,实验,这个函数不仅工作的很好,而且比标准的sqrt()函数快4倍!要知道,编译器自带的函数,可是经过严格仔细的汇编优化的啊!
这个简洁的函数,最核心,也是最让人费解的,就是标注了“what the fuck?”的一句
i = 0x5f3759df - ( i >> 1 );
再加上y = y * ( threehalfs - ( x2 * y * y ) );
两句话就完成了开方运算!而且注意到,核心那句是定点移位运算,速度极快!特别在很多没有乘法指令的RISC结构CPU上,这样做是极其高效的。
算法的原理其实不复杂,就是牛顿迭代法,用x-f(x)/f'(x)来不断的逼近f(x)=a的根。
简单来说比如求平方根,f(x)=x^2=a ,f'(x)= 2*x,f(x)/f'(x)=x/2,把f(x)代入
x-f(x)/f'(x)后有(x+a/x)/2,现在我们选a=5,选一个猜测值比如2,
那么我们可以这么算
5/2 = 2.5; (2.5+2)/2 = 2.25; 5/2.25 = xxx; (2.25+xxx)/2 = xxxx ...
这样反复迭代下去,结果必定收敛于sqrt(5),没错,一般的求平方根都是这么算的
但是卡马克(quake3作者)真正牛B的地方是他选择了一个神秘的常数0x5f3759df 来计算那个猜测值
就是我们加注释的那一行,那一行算出的值非常接近1/sqrt(n),这样我们只需要2次牛 顿迭代就可以达到我们所需要的精度.
好吧 如果这个还不算NB,接着看:
普渡大学的数学家Chris Lomont看了以后觉得有趣,决定要研究一下卡马克弄出来的
这个猜测值有什么奥秘。Lomont也是个牛人,在精心研究之后从理论上也推导出一个
最佳猜测值,和卡马克的数字非常接近, 0x5f37642f。卡马克真牛,他是外星人吗?
传奇并没有在这里结束。Lomont计算出结果以后非常满意,于是拿自己计算出的起始
值和卡马克的神秘数字做比赛,看看谁的数字能够更快更精确的求得平方根。结果是
卡马克赢了... 谁也不知道卡马克是怎么找到这个数字的。
最后Lomont怒了,采用暴力方法一个数字一个数字试过来,终于找到一个比卡马克数
字要好上那么一丁点的数字,虽然实际上这两个数字所产生的结果非常近似,这个暴
力得出的数字是0x5f375a86。
Lomont为此写下一篇论文,"Fast Inverse Square Root"。
论文下载地址:
http://www.math.purdue.edu/~clomont/Math/Papers/2003/InvSqrt.pdf
http://www.matrix67.com/data/InvSqrt.pdf
参考:<IEEE Standard 754 for Binary Floating-Point Arithmetic><FAST INVERSE SQUARE ROOT>
最后,给出最精简的1/sqrt()函数:
float InvSqrt(float x)
{
float xhalf = 0.5f*x;
int i = *(int*)&x; // get bits for floating VALUE
i = 0x5f375a86- (i>>1); // gives initial guess y0
x = *(float*)&i; // convert bits BACK to float
x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
return x;
}
大家可以尝试在PC机、51、AVR、430、ARM、上面编译并实验,惊讶一下它的工作效率。
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
论文:http://www.daxia.com/bibis/upload/406Fast_Inverse_Square_Root.pdf
以上为R的存在说明;
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
以下是R的计算
http://www.guokr.com/post/91389/
基础知识1:i>>1
操作i>>1表示将二进制数i向右移动一位,也就是将最后一位删掉并在最前一位添加0
注意到我们将一个n位的十进制数M删掉最后一位之后就变成了n-1位,可以看做将这个十进制数除以10之后向下取整floor(M/10)
同样的,讲一个二进制数删掉最后一位之后相当于将这个数除以2并向下取整floor(M/2)
这样看上去i>>1就像是floor(i/2),因为函数f(x)=1/sqrt(x)的一阶导数是-1/2*(x)^-3/2,正好有个-1/2在前面,不禁让人感觉 0x5f3759df - ( i >> 1 )是函数1/sqrt(x)在某一个点的一阶泰勒展开。在Fast Inverse Square Root 里面有这样一段:
Eberly’s explanation was that this produced linear approximation, but is incorrect; we’ll see the guess is piecewise linear, and the function being approximated is not the same in all cases.
“Eberly的解释是说这相当于做了线性近似,但是这个解释是不对的。我们会看到这个估计值是分段线性的,并且这个近似函数在各种情况下也并不相同。”
为什么这么说呢?这里需要用到基础知识2:浮点数存储方式
各种类型浮点数的存储方式可以通过查看IEEE745(完全不知道是什么东西)了解
这里用到的是32位单精度浮点数,并且总是正数,表示方式为:
0|E|M
其中0代表正数
E是指数,E=0相当于2^-127
M表示一个绝对值小于1的数,但是注意到这里省略了一位。也就是说,当转化位十进制的时候应该表示为(1+M)
那么换算之后的数就应该是:(1+M)2^(E-127)
这样我们发现其实i>>1并不完全是floor(i/2)而是将一个数变成(floor(M/2)+1)*2^floor((E-127)/2)
而且根据E的奇偶性尾数可能还需要加上1/2
不妨令e=E-127,注意到1/sqrt(x)是让原数的指数变为-e/2,这么说来卡马克可能仅仅是希望产生一个e/2而用上了位移,接下来就是要找到一个相减之后产生-e/2并且让尾数尽量和(1+M)^-1/2相近
由于这个数必然为正数假设这个数值为:
0|R1|R2
接下来便是要分情况讨论:
假设E为偶数,这时候指数的右移并不会影响到尾数的数值:
这时候e是奇数,令e=2d+1
那么相减之后指数部分变为:
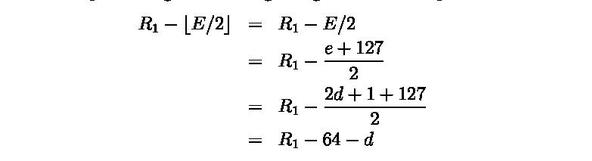
注意这里的相减其实是将浮点数转化为整型(也就是正则化)之后再相减,而不是普通的浮点数加减。
由于初始值一定要是正数,所以我们需要上式一定为正,因为0=<E<=256,所以R1>=128
因为我们讨论的E为偶数,也就是末位数一定是0,所以不用考虑他右移后对M的影响,所以两数相减之后的结果是:

注意这里用M/2而不是floor(M/2)因为这一点点的误差相较于其他误差来说太小了
当然,还存在一种情况,那就是R2<M/2,其实二进制的加减和十进制差不多,如果尾数小了,那么就要像更高位数“借位”,也就是说这种情况下相减之后的结果是:

我们定义:

那么我们可以将这两种情况合并为一个函数:
![]()
这个函数就是我们对函数1/sqrt(x)的近似了,那么我们的目标就是让这个函数的相对误差|(y-y0)/y|尽量小:

这样我们得到一个误差方程:
![]()
之后:

注意这里的1/8其实是凑出来的,具体凑法可以先假设一个小于一的正数a,由于0<R2<1,0<M<1,我们可以通过展开得到R1关于a的一个区间。让a尽量小,使得这个区间范围小于一。根据R1一定是整数的特性,我们可以确定使得误差最小的R1。这里得出R1=190,带入十六进制里面并右移(注意开头有一个表示符号的0)就是0x5f,正好是黑魔法常数的头几位。
那当E为奇数怎么办呢?其实是一样的办法,如果E为奇数,那么M/2就需要加上1/2(尾数的第一位相当于1/2),根据同样的方法,我们可以得到另外一个相对误差函数:
![]()
其中:

有兴趣可以算一算这种情况下R1应该为多少,作者十分偷懒地说由于需要让常数同时应用于两种情况,所以就让R1=190了。
之后就是确定R2的值了,各种分段讨论,过于纠结我们就不看了(反正最后也没算对,摊手),确定下来大约在0.45左右,再通过软件算得最优解。





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








