首先题目是这样的:
剪邮票
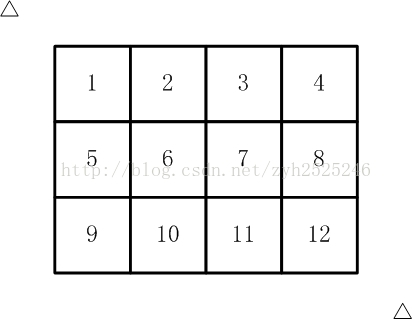
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来,要求必须是连着的。
(仅仅连接一个角不算相连)
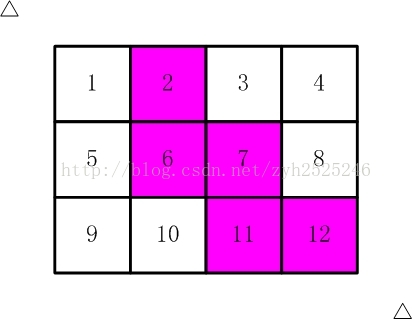
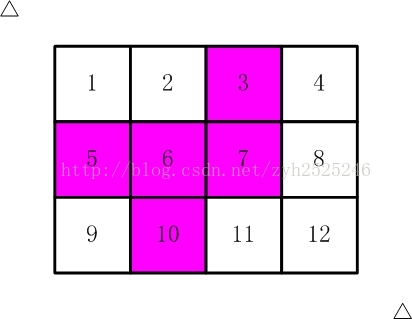
比如,【图2.jpg】,【图3.jpg】中,粉红色所示部分就是合格的剪取。
请你计算,一共有多少种不同的剪取方法。
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
题目要求的是求出所有满足条件的剪法,所以这里就用到组合问题,将所有的可能选出来,再一一进行判断,最终得出结果。
第一步:组合算法
void cbt(int low,int num){ //起始位与需要取出的个数
if (num == 0) { //出口
if (OK(c)) { //判断c数组是否满足条件(代码见下文)
for (int i = 0; i < c.length; i++) {
System.out.print(c[i]+" ");
}
count++;
System.out.println();
}
}else{
for (int i = low; i < a.length; i++) { //组合主体部分
c[num-1] = a[i];
cbt(i+1, num-1);
}
}
}
第二歩:判断条件
这里特殊说明一下,不是所有差值为1的2张邮票都是相连的,好比如4与5,为了防止太多的判断条件,所以将原数值进行修改
1 2 3 4
6 7 8 9
11 12 13 14
这样差值为1则一定在同一行,差值为5则一定在同一列。
boolean OK(int c[]){
boolean b = true; //假定为与其他的邮票相连,若与其他4张邮票均不相连则false
int a[] = new int[5];//定义一个用来放连接数的数组(即该邮票与几张邮票相连)
int temp;//记录邮票相连的个数
for (int i = 0; i < c.length; i++) {
temp = 0;
for (int j = 0; j < c.length; j++) {
if (Math.abs(c[i]-c[j]) == 1||Math.abs(c[i]-c[j]) == 5) {//邮票相连的条件
temp++;
}
}
if (temp == 0) {//如果temp为0 说明与其他4张邮票不相连,则排除(初步判断)
b = false;
}else {//否则就将相连个数记录
a[i] = temp;
}
}
//计算整个数组的相连数总数
int temp2 = 0;
for (int i = 0; i < a.length; i++) {
temp2+= a[i];
}
if (temp2 <= 6) {//如果相连数总数小于等于6,则一定不满足条件(再次判断)
b = false;
}
return b;
}
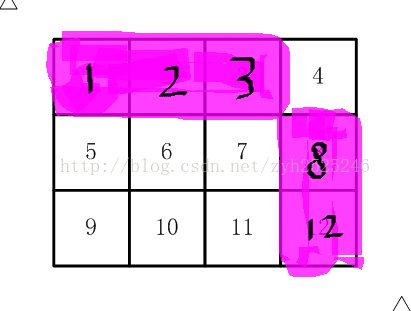
至于为什么第二次的判断条件是小于等于6。
其实很简单,第一次判断过后,唯独只有一种情况没有排除掉,如下图
下面是完整代码:
public class seven {
public static void main(String[] args) {
CBT c = new CBT();
c.cbt(0, 5);
System.out.println(c.count);
}
}
class CBT{
int a[] = {1,2,3,4,6,7,8,9,11,12,13,14};
int c[] = new int[5];
int count = 0;
void cbt(int low,int num){
if (num == 0) {
if (OK(c)) {
for (int i = 0; i < c.length; i++) {
System.out.print(c[i]+" ");
}
count++;
System.out.println();
}
}else{
for (int i = low; i < a.length; i++) {
c[num-1] = a[i];
cbt(i+1, num-1);
}
}
}
boolean OK(int c[]){
boolean b = true;
int a[] = new int[5];
int temp;
for (int i = 0; i < c.length; i++) {
temp = 0;
for (int j = 0; j < c.length; j++) {
if (Math.abs(c[i]-c[j]) == 1||Math.abs(c[i]-c[j]) == 5) {
temp++;
}
}
if (temp == 0) {
b = false;
}else {
a[i] = temp;
}
}
int temp2 = 0;
for (int i = 0; i < a.length; i++) {
temp2+= a[i];
}
if (temp2 <= 6) {
b = false;
}
return b;
}
}
运行结果如下:(部分结果以及总数)







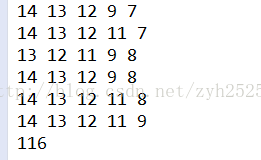














 129
129

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








