支持向量机

最新推荐文章于 2024-05-21 15:39:00 发布

zylyyyyyy

最新推荐文章于 2024-05-21 15:39:00 发布

阅读量746

点赞数 3

文章标签：支持向量机算法机器学习

本文链接：https://blog.csdn.net/zylyyyyyy/article/details/134325229

版权

前言

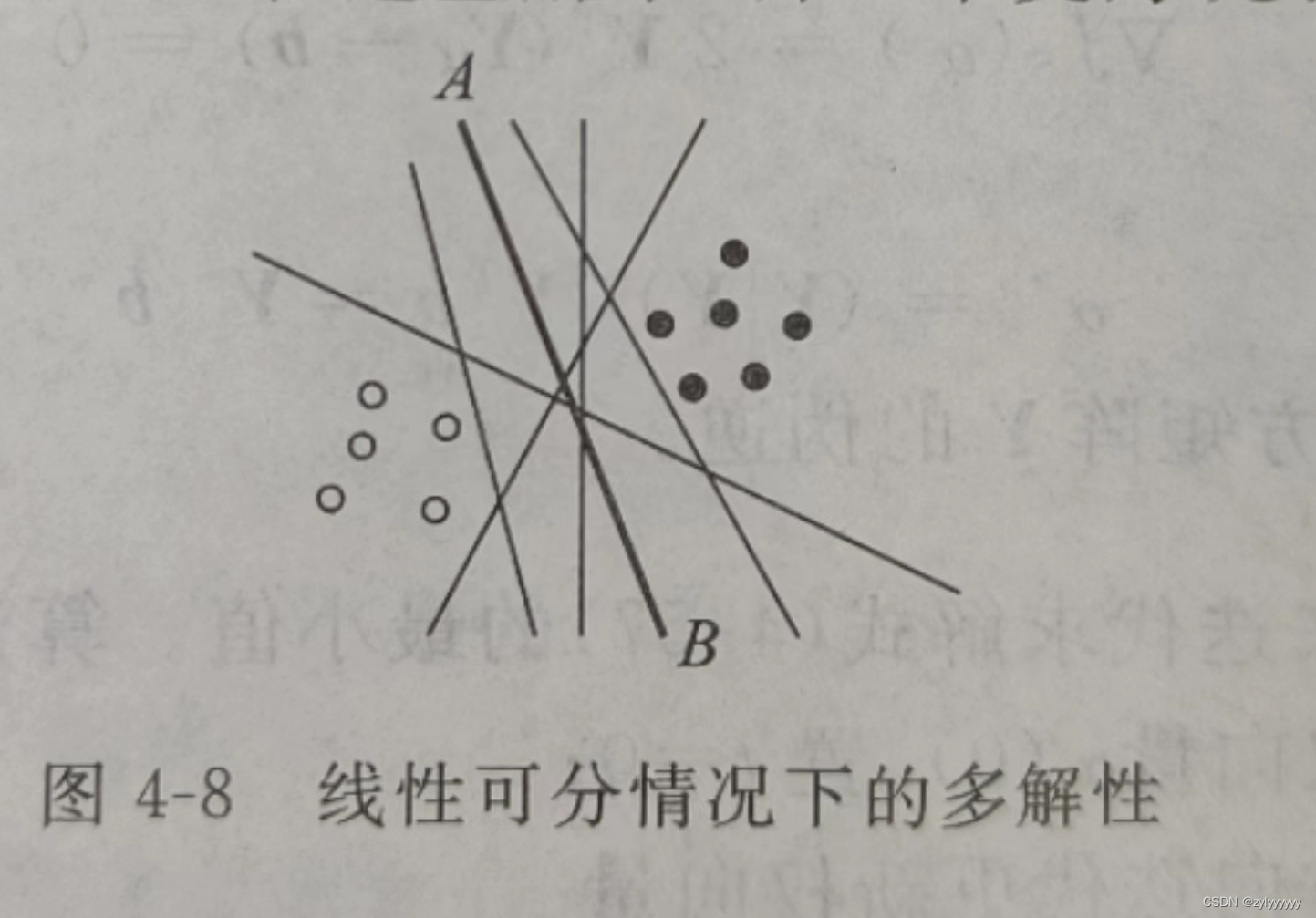
在以前的学习中我们知道，只要一个样本集线性可分，就肯定存在无数多解，解区中任何一个向量都是解向量。感知器算法采用不同的初始值和不同的迭代参数就会得到不同的解，如图 4-8 所示，那么这些解哪一个更好呢？

一、最优分类超平面

1.1 什么是最优超平面

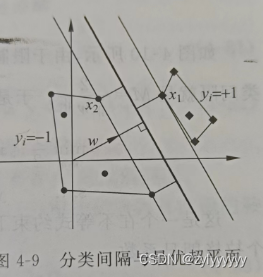
一个超平面，如果它能够将训练样本没有错误地分开,并且两类训练样本中离超平面最近的样本与超平面之间的距离是最大的,则把这个超平面称作最优分类超平面(optimal seperating hyperplane),简称最优超平面(optimal hyperplane)。

两类样本中离分类面最近的样本到分类面的距离称为分类问隔(margin)，最优超平面也称作最大间隔超平面,如图 4-9 所示。

假定有训练样本集
$(x_{1},y_{1}),(x_{2},y_{2}),.......,(x_{n},y_{n})$ , $x_{i}\in R^{d},y_{i}\in \left \{ +1,-1 \right \}$

其中每个样本是d 维向量，y是类别标号， $\omega _{1}$ 类用+1表示, $\omega _{2}$ 类用-1表示。这些样本是线性可分的,即存在超平面
g(x)=(ω·x)+b=0

把所有 N 个样本都没有错误地分开。这里， $\omega \in R_{d}$ 是线性判别函数的权值, b是其中的常数项(在一些书籍中也用ω0表示）。

(ω·x)表示ω与x的内积，也就是 $\omega ^{T}x$ 。

最优超平面的决策函数：

f(x) = sgn(g(x)) = sgn((ω·x)+b)

其中,sgn()为符号函数，当自变量为正值时函数取值为 1,自变量为负值时函数取值为一1。

容易注意到,对于上面的决策函数,对权值 ω和b 作任何正的尺度调整都不会影响分类决策,同时也不会改变样本到分类面的距离，因此上面定义的最优分类面没有唯一解.而是有无数多个等价的解。为了使这一问题有唯一解,需要把 w 和b 的尺度确定下来。

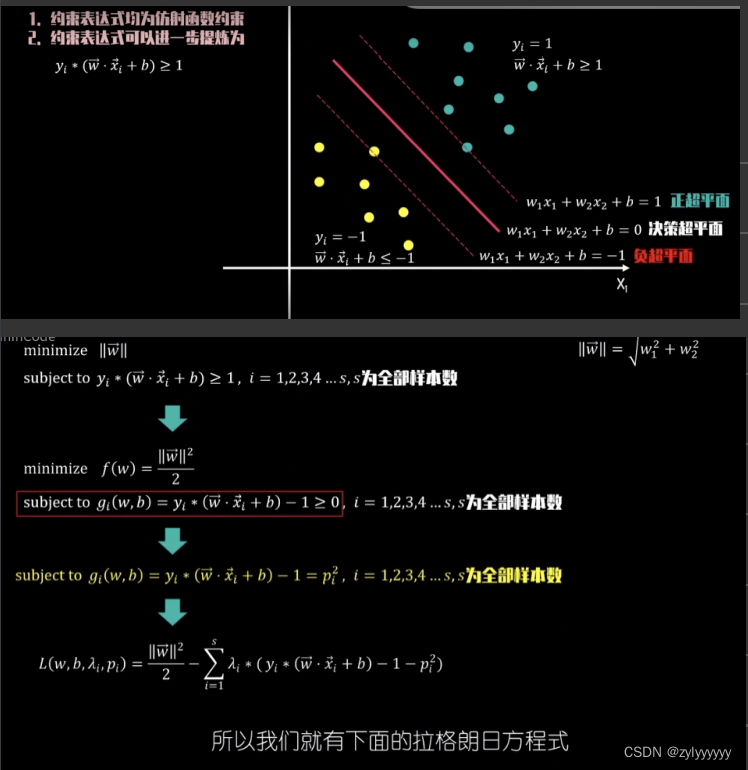
所有 N 个样本都可以被超平面没有错误地分开,就是要求所有样本都满足
$\begin{cases} & \text{(}\omega.xi) +b>0 ,yi =+1\\ & \text{(}\omega.xi) +b<0 ,yi =-1 \end{cases}$
既然尺度可以调整,我们可以把上式的条件变成
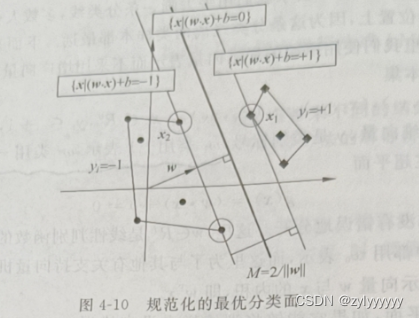
$\begin{cases} & \text{(}\omega.xi) +b\geqslant 1 , yi =+1\\ & \text{(}\omega.xi) +b\leqslant -1 ,yi =-1 \end{cases}$

即要求第一类样本中 g(x)最小等于 1,而第二类样本中 g(x)最大等于-1。g(x) = 1 和 g(x) = -1 就是过两类中各自离分类面最近的样本且与分类面平行的两个边界超平面。

把样本的类别标号 y 值乘到下面的那个不等式，,可以把两个不等式合并成一个统一的形式:

$y_{i}[(\omega .x_{i}) + b]\geq 1$ , i=1,2,...,N

用此条件来约束分类超平面的权值尺度变化，这种超平面称作规范化的分类超平面（the canonical form of the separating hyperplane)。

二、支持向量机

2.1.最优超平面的对偶问题和原问题

2.1.1 推理过程

如上图所示，

由于限制两类离分类面最近的样本的 g(x)分别等于 1 和一1,那么分类间隔就是

$M= \frac{2}{\left \| \omega \right \|}$

于是,求解最优超平面的问题就成为：

$\underset{\omega ,b}{min} \frac{1}{2} ||\omega ||^2$

s.t（约束条件）： yi [(ω·xi)+b] - 1 ≥0 , i=1,2,...,N

这是一个在不等式约束下的优化问题，对每个样本引入拉格朗日系数：

αi ≥ 0 ，i=1,2,...,N

那么上面的优化问题可以转化为下面这个式子：

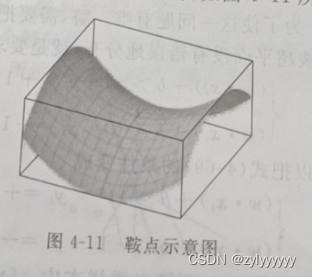
$\underset{\omega ,b} {min} \underset{\alpha}{max} L(\omega ,b,\alpha )= \frac{1}{2}(\omega.\omega) - \sum_{i=1}^{N}\alpha _{i} \{ y_{i}[\omega .x]+b-1\}$

其中 $L(\omega ,b,\alpha )$ 是一个拉格朗日泛函，最优解将在 $L(\omega ,b,\alpha )$ 的鞍点取得。

又因为在鞍点时，目标函数 $L(\omega ,b,\alpha )$ 对ω和b的偏导数都为0，因此我们可以得到在最优解处：

$\omega^{*} = \sum_{i=1}^{N}\alpha_{i}^{*}y_{i}x_{i}$

且

$\sum_{i=1}^{N}y_{i}\alpha_{i}^{*} = 0$

将上面两个条件代入 $\underset{\omega ,b} {min} \underset{\alpha}{max} L(\omega ,b,\alpha )= \frac{1}{2}(\omega.\omega) - \sum_{i=1}^{N}\alpha _{i} \{ y_{i}[\omega .x]+b-1\}$ ，可以得到：

$\underset{\alpha}{max} Q(\alpha )= \sum_{i=1}^{N}\alpha _{i} - \frac{1}{2}\sum_{i,j=1}^{N}\alpha _{i} \alpha _{j}\ y_{i} \ y_{j}(\mathbf{x_{i}.x_{j}})$

s.t. $\sum_{i=1}^{N}y_{i}\alpha_{i}^{*} = 0$ 且 αi ≥ 0 ，i=1,2,...,N

这是一个对αi，i=1,2,...,N的二次优化问题，称为最优超平面的对偶问题。

下式的优化问题称为最优超平面的原问题：

$\underset{\omega ,b}{min} \frac{1}{2} ||\omega ||^2$

s.t（约束条件）： $y_{i}[(\omega .x_{i}) + b] -1 = 0$ , i=1,2,...,N

通过对偶问题的解 $\alpha_{i}^{*}$ ，可以求出原问题的解：

$\omega^{*} = \sum_{i=1}^{N}\alpha_{i}^{*}y_{i}x_{i}$

再利用：

$y_{i}[(\omega ^*.x_{i}) + b^*] -1 = 0$

即可求出ω和b。

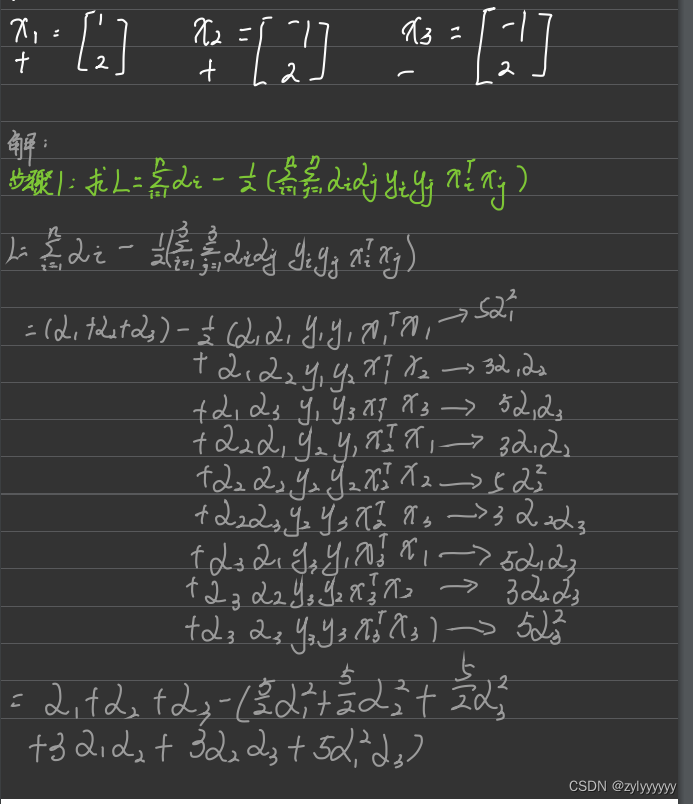
2.求解SVM问题的计算例题

2.2.1 例题一：

2.2.2 例题2

总结

以上就是今天要讲的内容，本文仅仅简单介绍了SVM的数学计算，可以用于对理论考试的辅助。

zylyyyyyy

关注

3
点赞
踩
8

收藏

觉得还不错? 一键收藏
1
评论
支持向量机

在以前的学习中我们知道，只要一个样本集线性可分，就肯定存在无数多解，解区中任何一个向量都是解向量。感知器算法采用不同的初始值和不同的迭代参数就会得到不同的解，如图 4-8 所示，那么这些解哪一个更好呢？一个超平面，如果它能够将训练样本没有错误地分开,并且两类训练样本中离超平面最近的样本与超平面之间的距离是最大的,则把这个超平面称作最优分类超平面(optimal seperating hyperplane),简称最优超平面。
复制链接

扫一扫