计算几何系列 —— 美妙的旋转卡壳算法~上

       本系列文章力求以简洁易懂的文字介绍计算几何中的基本概念，使读者快速入门，故不追求难度和深度，仅起到抛砖引玉的作用。

        不知不觉基础的计算几何就快讲完了，这次我再讲讲有关多边形以及凸包的各种小算法。（QAQ）

     1.旋转卡壳算法

       看到这个算法的时候第一反应是脑子卡壳叭，尤其是我们在做这道家喻户晓的模板题的时候：

             [USACO03FALL] Beauty Contest G /【模板】旋转卡壳 - 洛谷  

          旋转卡壳算法是用来干啥的呢？

        我们将一个多边形上任意两点间的距离的最大值定义为多边形的直径，那么我们如果直接枚举直径所在的两点， 显然太慢了。那么有一个O(n)的算法：旋转卡壳，计算时就像一对平行卡壳卡住凸包旋转而得名，可以说这个名字取得非常的形象，那么我们来看一下这道题目的思路历程：

    先抛出一个问题：

          在二维平面上给定n个点，求距离最远的两个点之间的距离是多少？

      看到这道题，大部分同学第一反应肯定是暴力——暴力枚举所有点对，然后求出最远的那一对相距的距离。这种方法当然没错，可是复杂度已经达到了O(n^2)，当n是50000,100000，甚至1000000时，暴力就显得苍白无力。

      这时我们进一步思考，这个最远点对一定会出现在这些点集的凸包上，所以在这里我们在凸包上，使用复杂度低至O(n)的旋转卡壳算法进行求解。

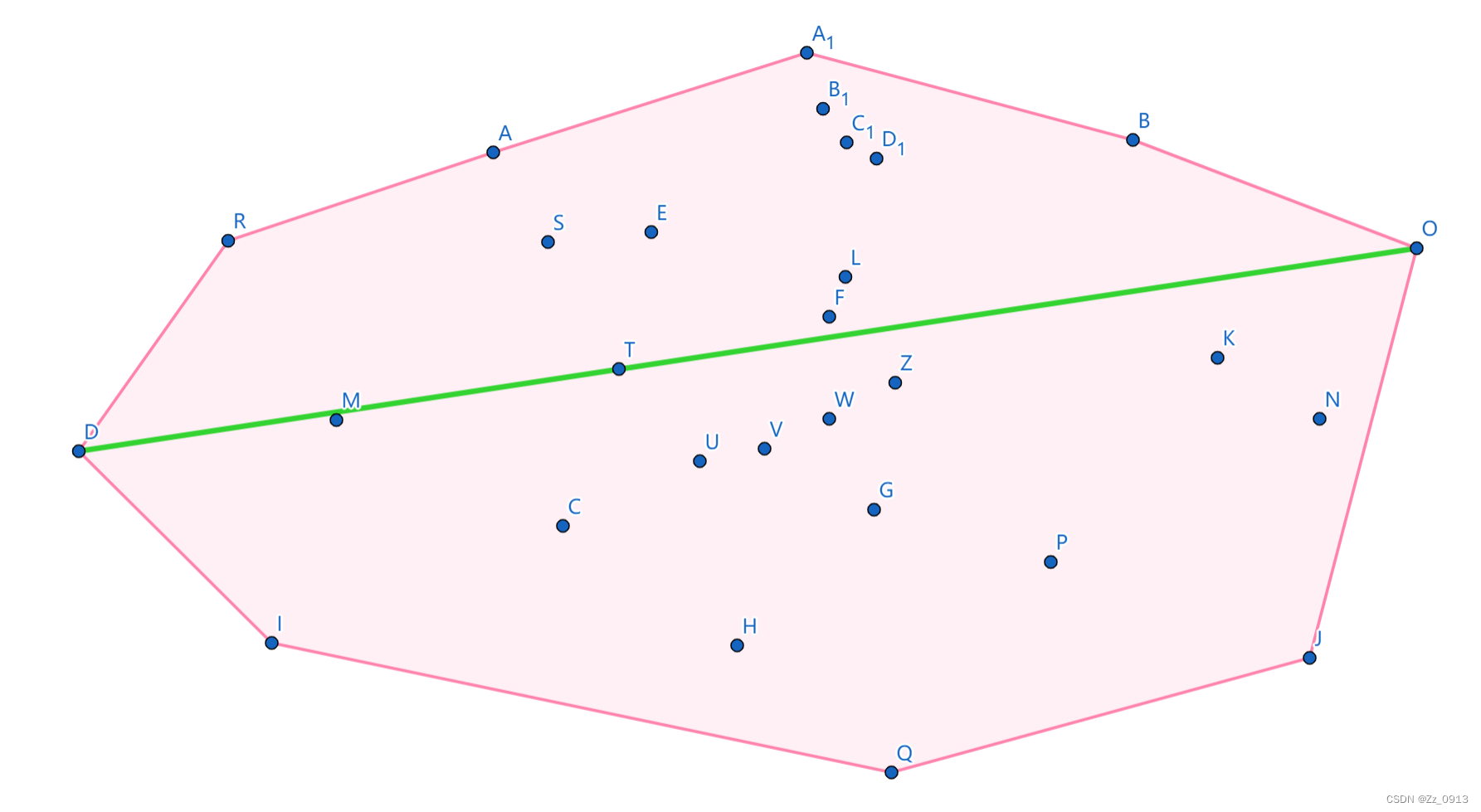
     什么是平行卡壳？非常形象的说法就是卡住凸包的一对平行线，然后旋转卡壳就是让这对平行线旋转起来：

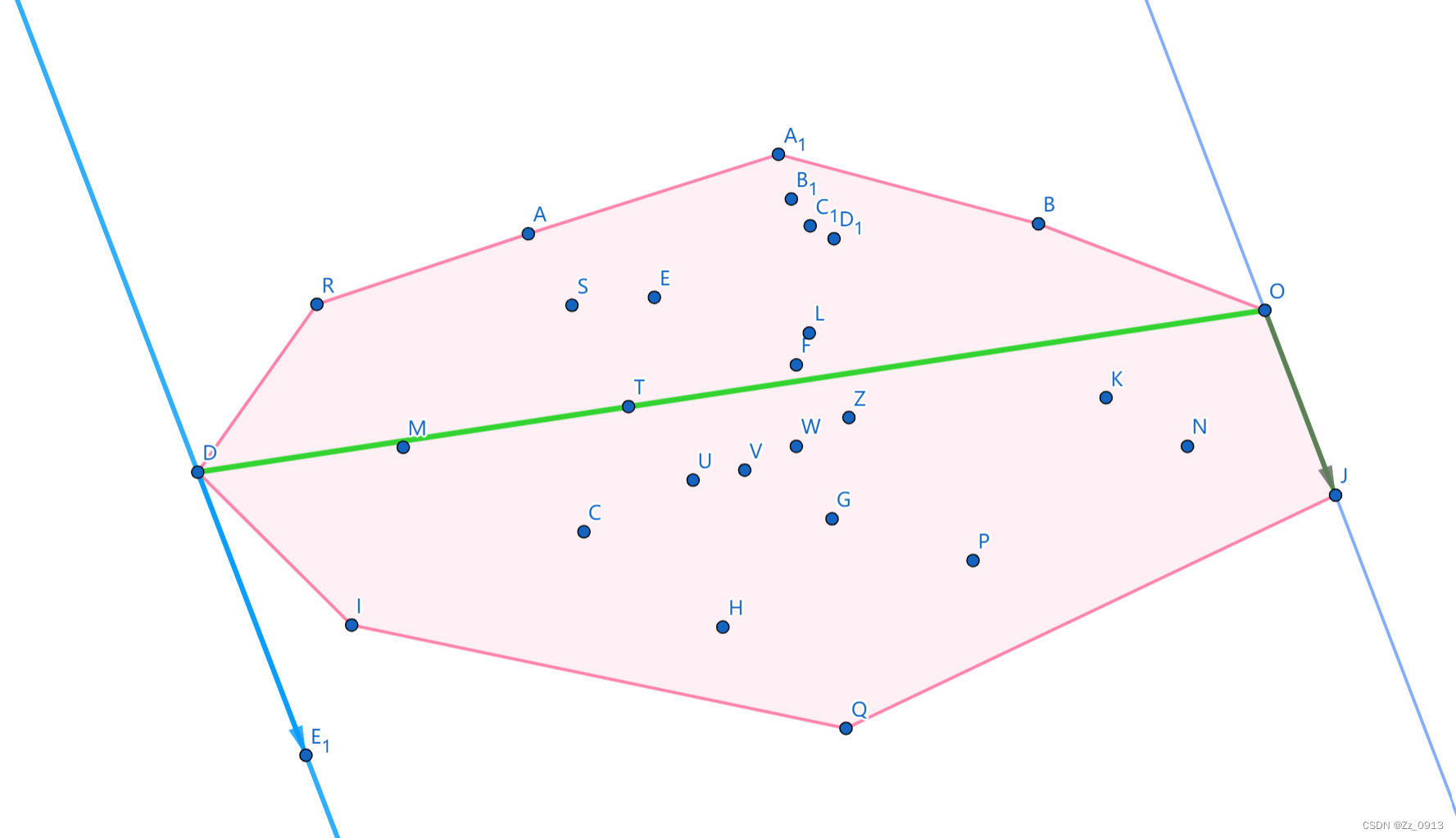
    在凸包上，被一对平行卡壳正好卡住的对应点对称为对踵点；可以证明对踵点的个数不超过3n/2个也就是说对踵点的个数是O(n)的，对踵点的个数也是我们下面解决问题时间复杂度的保证。那么我们来看看旋转卡壳中平行卡壳卡凸包的时候会出现的情况，基本上就是如下两种：

      1.卡住一个点和一条边：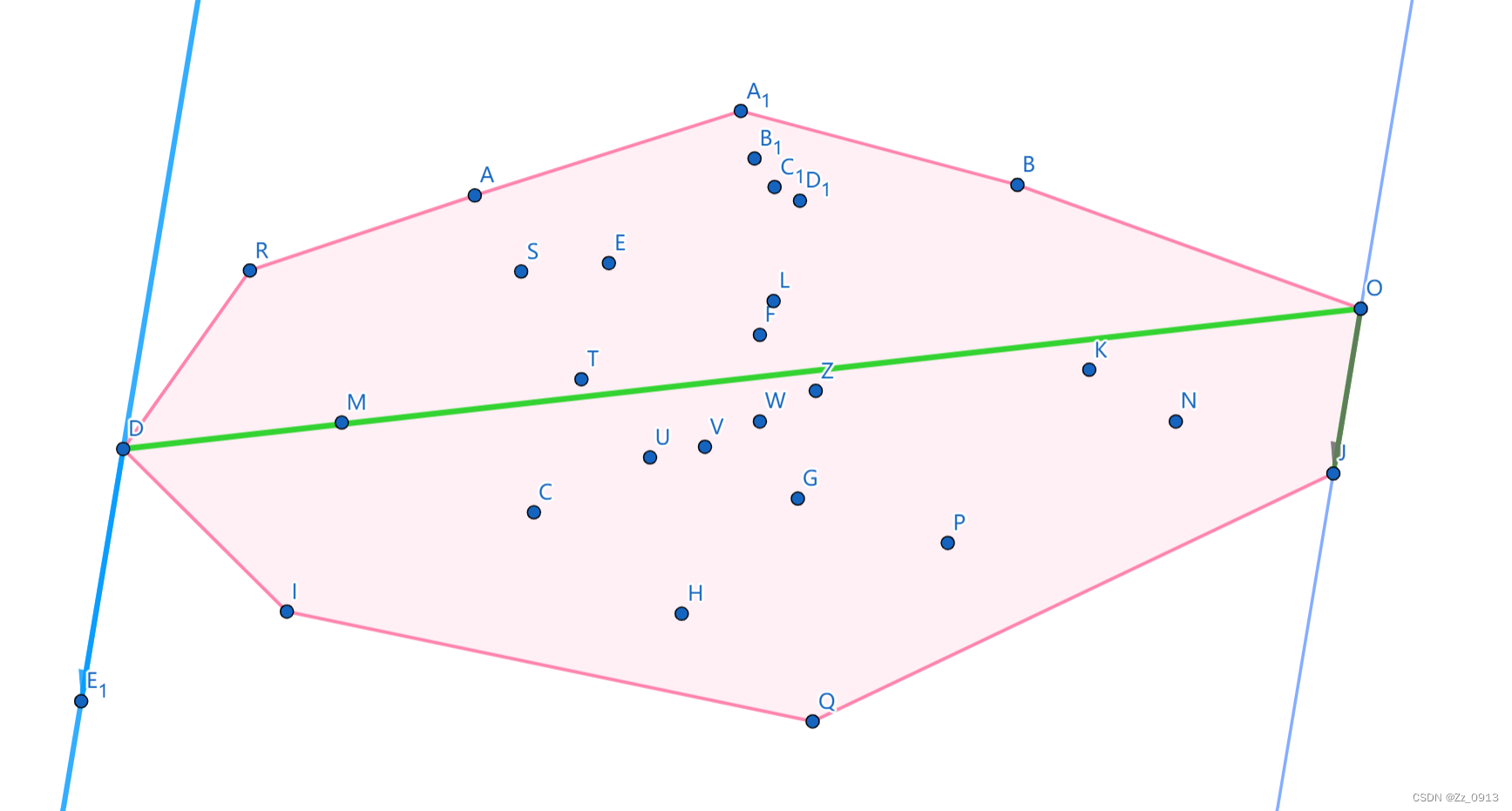

        2.卡住两顶角的两个点：

       由于在处理过程中，卡壳卡住两个点的情况不好处理，所以一般我们都是去关注第一种情况。在这种情况下我们发现，一个对踵点到对应边之间的距离比其他点要大。也就是说，一个对踵点和对应边所形成的三角形的面积是最大的，所以我们可以使用叉积的第二种用法——求三角形面积来求解对踵点。又是叉积~：

     点积&叉积：

        经过比对我们发现，对踵点对距离中的最大值，就是在这个二维平面内两点距离的最大值，总的时间复杂度为O(n)。

   怎样实现旋转卡壳算法？

      1.旋转卡壳算法是建立在二维凸包上的，所以我们先需要对点集求出二维凸包，在之前的文章中已经细讲过了GrahamScan算法。

       有关二维凸包的求解：

             计算几何系列 ——— 结构之美（三角形四心一点，多边形&凸包算法）-CSDN博客

      2.现在我们需要考虑，如何得到距离每条对应边的的最远点呢?稍加分析,我们可以发现,我们可以把点到直线的距离化解为三角形的面积，再运用叉积进行比较。

        同时，凸包上的点依次与对应边产生的距离成单峰函数,面积上升到最高点后，又会下降。(具体证明可以从凸包定义入手用反证法解决)   

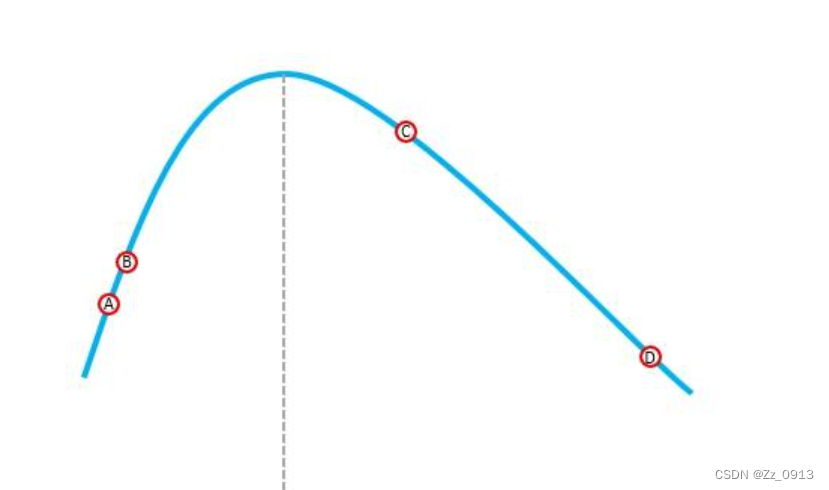
     因此，在求对踵点的过程时，我们采用的是直接枚举，并且利用单峰函数的性质，我们枚举到当下一个点的距离比上一个小的时候我们就停止枚举。  而且随着对应边的旋转，最远点也只会顺着这个方向旋转~，因此，我们可以从上一次的对踵点开始继续寻找这一次的。

     ps:  由于内层while循环的执行次数取决于j增加次数 j最多增加O(n)次，所以求出所有对踵点的时间复杂度为O(n)，对踵点三角形面积求解：

     核心代码：

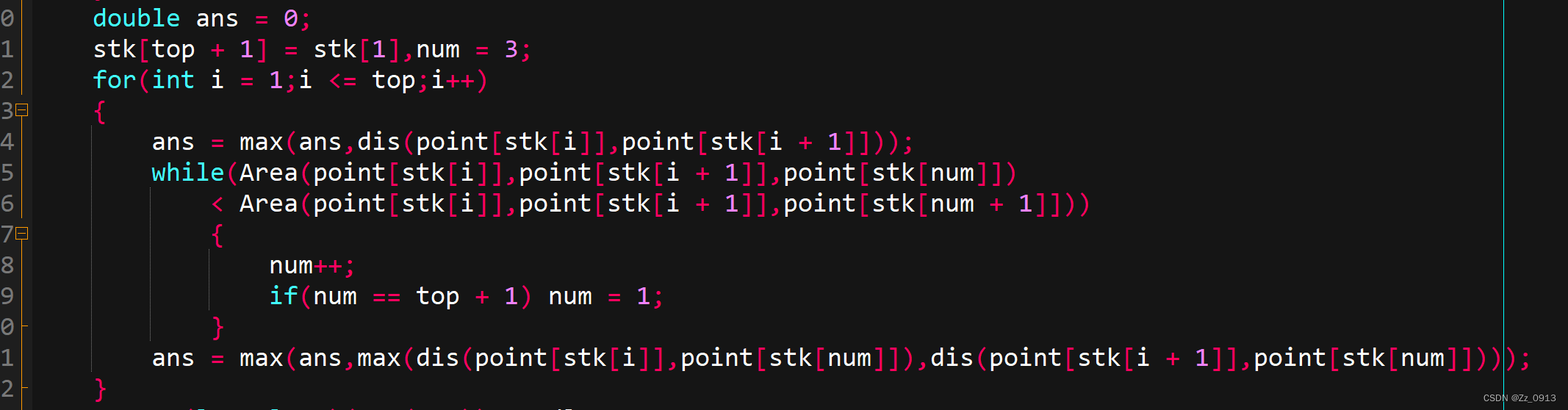
     源代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 1e5 + 20;
const double Eps = 1e-9;
int N,i,top1,stk1[MAXN],top2,stk2[MAXN],top,stk[MAXN],num;
double x,y,js;

#define Temp template<typename T>
Temp inline void read(T &x)
{
	x = 0;
	T w = 1,ch = getchar();
	while(! isdigit(ch) && ch != '-') 
	    ch = getchar();
	if(ch == '-') 
	    w = -1,ch = getchar();
	while(isdigit(ch))
	    x = (x << 3) + (x << 1) + (ch ^ '0'),ch = getchar();
	x = x * w;
}

int Sign(double x) { if(fabs(x) < Eps) return 0;if(x > 0) return 1;if(x < 0) return -1;}

struct Point{
	double x,y;
	Point(double x = 0,double y = 0) : x(x) , y(y) {}
}point[MAXN];

typedef Point Vector;

Vector operator + (Vector Alpha,Vector Beta) { return Vector(Alpha.x + Beta.x,Alpha.y + Beta.y);}

Vector operator - (Vector Alpha,Vector Beta) { return Vector(Alpha.x - Beta.x,Alpha.y - Beta.y);}

Vector operator * (Vector Alpha,double x) { return Vector(Alpha.x * x,Alpha.y * x);}

Vector operator / (Vector Alpha,double x) { return Vector(Alpha.x / x,Alpha.y / x);}

double sqr(double x) { return x * x;}

double dis(Point Alpha,Point Beta) { return sqrt(sqr(Alpha.x - Beta.x) + sqr(Alpha.y - Beta.y));}

bool cmp(const Point &x,const Point &y) { if(x.x < y.x || x.x == y.x && x.y < y.y) return true;else return false;}

bool check(Point Alpha,Point Beta,Point Gama)
{
	Vector u = Beta - Alpha,v = Gama - Beta;
	if(u.x * v.y - v.x * u.y < 0) return true;else return false;
}

double Cross(Vector Alpha,Vector Beta) { return Alpha.x * Beta.y - Alpha.y * Beta.x;}

double Area(Point Alpha,Point Beta,Point Gama)
{
	return (Cross(Beta - Alpha,Gama - Alpha) / 2);
}

inline void Scan1(int N)
{
	top1 = top1 + 1;
	stk1[top1] = top1;
	top1 = top1 + 1;
	stk1[top1] = top1;
	for(int i = 3;i <= N;i++)
	{
		top1 = top1 + 1;
		stk1[top1] = i;
		while(check(point[stk1[top1 - 2]],point[stk1[top1 - 1]],point[stk1[top1]]) == false && top1 > 2) 
		{
			stk1[top1 - 1] = stk1[top1];
			top1 = top1 - 1;
	    }
	}
}

inline void Scan2(int N)
{
	top2 = top2 + 1;
	stk2[top2] = N;
	top2 = top2 + 1;
	stk2[top2] = N - 1;
	for(int i = N - 2;i >= 1;i--)
	{
		top2 = top2 + 1;
		stk2[top2] = i;
		while(check(point[stk2[top2 - 2]],point[stk2[top2 - 1]],point[stk2[top2]]) == false && top2 > 2) 
		{
			stk2[top2 - 1] = stk2[top2];
			top2 = top2 - 1;
	    }
	}
}

int main()
{
	read(N);
	for(int i = 1;i <= N;i++)
	{
		scanf("%lf%lf",&x,&y);
		point[i].x = x,point[i].y = y;
	}
	sort(point + 1,point + N + 1,cmp);
	memset(stk1,0,sizeof(stk1));
	top1 = 0;
    Scan1(N);
	memset(stk2,0,sizeof(stk2));
	top2 = 0;
	Scan2(N);
	for(int i = 1;i <= top1;i++)
	{
		top = top + 1;
		stk[top] = stk1[i];
	}
	for(int i = 2;i <= top2;i++)
	{
		top = top + 1;
		stk[top] = stk2[i];
	}
	double ans = 0;
	stk[top + 1] = stk[1],num = 3;
	for(int i = 1;i <= top;i++)
	{
		ans = max(ans,dis(point[stk[i]],point[stk[i + 1]]));
		while(Area(point[stk[i]],point[stk[i + 1]],point[stk[num]]) 
		    < Area(point[stk[i]],point[stk[i + 1]],point[stk[num + 1]]))
		    {
		    	num++;
		    	if(num == top + 1) num = 1;
			}
		ans = max(ans,max(dis(point[stk[i]],point[stk[num]]),dis(point[stk[i + 1]],point[stk[num]])));
	}
	printf("%.3lf\n",ans);
	return 0;
}

   👆上述就是我们利用旋转卡壳算法求出二维凸包的直径~，那么关于旋转卡壳算法如此巧妙，怎会只有这一种用途~  ，旋转卡壳算法其实还可以用于解决大量的多边形的问题，而非仅仅局限于原来了解的基于凸包的一些具体问题，十分具有研究价值。因此我们，进行一定的拓展思考可以发现旋转卡壳还能做这些事情~😄：

    2.旋转卡壳——凸多边形的宽度：

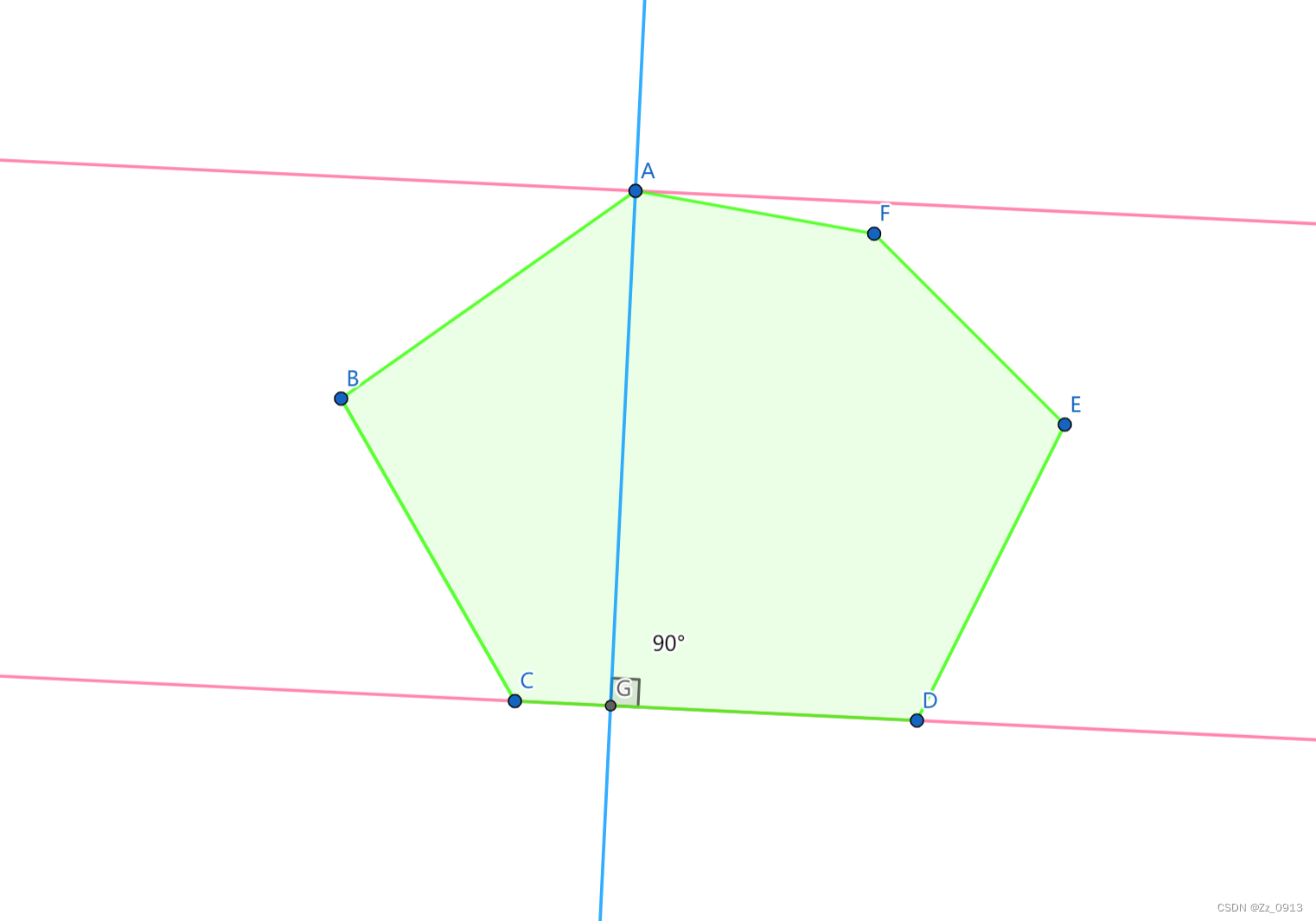
      👆 在矩形的定义中，宽是指短边，则在凸多边形的宽中，按照旋转卡壳的性质，就是这个对踵点到对应边的最小距离（这个应该非常好理解）步骤也是非常简单：

  3.旋转卡壳——凸多边形之间的最小距离和最大距离：

       两个凸多边形P和Q之间的最小距离由多边形间的对踵点对确立。 存在凸多边形间的三种多边形间的对踵点对， 因此就有三种可能存在的最小距离模式：

      1.“顶点” —— “顶点”；

      2.“顶点” —— “边”；

      3.“边” —— “边”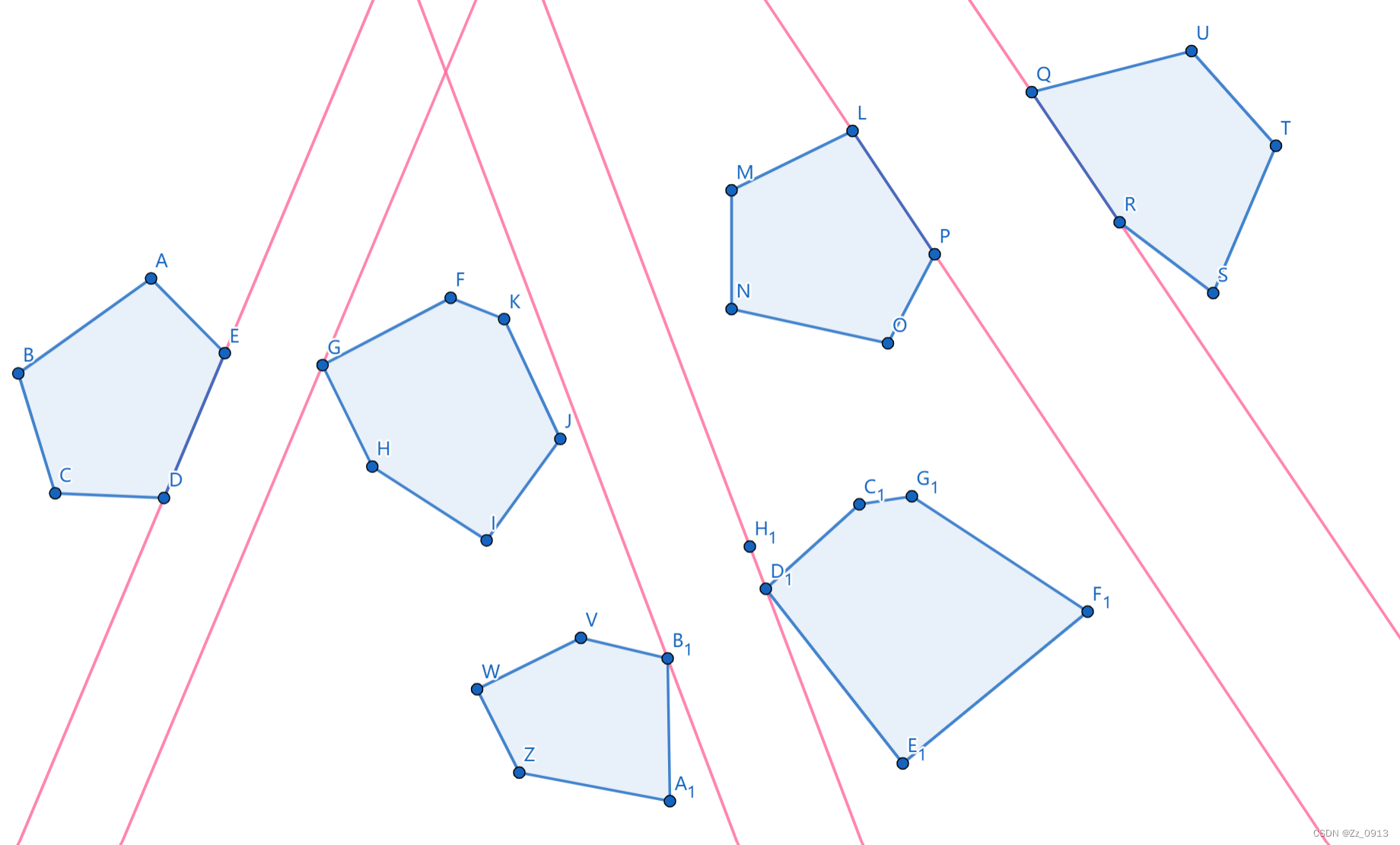

那么我们求解凸多边形之间的最小距离的算法步骤如下：

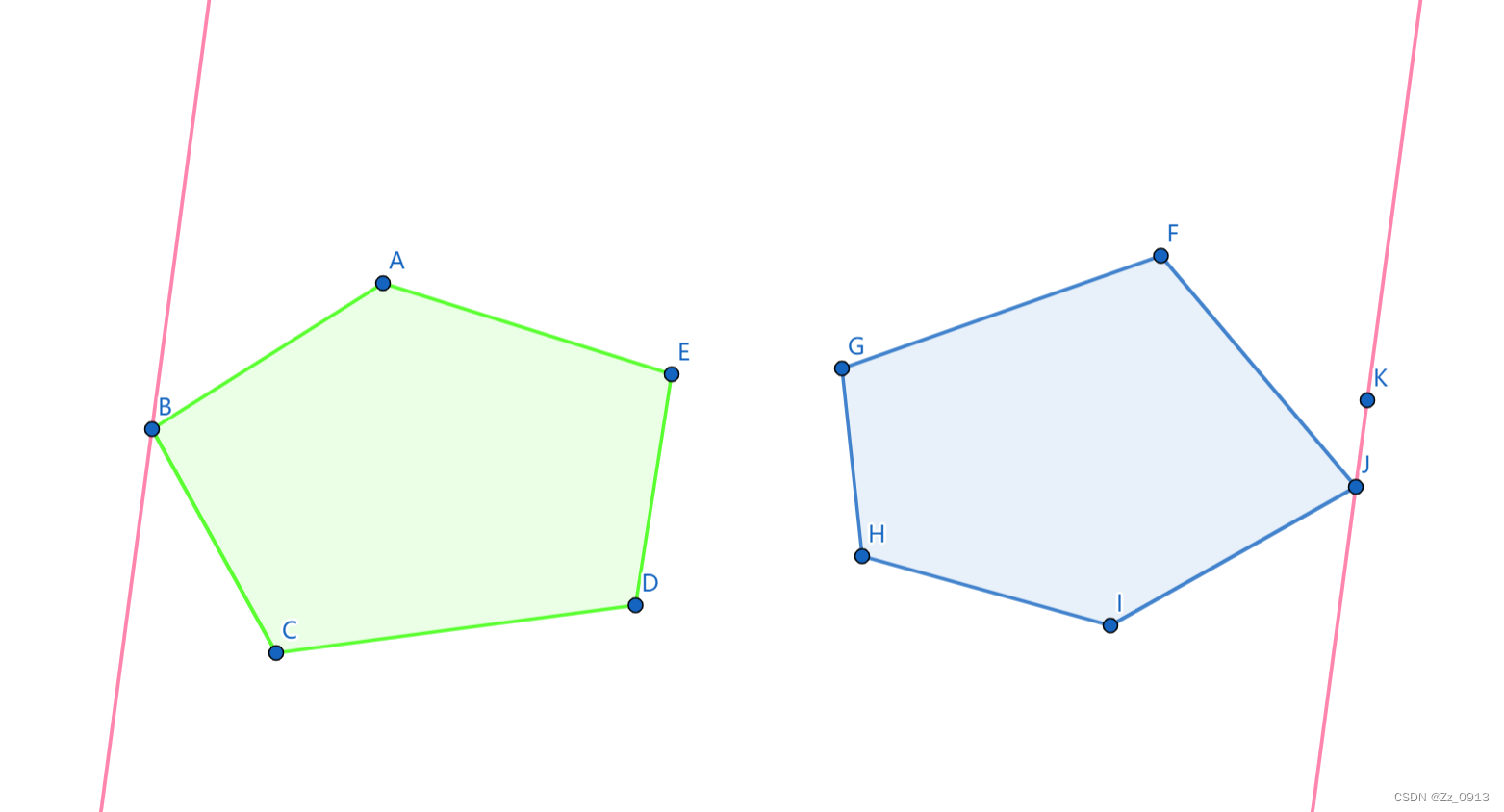
👆：凸多边形间的最大距离😄

        那么对于旋转卡壳我们可以看见这种算法对于凸多边形问题的解决能力很强，那么旋转卡壳还有很多用处，我们在下一篇文章--->《计算几何系列 —— 美妙的旋转卡壳算法~下》中作详细讲解，可能难度会有所提升，总之非常的巧妙~[doge]