第一章线性回归

最新推荐文章于 2024-09-12 13:19:42 发布

zz_wen

最新推荐文章于 2024-09-12 13:19:42 发布

阅读量577

点赞数 30

分类专栏：机器学习文章标签：线性回归算法回归

本文链接：https://blog.csdn.net/zz_wen/article/details/140992942

版权

机器学习专栏收录该内容

9 篇文章 0 订阅

订阅专栏

做题

例1

某银行需要根据客户薪资情况做贷款额度处理，现有方程如下：
$y = a x + b$ ,已知客户1，月薪10000，额度为25000，
客户2，月薪3000，额度为11000，
求月薪30000，额度为多少？
$10000 a + b = 250000$
$3000 a + b = 110000$
得 a = 2，b = 5000 $y = 2 x + 5000$
所以月薪 30000, 额度为65000

a 斜率
b 截距
x 自变量
y 因变量

例2

某银行需要根据客户薪资情况做贷款额度处理，现有方程如下：
$y = ax_1 + bx_2 + c$ ,
已知客户1，月薪10000，有房子，额度为35000，
客户2，月薪3000，有房子，额度为21000，
客户3，月薪15000，无房子，额度为35000，
求月薪30000，有房子，额度为多少？

$10000 a + 1 b + c = 350000$
$3000 a + 1 b + c = 210000$
$15000 a + 0 b + c = 350000$
得 a = 2，b = 10000, c = 50000
$y=2x_1 + 10000x_2 + 5000$

所以月薪 30000, 有房子, 额度为75000
a b 斜率
c 截距
x 自变量
y 因变量

总结：
根据一些已知点，求出方程，然后求出需要预测的值

基本概念

自变量和因变量之间的线性关系
x 自变量
y 因变量
方程线性关系

方程

$y = w_0 + w_1 * x_1 + w_2 * x_2 + .... + w_n * x_n$

参数
- 斜率 (权重)： w1,w2,…,wn
- 截距 (偏置)： w0
- 目标（输出变量）： y
- 输入变量： x

说明

数学上往往是比较精准的值，而实际生活中，不会有精准值，往往都是预估值（估计，感觉，大概）
以此引申出机器学习，根据一些数据，得到一个方程，因而预测未来的值
举例
$y = 2 x + 5$

x	y	y真实值
1	7	8
2	9	9
3	11	10

这就是回归问题

线性回归模型

定义： 线性回归模型是一种回归模型，它假设输入变量和输出变量之间存在线性关系。线性回归模型试图找到一条直线，使得这条直线尽可能地接近数据点，从而最小化模型预测值与真实值之间的差异。
**公式: ** $y=w_0+w_1∗x_1+w_2∗x_2+...+w_n∗x_n$
参数
- **斜率 (权重)：**w1,w2,…,wn表示特征与目标变量之间的关系强度和方向
- **截距 (偏置)：**w0表示在没有特征输入时目标变量的预测值
- 目标（输出变量）： y 表示要预测的目标值。

损失函数

损失函数是机器学习中用来衡量模型预测值与真实值之间差异的一个函数。损失函数的值越小，表示模型的预测值与真实值越接近，模型的性能越好。在回归问题中，常用的损失函数是均方误差（MSE, Mean Squared Error）。

均方误差

定义：模型预测值与真实值之差的平方的均值
公式： $MSE=1/n∑(y_i−ŷ_i)^2$ ，其中 $y_i$ 是真实值， $ŷ_i$ 是预测值

$1/6\sum_{i=1}^{6} (26 - 24.66666667)^2 + (30 - 32.26666667)^2 + (38- 39.86666667)^2 + (50- 47.46666667)^2 + (58- 55.06666667)^2 + (60- 62.66666667)^2 = 5.42$

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from matplotlib import rcParams

# 设置matplotlib的字体
rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体为黑体
rcParams['axes.unicode_minus'] = False  # 正确显示负号

# 简单线性回归
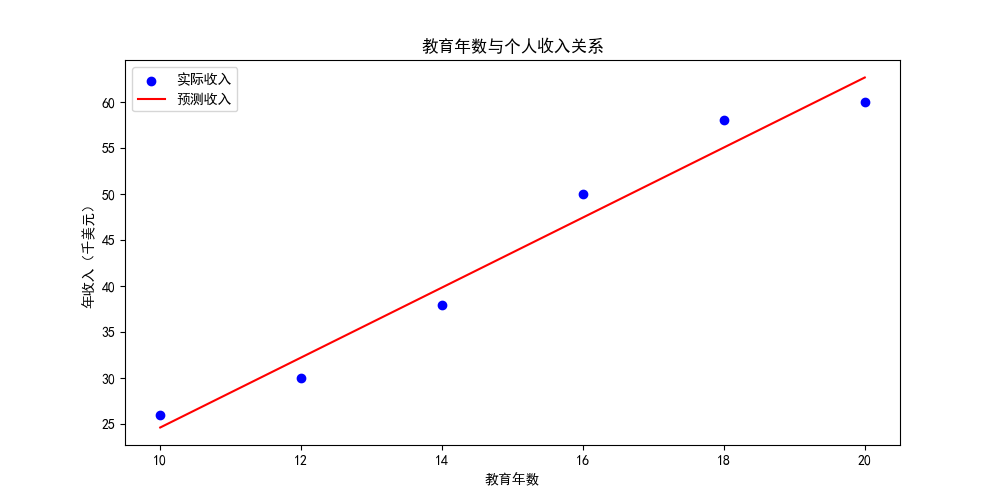
education_years = np.array([10, 12, 14, 16, 18, 20])  # 教育年数
income = np.array([26, 30, 38, 50, 58, 60])  # 个人年收入（以千美元计）

simple_model = LinearRegression()
simple_model.fit(education_years.reshape(-1, 1), income)

# 预测
income_pred = simple_model.predict(education_years.reshape(-1, 1))
print(income_pred)
# 计算评估指标
simple_mse = mean_squared_error(income, income_pred)

# 绘制结果
plt.figure(figsize=(10, 5))
plt.scatter(education_years, income, color='blue', label='实际收入')
plt.plot(education_years, income_pred, color='red', label='预测收入')
plt.title('教育年数与个人收入关系')
plt.xlabel('教育年数')
plt.ylabel('年收入（千美元）')
plt.legend()
plt.show()

print(f"简单线性回归评估指标:\n均方误差(MSE): {simple_mse:.2f}")

# 分析结果
analysis_text = print(f"""
简单线性回归结果分析：
每增加一年的教育，预期收入增加约 {simple_model.coef_[0]:.2f} 千美元。
""")

那么有误差，应该如何优化呢？

损失函数的优化

目的：把损失函数降得越低越好

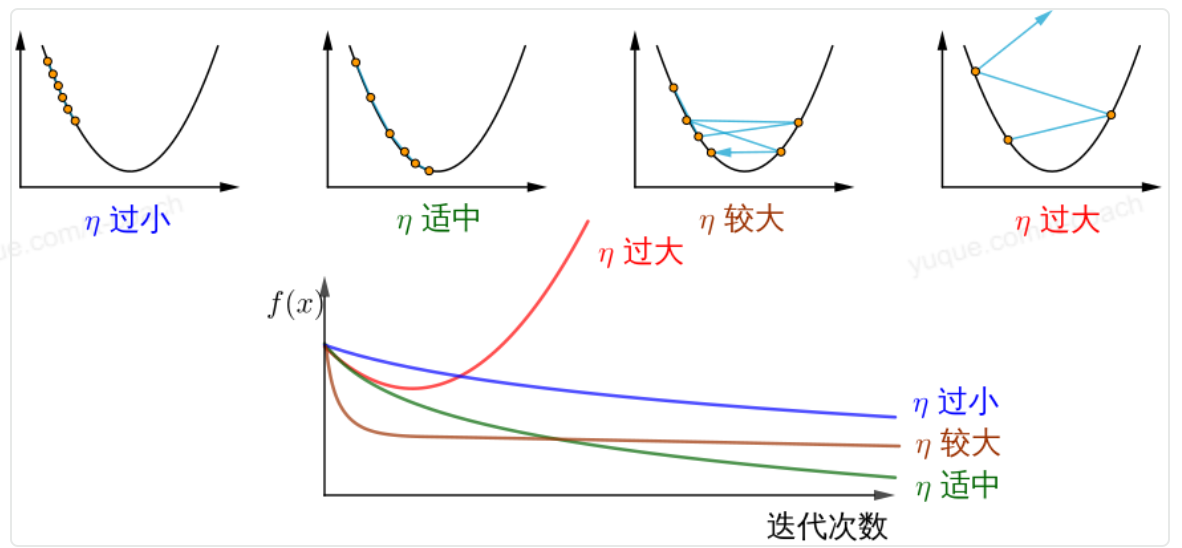
梯度下降

想象一下你站在一个不规则的山谷中，你的目标是找到山谷的最低点。但是，你无法看到整个山谷的全貌，只能感知自己所处位置的地形情况。梯度下降就像是你在这样的情况下尝试下山的过程。

初始化位置：开始时，你随机选择一个位置作为起始点，这对应于梯度下降中模型参数的初始值。
查看斜率：你观察脚下的斜率（即梯度），斜率指向的是坡度最陡的方向。在数学上，梯度是一个向量，它指出了函数增长最快的方向，因此负梯度则指向了函数减少最快的方向。
向下走一小步：根据斜率的方向，你朝着斜率的反方向迈出一步，因为你的目标是下山而不是上山。这一步的大小称为“学习率”，它决定了你每次更新参数时移动的距离。
重复步骤：到达新的位置后，你再次观察斜率，并继续朝着斜率的反方向移动。这个过程会一直重复，直到你达到一个足够平坦的地方，或者达到了预定的停止条件。
停止条件：当你发现周围的地形变得平坦，即梯度接近于零时，或者已经达到了预设的迭代次数，你就认为找到了一个局部最小值或足够接近全局最小值的位置，并停止移动。

这就是梯度下降的基本思想。在机器学习中，我们使用这种方法来逐步调整模型参数，以最小化训练数据上的预测误差。

数学公式
$θ_{n+1}=θ_n−η⋅∇J(θ)$

$θ_{n+1}$ ：下一个值
$θ_n$ ：当前值（当前网络参数值）
−：减号，梯度的反向（梯度的反方向为函数值下降最快的方向）
η：学习率或步长，控制每一步走的距离；不要太快以免错过了最佳景点，不要太慢以免时间太长（需要手动调整的超参数）
∇：梯度，表示函数当前位置的最快上升点（梯度向量指向上坡，负梯度向量指向下坡）
J(θ)：函数（等待优化的目标函数）

例子
$J(x,y)=x^2 + 2y^2$
计算函数梯度
$\frac{\partial J(x,y)}{\partial x} = 2x$
$\frac{\partial J(x,y)}{\partial y} = 4y$
设初始点为 $x_0,y_0)=(−3,−3)$ ，学习率 η=0.1，根据梯度下降公式可得参数迭代过程的计算公式：
$(x_{n+1},y_{n+1}) = (x_{n},y_{n}) - \eta \cdot \nabla J(x,y) = (x_{n},y_{n}) - \eta \cdot (2x,4y)$

计算下一个点
$x_1,y_1) = (-3,-3) - 0.1 * (2 * - 3,4 * - 3) = (−3+0.6,−3+1.2)=(−2.4,−1.8)$
终止条件为 J(x,y)<0.005

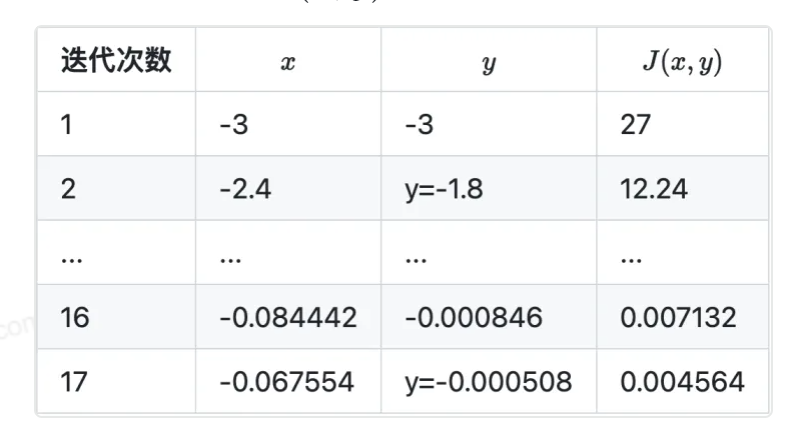
迭代 17 次后，J(x,y)=0.004564，满足小于 0.005 的条件，停止迭代。

小批量梯度下降 (Mini-Batch Gradient Descent)：使用数据集的一部分进行参数更新
随机梯度下降 (Stochastic Gradient Descent)：使用单个数据点进行参数更新
正规方程法：使用矩阵运算直接求解最优参数

# 导入必要的库，用于数据处理和可视化
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 导入自定义的线性回归类
from linear_regression import LinearRegression

# 读取世界幸福报告的数据集
data = pd.read_csv('../data/world-happiness-report-2017.csv')

# 将数据集分为训练集和测试集
# 得到训练和测试数据
train_data = data.sample(frac=0.8)
test_data = data.drop(train_data.index)

# 定义输入和输出参数的列名
input_param_name = 'Economy..GDP.per.Capita.'
output_param_name = 'Happiness.Score'

# 提取训练集和测试集的输入和输出参数
x_train = train_data[[input_param_name]].values
y_train = train_data[[output_param_name]].values

x_test = test_data[input_param_name].values
y_test = test_data[output_param_name].values

# 绘制训练集和测试集的数据点
plt.scatter(x_train, y_train, label='Train data')
plt.scatter(x_test, y_test, label='test data')
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title('Happy')
plt.legend()
plt.show()

# 定义梯度下降的迭代次数和学习率
num_iterations = 500
learning_rate = 0.01

# 初始化线性回归模型
linear_regression = LinearRegression(x_train, y_train)
# 训练模型并获取成本历史记录
(theta, cost_history) = linear_regression.train(learning_rate, num_iterations)

# 打印训练前后的成本
print('开始时的损失：', cost_history[0])
print('训练后的损失：', cost_history[-1])

# 绘制成本随迭代次数变化的曲线
plt.plot(range(num_iterations), cost_history)
plt.xlabel('Iter')
plt.ylabel('cost')
plt.title('GD')
plt.show()

# 预测新的数据点
predictions_num = 100
x_predictions = np.linspace(x_train.min(), x_train.max(), predictions_num).reshape(predictions_num, 1)
y_predictions = linear_regression.predict(x_predictions)

# 绘制训练集、测试集和预测结果的数据点
plt.scatter(x_train, y_train, label='Train data')
plt.scatter(x_test, y_test, label='test data')
plt.plot(x_predictions, y_predictions, 'r', label='Prediction')
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title('Happy')
plt.legend()
plt.show()