LCP

定义

LCP，最长公共前缀（并不是LCS最长公共子序列），这货其实一般是对于一个字符串的后缀而言的。

基于后缀数组的LCP

思想

因为和后缀有关，所以在后缀数组的基础上实现。

实现

定义H[i]表示SA[i-1]和SA[i]的最长公共前缀，rank[i]表示i的名次，那么不难发现SA[i]和SA[j]（i＜j）的最长公共前缀就是H[i+1]，H[i+2],H[i+3],……,H[j]中的最小值，也就是RMQ问题！RMQ问题我们有办法快速求得，现在唯一的问题就是这个H数组怎么构造。

O(n^2)的算法很容易想到，但是立刻让之前辛辛苦苦的倍增算法白费了。所以我们需要另想办法，先用aaaabbaaab举个例子：

1  aaaabbaaab
7  aaab         H[2]=3 h[7]=3
2  aaabbaaab    H[3]=3 h[2]=3
8  aab          H[4]=2 h[8]=2
3  aabbaaab     H[5]=3 h[3]=3
9  ab           H[6]=1 h[9]=1
4  abbaaab      H[7]=2 h[4]=2
10 b            H[8]=0 h[10]=0
6  baaab        H[9]=1 h[6]=1
5  bbaaab       H[10]=1 h[5]=1

求7(SA[2])和9(SA[6])的公共前缀，那么就是min(3,2,3,1)=1。

设h[i]=H[rank[i]]，我们发现，h[i]>=h[i-1]-1！这难道是巧合吗？不是的，我们可以证明得到：（k是SA[rank[i-1]-1]，也就是排序过后i-1的前一个）

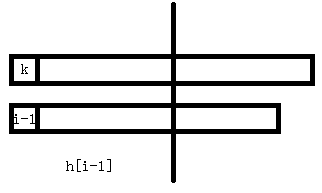
①当h[i-1]>1时
因为h[i-1]>1，说明至少有2个匹配到了。我们现在把第一个删除，就可以得到后缀k+1和i，那么后缀k+1肯定在i前面。显然SA[rank[k+1]]_{SA[rank[i]]之间所有的后缀的前h[i-1]-1位是和k+1和i一样的（想一想，为什么）。又因为SA[rank[k+1]]}SA[rank[i]]的最长公共前缀是最小的h，所以每一个h都>=h[i-1]-1，由此得到h[i]>=h[i-1]-1。

下面给出示意图：

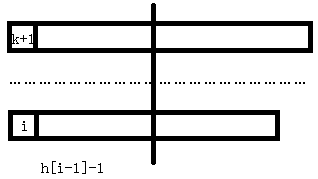
②当h[i-1]<=1时
之前k+1一定在i前面，而当h[i-1]<=1时，k+1就不一定在i前面了（因为把LCP删光了）。这种情况怎么办？我们换一种思路证明：因为h[i-1]<=1，所以h[i-1]-1<=0。又因为h[i]>=0，所以h[i]>=h[i-1]-1。

既然知道了这个性质，那么我们就算h，然后把h送给对应的H，这样就可以把H数组构造完成了。至于RMQ问题，就不需要多说了。

模板

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxl=200000,maxt=18;

int len,SA[maxl+5],rk[maxl+5],t[maxl+5],ha[maxl+5],H[maxl+5],RMQ[maxl+5][maxt+5];
char now[maxl+5];

void make_SA(char* s)
{
	int MAX=0;len=strlen(s+1);
	memset(ha,0,sizeof(ha));
	for (int i=1;i<=len;i++) {ha[rk[i]=s[i]]++;if (rk[i]>MAX) MAX=rk[i];}
	for (int i=1;i<=MAX;i++) ha[i]+=ha[i-1];
	for (int i=len;i>=1;i--) SA[ha[rk[i]]--]=i;
	for (int k=1;k<=len;k<<=1)
	{
		int p=0;
		for (int i=len-k+1;i<=len;i++) t[++p]=i;
		for (int i=1;i<=len;i++) if (SA[i]>k) t[++p]=SA[i]-k;
		memset(ha,0,sizeof(ha));
		for (int i=1;i<=len;i++) ha[rk[t[i]]]++;
		for (int i=1;i<=MAX;i++) ha[i]+=ha[i-1];
		for (int i=len;i>=1;i--) SA[ha[rk[t[i]]]--]=t[i];
		memcpy(t,rk,sizeof(t));
		p=1;rk[SA[1]]=1;
		for (int i=2;i<=len;i++)
			if (t[SA[i-1]]==t[SA[i]]&&t[SA[i-1]+k]==t[SA[i]+k]) rk[SA[i]]=p; else rk[SA[i]]=++p;
		if (p==len) break;
		MAX=p;
	}
}
void make_H() //处理H数组
{
	int k=0;
	for (int i=1;i<=len;i++)
	{
		if (k) k--;int j=SA[rk[i]-1];if (j==0) continue;
		while (now[i+k]==now[j+k]) k++;
		RMQ[rk[i]][0]=H[rk[i]]=k;
	}
	int ln=log2(len); //RMQ
	for (int j=1;j<=ln;j++)
	for (int i=1;i<=len-(1<<j)+1;i++)
		RMQ[i][j]=min(RMQ[i][j-1],RMQ[i+(1<<j-1)][j-1]);
}
int LCP(int x,int y) //求后缀x和后缀y的LCP
{
	x=rk[x];y=rk[y];if (x>y) swap(x,y);x++;int j=log2(y-x+1);
	return min(RMQ[x][j],RMQ[y-(1<<j)+1][j]);
}
bool Eoln(char ch) {return ch==10||ch==13||ch==EOF;}
int reads(char* s)
{
	int len=0;
	char ch=getchar();if (ch==EOF) return 2;
	s[++len]=ch;while (!Eoln(s[len])) s[++len]=getchar();s[len--]=0;
	return 0;
}
void writei(int x,bool fl=false)
{
	if (x==0) {if (fl==false) putchar('0');return;}
	writei(x/10,true);putchar(x%10+48);
}
int main()
{
	freopen("LCP.in","r",stdin);
	freopen("LCP.out","w",stdout);
	reads(now);make_SA(now);make_H();
	return 0;
}

基于哈希的LCP

ps：学习刘汝佳大神(Orz,%%%)蓝书上LCP之后写的

思想

如何快速比较字符串？有一种方法是Hash，所以求LCP时的验证可以用Hash实现。
ps：当然，Hash有风险，可能会判断错误，不过错误概率比较小。如果一些LCP问题能用稳定方法（如后缀数组）解决，就尽量不要用基于哈希的LCP。

实现

比如这样的一个字符串（len为5），我们构造一个H(i)表示i~len哈希值：
abcde (ASCII码为97 98 99 100 101)

H(5)=101
H(4)=H(5)*Base+100=101*Base+100
H(3)=H(4)*Base+99=101*Base^2+100*Base+99
H(2)=H(3)*Base+98=101*Base^3+100*Base^2+99*Base+98
H(1)=H(2)*Base+97=101*Base^4+100*Base^2+99*Base^2+98*Base+97

（毕竟是哈希……Base乱取即可）
有一个问题就是素数怎么取比较好？刘汝佳大神表示可以放在unsigned long long里让H自然溢出，就不需要特别选个素数了。

定义Hash(i,len)为从i位开始，向右推len位（包括i）的哈希值，不难发现：
$Hash(i,len)=H(i)-H(i+len)\ast x^{len}$

预处理H(i)和x^len之后就可以很快求出Hash值。求i和j的LCP，只需要二分枚举长度len，判断Hash(i,len)是否和Hash(j,len)相同就行了。