极坐标系
在数学中,极坐标系是一个二维坐标系统。该坐标系统中的点由一个夹角和一段相对中心点——极点(相当于我们较为熟知的直角坐标系中的原点)的距离来表示。极坐标系的应用领域十分广泛,包括数学、物理、工程、航海以及机器人领域。在两点间的关系用夹角和距离很容易表示时,极坐标系便显得尤为有用;而在平面直角坐标系中,这样的关系就只能使用三角函数来表示。对于很多类型的曲线,极坐标方程是最简单的表达形式,甚至对于某些曲线来说,只有极坐标方程能够表示。
目录[隐藏] |
[编辑] 历史
众所周知,希腊人最早使用了角度和弧度的概念。天文学家喜帕恰斯(190-120 BC)制成了一张求各角所对弦的弦长函数的表格。并且,曾有人引用了他的极坐标系来确定恒星位置。在螺线方面,阿基米德描述了他的著名的螺线,一个半径随角度变化的方程。希腊人作出了贡献,尽管最终并没有建立整个坐标系统。
关于是谁首次将极坐标系应用为一个正式的坐标系统,流传着有多种观点。关于这一问题的较详尽历史,哈佛大学教授朱利安·科利奇(Julian Coolidge)的《极坐标系起源》[1][2]作了阐述。格雷瓜·德·圣-万桑特 (Grégoire de Saint-Vincent)和博纳文图拉·卡瓦列里,被认为在几乎同时、并独立地各自引入了极坐标系这一概念。圣-万桑特在1625年的私人文稿中进行了论述并发表于1647年,而卡瓦列里在1635进行了发表,而后又于1653年进行了更正。卡瓦列里首次利用极坐标系来解决一个关于阿基米德螺线内的面积问题。布莱士·帕斯卡随后使用极坐标系来计算抛物线的长度。
在1671年写成,1736年出版的《流数术和无穷级数》(Method of Fluxions)一书中,艾萨克·牛顿第一个将极坐标系应用于表示平面上的任何一点。牛顿在书中验证了极坐标和其他九种坐标系的转换关系。在1691年出版的《博学通报》(Acta eruditorum)(Acta eruditorum)一书中雅各布·伯努利正式使用定点和从定点引出的一条射线,定点称为极点,射线称为极轴。平面内任何一点的坐标都通过该点与定点的距离和与极轴的夹角来表示。伯努利通过极坐标系对曲线的曲率半径进行了研究。
实际上应用“极坐标”(polar coordinate system)这个术语的是由格雷古廖·丰塔纳(Gregorio Fontana)开始的,并且被18世纪的意大利数学家所使用。该术语是由乔治·皮科克(George Peacock)在1816年翻译席维斯·拉克鲁克斯(Sylvestre François Lacroix)的《微分学与积分学》(Traité du calcul différentiel et du calcul intégral)[3][4][5] 一书时,被翻译为英语的。
亚历克西斯·克莱罗和莱昂哈德·欧拉被认为是将平面极坐标系扩展到三维空间的数学家。
[编辑] 在极坐标系中表示点
正如所有的二维坐标系,极坐标系也有两个坐标轴: (半径坐标)和
(半径坐标)和 (角坐标、极角或方位角,有时也表示为
(角坐标、极角或方位角,有时也表示为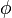 或
或 )。
)。 坐标表示与极点的距离,
坐标表示与极点的距离, 坐标表示按逆时针方向坐标距离0°射线(有时也称作极轴)的角度,极轴就是在平面直角坐标系中的x轴正方向。[6]
坐标表示按逆时针方向坐标距离0°射线(有时也称作极轴)的角度,极轴就是在平面直角坐标系中的x轴正方向。[6]
比如,极坐标中的(3,60°)表示了一个距离极点3个单位长度、和极轴夹角为60°的点。(−3,240°) 和(3,60°)表示了同一点,因为该点的半径为在夹角射线反向延长线上距离极点3个单位长度的地方(240° − 180° = 60°)。
极坐标系中一个重要的特性是,平面直角坐标中的任意一点,可以在极坐标系中有无限种表达形式。通常来说,点(r, θ)可以任意表示为(r, θ ± n×360°)或(−r, θ ± (2n + 1)180°),这里n是任意整数。[7] 如果某一点的r坐标为0,那么无论θ取何值,该点的位置都落在了极点上。
[编辑] 使用弧度单位
极坐标系中的角度通常表示为角度或者弧度,使用公式2π rad = 360°.具体使用哪一种方式,基本都是由使用场合而定。航海方面经常使用角度来进行测量,而物理学的某些领域大量使用到了半径和圆周的比来作运算,所以物理方面更倾向使用弧度。[8]
[编辑] 极坐标系与平面直角坐标系之间的转换
从极坐标  和
和  可以计算出直角坐标:
可以计算出直角坐标:
从直角坐标  和
和  ,也可以计算出极坐标:
,也可以计算出极坐标:
或
这方程式给出  在值域
在值域 ![(-\pi, \pi]](http://upload.wikimedia.org/wikipedia/zh/math/f/c/f/fcfe3f8f790d9246dce2f4e70705730f.png) 的弧度。[9]改用角度单位,值域为
的弧度。[9]改用角度单位,值域为 ![(-180^{\circ},180^{\circ}]](http://upload.wikimedia.org/wikipedia/zh/math/9/9/6/996e4dd964abf71fe0e711e3d4b22732.png) 。这些方程式假定极点是直角坐标系的原点
。这些方程式假定极点是直角坐标系的原点  ,极轴为x-坐标轴,而y-坐标轴方向的弧度为
,极轴为x-坐标轴,而y-坐标轴方向的弧度为  ,角度为
,角度为  。
。
大多数常用编程语言会特别设定一个函数,专门从  和
和  坐标计算出正确的角坐标
坐标计算出正确的角坐标  。例如,在C语言里,这函数标记为
。例如,在C语言里,这函数标记为 atan2(y,x) ,在Common Lisp里,标记为 (atan y x) 。对于这两种案例,计算结果是在值域 ![(-\pi, \pi]](http://upload.wikimedia.org/wikipedia/zh/math/f/c/f/fcfe3f8f790d9246dce2f4e70705730f.png) 内的弧度。这
内的弧度。这  的数值是复函数辐角的主值(principal value),注意到当
的数值是复函数辐角的主值(principal value),注意到当  和
和  都等于零时,辐角没有定义值;对于这案例,为了方便起见,将辐角设定为零。
都等于零时,辐角没有定义值;对于这案例,为了方便起见,将辐角设定为零。
假若需要,将角坐标  在值域
在值域 ![(-\pi, \pi]](http://upload.wikimedia.org/wikipedia/zh/math/f/c/f/fcfe3f8f790d9246dce2f4e70705730f.png) 的数值加上
的数值加上  ,则可得到在值域
,则可得到在值域  的数值。
的数值。
[编辑] 极坐标方程
用极坐标系描述的曲线方程称作极坐标方程,通常表示为r为自变量θ的函数。
极坐标方程经常会表现出不同的对称形式,如果r(−θ) = r(θ),则曲线关于极点(0°/180°)对称,如果r(π−θ) = r(θ),则曲线关于极点(90°/270°)对称,如果r(θ−α) = r(θ),则曲线相当于从极点逆时针方向旋转α°。
[编辑] 圆
在极坐标系中,圆心在(r0, φ) 半径为 a 的圆的方程为
该方程可简化为不同的方法,以符合不同的特定情况,比如方程
表示一个以极点为中心半径为a的圆。[10]
[编辑] 直线
经过极点的射线由如下方程表示
-
 ,
,
其中φ为射线的倾斜角度,若 m为直角坐标系的射线的斜率,则有φ = arctan m。 任何不经过极点的直线都会与某条射线垂直。[11] 这些在点(r0, φ)处的直线与射线θ = φ 垂直,其方程为
-
 .
.
[编辑] 玫瑰线
极坐标的玫瑰线(polar rose)是数学曲线中非常著名的曲线,看上去像花瓣,它只能用极坐标方程来描述,方程如下:
-
 或者
或者
-

如果k是整数,当k是奇数时那么曲线将会是k个花瓣,当k是偶数时曲线将是2k个花瓣。如果k为非整数,将产生圆盘状图形,且花瓣数也为非整数。注意:该方程不可能产生4的倍数加2(如2,6,10……)个花瓣。变量a代表玫瑰线花瓣的长度。
[编辑] 阿基米德螺线
阿基米德螺线在极坐标里使用以下方程表示:
-
 .
.
改变参数a将改变螺线形状,b控制螺线间距离,通常其为常量。阿基米德螺线有两条螺线,一条θ > 0,另一条θ < 0。两条螺线在极点处平滑地连接。把其中一条翻转 90°/270°得到其镜像,就是另一条螺线。
[编辑] 圆锥曲线
圆锥曲线方程如下:
其中l表示半正焦弦,e表示离心率。 如果e < 1,曲线为椭圆,如果e = 1,曲线为抛物线,如果e > 1,则表示双曲线。
[编辑] 其他曲线
由于坐标系统是基于圆环的,所以许多有关曲线的方程,极坐标要比直角坐标系(笛卡尔形式)简单得多。比如伯努利双纽线, 蚶线(limaçon), 还有 心脏线。
[编辑] 复数
复数的通常矩形形式为a + bi,在极坐标中也可以表示为两种不同的方式:
 ,简写为
,简写为 

等同于欧拉公式。[12] 复数在直角坐标系和极坐标系的转换通过以下公式实现:
-

-
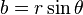
-
其中

复数的乘法、除法以及指数以及开方运算,在极坐标中会比在直角坐标中容易得多,他们分别是:
- 乘法:

- 除法:

- 指数(棣莫弗定理,De Moivre's formula):
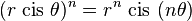
[编辑] 矢量微积分
微积分可适用于极坐标系下表达的等式。令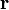 为位置矢量
为位置矢量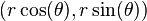 ,由 r 与随时间t变化的
,由 r 与随时间t变化的 表达,
表达, 是
是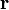 方向上的单位矢量,
方向上的单位矢量, 是以
是以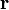 为起始顺时针旋转的角度单位矢量。第一和第二个位置的表达式是:
为起始顺时针旋转的角度单位矢量。第一和第二个位置的表达式是:
-
 .
.
-

令 为被一条连接焦点与曲线上一点的线所划分出的区域,则
为被一条连接焦点与曲线上一点的线所划分出的区域,则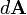 就是由
就是由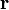 和
和 所构平行四边形区域的一半。
所构平行四边形区域的一半。
-
 ,
,
所以,整个区域就是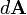 关于时间的积分。
关于时间的积分。
[编辑] 应用
[编辑] 行星运动的开普勒定律
极坐标提供了一个表达开普勒行星运行定律的自然数的方法。开普勒第一定律,认为环绕一颗恒星运行的行星轨道形成了一个椭圆,这个椭圆的一个焦点在质心上。上面所给出的二次曲线部分的等式可用于表达这个椭圆。 开普勒第二定律,即等域定律,认为连接行星和它所环绕的恒星的线在等时间间隔所划出的区域是面积相等的,即 是常量。这些等式可由牛顿运动定律推得。在开普勒行星运动定律中有相关运用极坐标的详细推导。
是常量。这些等式可由牛顿运动定律推得。在开普勒行星运动定律中有相关运用极坐标的详细推导。
[编辑] 三维空间
极坐标系可被扩展到三维空间中,形成圆柱坐标系和球形坐标系两个不同的坐标系。
[编辑] 圆柱坐标系
与将直角坐标系扩展为三维的方法相似,圆柱坐标系是在二维极坐标系的基础上增添了第三条用于测量高于平面的点的高度的坐标所构成的。这第三条坐标通常表示为h。所以圆柱坐标表示为(r, θ, h)。
通过以下公式,圆柱坐标可用直角坐标表达:
[编辑] 球坐标系
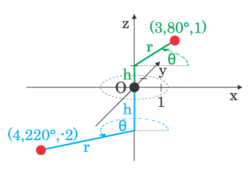
球坐标系也可以运用坐标(ρ, φ, θ)扩展为三维,其中ρ是距离球心的距离,φ是距离z轴的角度(称作余纬度或顶角,角度从0到180°),θ是距离x轴的角度(与极坐标中一样)。这个坐标系被称作球坐标系,与用于地球的经度和纬度相似,纬度就是余角φ,取决于δ=90°-φ,经度可通过l=θ-180°算得。[13]
通过以下公式,球坐标可用直角坐标表达:
-

-

-
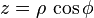
-
- 来源:http://zh.wikipedia.org/wiki/%E6%9E%81%E5%9D%90%E6%A0%87%E7%B3%BB












 的径向坐标为3、角坐标为60°,点
的径向坐标为3、角坐标为60°,点
 的径向坐标为4、角坐标为210°。
的径向坐标为4、角坐标为210°。





 (参阅
(参阅
 (
(


 的圆。
的圆。


























 4053
4053

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








