K-最近邻算法

最新推荐文章于 2025-10-06 15:14:38 发布

原创

最新推荐文章于 2025-10-06 15:14:38 发布 · 1.7w 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据

K-最近邻(KNN)是一种简单的分类算法，通过计算测试数据与训练集中每个数据的欧几里得距离，选择最近的K个邻居并根据它们的类别决定测试数据的分类。在实际应用中，需要注意训练集的公平性，算法优化以及大规模数据时的计算复杂度问题。在编码实现过程中，排序细节如数据类型的选择是常见难点。

介绍

KNN算法全名为k-Nearest Neighbor，就是K最近邻的意思。KNN也是一种分类算法。但是与之前说的决策树分类算法相比，这个算法算是最简单的一个了。算法的主要过程为：

1、给定一个训练集数据，每个训练集数据都是已经分好类的。
2、设定一个初始的测试数据a，计算a到训练集所有数据的欧几里得距离，并排序。

3、选出训练集中离a距离最近的K个训练集数据。

4、比较k个训练集数据，选出里面出现最多的分类类型，此分类类型即为最终测试数据a的分类。

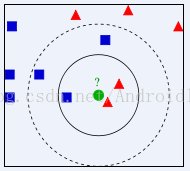
下面百度百科上的一张简图：

KNN算法实现

首先测试数据需要2块，1个是训练集数据，就是已经分好类的数据，比如上图中的非绿色的点。还有一个是测试数据，就是上面的绿点，当然这里的测试数据不会是一个，而是一组。这里的数据与数据之间的距离用数据的特征向量做计算，特征向量可以是多维度的。通过计算特征向量与特征向量之间的欧几里得距离来推算相似度。定义训练集数据trainInput.txt:

a 1 2 3 4 5 
b 5 4 3 2 1 
c 3 3 3 3 3 
d -3 -3 -3 -3 -3 
a 1 2 3 4 4 
b 4 4 3 2 1 
c 3 3 3 2 4 
d 0 0 1 1 -2

待测试数据testInput，只有特征向量值：

1 2 3 2 4 
2 3 4 2 1 
8 7 2 3 5 
-3 -2 2 4 0 
-4 -4 -4 -4 -4 
1 2 3 4 4 
4 4 3 2 1 
3 3 3 2 4 
0 0 1 1 -2

下面是主程序：

package DataMing_KNN;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Arrays;
import java.

最低0.47元/天解锁文章