梯度下降法（Gradient Descent）

概念

梯度下降法（通常也称为最速下降法）是一个一阶最优化算法。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值点，这个过程则被称为梯度上升法。

梯度下降方法基于以下的观察：如果实值函数 $\mathrm F(\mathbf x)$ 在点 $\mathbf a$ 处可微且有定义，那么函数 $\mathrm F(\mathbf x)$ 在 $\mathbf a$ 沿着梯度相反方向 $-\nabla \mathrm F(\mathbf a)$ 下降最快。

因此，如果 $\mathbf b=\mathbf a-\gamma \nabla \mathrm F(\mathbf a)$，对于 $\gamma>0$ 且为一个够小数值假设成立时，那么$\mathrm F(\mathbf a)>\mathrm F(\mathbf b)$ （因为 $-\nabla \mathrm F(\mathbf a)$ 为梯度反方向，沿着该方向递减，a到b是沿着梯度反方向）。考虑到这一点，可以从函数 $\mathrm F$ 的局部极小值的初始估计 $x_0$ 出发，并考虑如下序列$\mathbf x_0,\mathbf x_1,\mathbf x_2,...$ ，使得 $\mathbf x_{n+1}=\mathbf x_n-\gamma_n \nabla \mathrm F(\mathbf x_n) ，n \ge 0$ ，因此可得到 $\mathrm F(\mathbf x_0) \ge \mathrm F(\mathbf x_1) \ge \mathrm F(\mathbf x_2)...$，如果顺利的话序列 $(\mathbf x_n)$ 收敛到期望的极限。注意每次迭代的步长 $\gamma$ 可以改变。

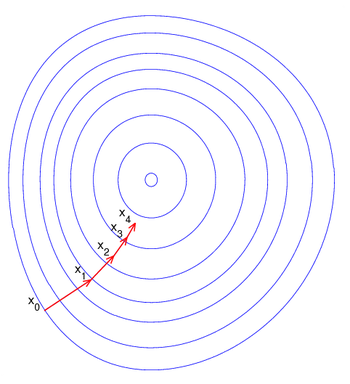
下图的图片示例了这一过程，这里假设 $\mathrm F$ 定义在平面上，并且函数图像是一个碗形。蓝色的曲线是等高线（水平集），即函数 $\mathrm F$ 为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线垂直）。沿着梯度下降方向，将最终到达碗底，即函数 $\mathrm F$ 值最小的点。

最速下降法是用负梯度方向为搜索方向的，最速下降法越接近目标值，步长越小，前进越慢。

梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。

步长的确定比较麻烦，太大了的话可能会发散，太小收敛速度又太慢。一般确定步长的方法是由线性搜索算法来确定，即把下一个点的坐标看做是 $\mathbf x_{n+1}$ 的函数，然后求满足 $\mathrm F(\mathbf x_{n+1})$ 的最小值的 即可。

---

举例

举例一：求函数 $\mathbf f(\mathbf x)=\mathbf x^2$ 的最小值。利用梯度下降的方法解题步骤如下：

1、求梯度， $\nabla=2\mathbf x$;

2、向梯度相反的方向移动 $\mathbf x$，如下$\mathbf x \leftarrow \mathbf x-\gamma \nabla$ ，其中 $\gamma$ 为步长。如果步长足够小，则可以保证每一次迭代都在减小，但可能导致收敛太慢，如果步长太大，则不能保证每一次迭代都减少，也不能保证收敛。

3、循环迭代步骤2，直到 $\mathbf x$ 的值变化到使得 $\mathbf f(\mathbf x)$ 在两次迭代之间的差值足够小，比如0.00000001，也就是说，直到两次迭代计算出来的 $\mathbf f(\mathbf x)$ 基本没有变化，则说明此时 $\mathbf f(\mathbf x)$ 已经达到局部最小值了。

4、此时，输出 $\mathbf x$ ，这个 $\mathbf x$ 就是使得函数 $\mathbf f(\mathbf x)$ 最小时的 $\mathbf x$ 的取值 。

---

举例二：梯度下降法处理一些复杂的非线性函数会出现问题，例如Rosenbrock函数 $\mathbf f(x,y)=(1-x)^2+100(y-x^2)^2$ .其最小值在 $(x,y)=(1,1)$ 处，数值为 $\mathbf f(x,y)=0$ 。但是此函数具有狭窄弯曲的山谷，最小值 $(x,y)=(1,1)$ 就在这些山谷之中，并且谷底很平。优化过程是之字形的向极小值点靠近，速度非常缓慢。

---

小结

梯度下降法其实是根据函数的梯度来确定函数的极小值 。最小二乘法也是找出误差最小的参数值，那二者的区别是什么呢？

相同：都是通过求导来求损失函数的最小值，在给定已知数据的前提下来进行参数估计，在已知数据中使估算值和实际值的总平方差尽量小（实际中不一定使用平方）。

不同：最小二乘法是直接对 $\Delta$ 求导找出全局最小，是非迭代法。而梯度下降法是一种迭代法，先给定一个 $\beta$，然后向 $\Delta$ 下降最快的方向调整 $\beta$ ，在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢，并且对初始点的选择极为敏感，其改进大多是在这两方面下功夫。