1.SVM对偶函数最后的优化问题



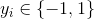
2. 对核函数进行缓存

由于该矩阵是对称矩阵,因此在内存中的占用空间可以为m(m+1)/2
映射关系为:

#define OFFSET(x, y) ((x) > (y) ? (((x)+1)*(x) >> 1) + (y) : (((y)+1)*(y) >> 1) + (x))
//...
for (unsigned i = 0; i < count; ++i)
for (unsigned j = 0; j <= i; ++j)
cache[OFFSET(i, j)] = y[i] * y[j] * kernel(x[i], x[j], DIMISION);
//...3. 求解梯度
既然α值是变量,因此对α值进行求导,后面根据梯度选取α值进行优化。
梯度:
for (unsigned i = 0; i < count; ++i) { gradient[i] = -1; for (unsigned j = 0; j < count; ++j) gradient[i] += cache[OFFSET(i, j)] * alpha[j]; }

若使W最大,则当α减少时,G越大越好。反之,G越小越好。
4. 序列最小化法(SMO)的约束条件
每次选取2个α值进行优化,其它α值视为常数,根据约束条件 得:
得:

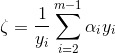

进行优化之后:

5. 制定选取规则
由于α的范围在区间[0,C],所以△α受α约束
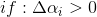
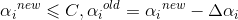




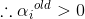

若选取的 和
和 异号,即λ=-1,则
异号,即λ=-1,则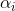 和
和 增减性相同
增减性相同
假设 ,
,
若 ,则
,则 ,此时应选取
,此时应选取
上述命题可化为(注: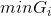 与
与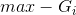 等价)
等价)


若选取的 和
和 同号,即λ=1,则
同号,即λ=1,则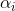 和
和 增减性相异
增减性相异
若 ,则
,则 ,此时应选取
,此时应选取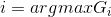 ,
,
上述命题可化为(注: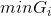 与
与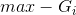 等价)
等价)


或

将上述结论进行整理,可得(为了简便此处只选取G前的符号与y的符号相异的情况)
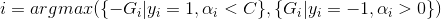
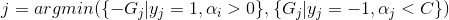
unsigned x0 = 0, x1 = 1;
//根据梯度选取进行优化的alpha值
{
double gmax = -DBL_MAX, gmin = DBL_MAX;
for (unsigned i = 0; i < count; ++i)
{
if ((alpha[i] < C && y[i] == POS || alpha[i] > 0 && y[i] == NEG) && -y[i] * gradient[i] > gmax)
{
gmax = -y[i] * gradient[i];
x0 = i;
}
else if ((alpha[i] < C && y[i] == NEG || alpha[i] > 0 && y[i] == POS) && -y[i] * gradient[i] < gmin)
{
gmin = -y[i] * gradient[i];
x1 = i;
}
}
}6. 开始进行求解
alpha要求在区间[0,C]内,对不符合条件的alpha值进行调整,调整规则如下。
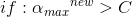
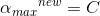

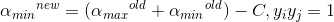

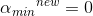

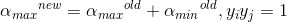
分2种情况,若λ=-1,即:
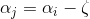
代入后得:

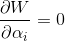
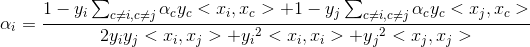
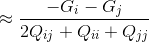
if (y[x0] != y[x1])
{
double coef = cache[OFFSET(x0, x0)] + cache[OFFSET(x1, x1)] + 2 * cache[OFFSET(x0, x1)];
if (coef <= 0) coef = DBL_MIN;
double delta = (- gradient[x0] - gradient[x1]) / coef;
double diff = alpha[x0] - alpha[x1];
alpha[x0] += delta;
alpha[x1] += delta;
unsigned max = x0, min = x1;
if (diff < 0)
{
max = x1;
min = x0;
diff = -diff;
}
if (alpha[max] > C)
{
alpha[max] = C;
alpha[min] = C - diff;
}
if (alpha[min] < 0)
{
alpha[min] = 0;
alpha[max] = diff;
}
}若λ=1,即:


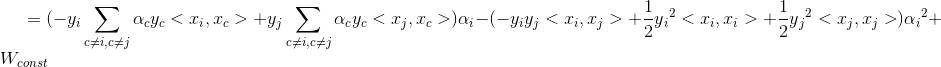
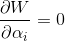


else
{
double coef = cache[OFFSET(x0, x0)] + cache[OFFSET(x1, x1)] - 2 * cache[OFFSET(x0, x1)];
if (coef <= 0) coef = DBL_MIN;
double delta = (-gradient[x0] + gradient[x1]) / coef;
double sum = alpha[x0] + alpha[x1];
alpha[x0] += delta;
alpha[x1] -= delta;
unsigned max = x0, min = x1;
if (alpha[x0] < alpha[x1])
{
max = x1;
min = x0;
}
if (alpha[max] > C)
{
alpha[max] = C;
alpha[min] = sum - C;
}
if (alpha[min] < 0)
{
alpha[min] = 0;
alpha[max] = sum;
}
}然后进行梯度调整,调整公式如下:
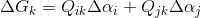
for (unsigned i = 0; i < count; ++i)
gradient[i] += cache[OFFSET(i, x0)] * delta0 + cache[OFFSET(i, x1)] * delta1;7.进行权重的计算
计算公式如下:


double maxneg = -DBL_MAX, minpos = DBL_MAX;
SVM *svm = &bundle->svm;
for (unsigned i = 0; i < count; ++i)
{
double wx = kernel(svm->weight, data[i], DIMISION);
if (y[i] == POS && minpos > wx)
minpos = wx;
else if (y[i] == NEG && maxneg < wx)
maxneg = wx;
}
svm->bias = -(minpos + maxneg) / 2;



 本文详细分析了支持向量机(SVM)的SMO算法,包括对偶函数的优化问题、核函数缓存、梯度求解、序列最小化法的约束条件以及优化规则。通过选取规则和权重计算,阐述了如何在[0,C]区间内调整α值,以实现SVM模型的优化。提供了代码地址供参考。"
130956343,6680800,RockyLinux9.2中部署k8s1.27+kubeadm+calico+BGP+OpenELB详细教程,"['kubernetes', '容器', '网络', '负载均衡']
本文详细分析了支持向量机(SVM)的SMO算法,包括对偶函数的优化问题、核函数缓存、梯度求解、序列最小化法的约束条件以及优化规则。通过选取规则和权重计算,阐述了如何在[0,C]区间内调整α值,以实现SVM模型的优化。提供了代码地址供参考。"
130956343,6680800,RockyLinux9.2中部署k8s1.27+kubeadm+calico+BGP+OpenELB详细教程,"['kubernetes', '容器', '网络', '负载均衡']
















 472
472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








