引言
面对这样的优化问题: min α 1 2 ∑ i = 1 m ∑ j = 1 m α ( i ) α ( j ) K ( x ( i ) ⋅ x ( j ) ) − ∑ i = 1 m α ( i ) s . t . ∑ i = 1 m α ( i ) y ( i ) = 0 , 0 ≤ α ( i ) ≤ C , i = 1 , 2 , ⋯ , m \begin{split} &\min_{\alpha}\;\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha^{(i)}\alpha^{(j)}K(x^{(i)}\cdot x^{(j)})-\sum_{i=1}^{m}\alpha^{(i)}\\ &s.t.\;\sum_{i=1}^{m}\alpha^{(i)}y^{(i)}=0\;,\;0\leq\alpha^{(i)}\leq C\;,\;i=1,2,\cdots,m \end{split} αmin21i=1∑mj=1∑mα(i)α(j)K(x(i)⋅x(j))−i=1∑mα(i)s.t.i=1∑mα(i)y(i)=0,0≤α(i)≤C,i=1,2,⋯,m
参数: α \alpha α是拉格朗日乘子构成的变量,有 α = ( α 1 , α 2 , ⋯ , α N ) T \alpha=(\alpha_1,\alpha_2,\cdots,\alpha_N)^T α=(α1,α2,⋯,αN)T,每一个拉格朗日乘子对应一个样本点,例如: α 1 → ( x 1 , y 1 ) \alpha_1\rightarrow (x_1,y_1) α1→(x1,y1)。
1.坐标下降法
每次只完成一个参数的更新。
我们接下来举一个简单的例子来说明:
arg
min
x
1
,
x
2
f
(
x
1
,
x
2
)
=
x
1
2
+
2
x
2
2
−
x
1
x
2
+
1
\arg\;\min_{x_1,x_2}f(x_1,x_2)=x_1^2+2x_2^2-x_1x_2+1
argx1,x2minf(x1,x2)=x12+2x22−x1x2+1
:初始值 ( x 1 ( 0 ) , x 2 ( 0 ) ) T (x_1^{(0)},x_2^{(0)})^T (x1(0),x2(0))T
:选择其中一个进行更新
例如选择
x
1
(
0
)
x_1^{(0)}
x1(0),固定
x
2
(
0
)
x_2^{(0)}
x2(0),使得问题转化为:
arg
min
x
1
,
x
2
f
(
x
1
,
x
2
(
0
)
)
\arg\;\min_{x_1,x_2}f(x_1,x_2^{(0)})
argx1,x2minf(x1,x2(0))
我们采用费马原理如下:
∂
f
∂
x
1
=
2
x
1
−
x
2
(
0
)
=
0
⇒
x
2
=
x
2
0
2
\frac{\partial f}{\partial x_1}=2x_1-x_2^{(0)}=0\Rightarrow x_2=\frac{x_2^{0}}{2}
∂x1∂f=2x1−x2(0)=0⇒x2=2x20
:更新 x 2 x_2 x2,固定 x 1 = x 1 1 x_1=x_1^{1} x1=x11,求解 x 2 x_2 x2
arg min x 1 , x 2 f ( x 1 ( 1 ) , x 2 ) \arg\;\min_{x_1,x_2}f(x_1^{(1)},x_2) argx1,x2minf(x1(1),x2)
∂ f ∂ x 2 = 4 x 2 − x 1 ( 1 ) ⇒ x 2 ( 1 ) = x 1 1 4 \frac{\partial f}{\partial x_2}=4x_2-x_1^{(1)}\Rightarrow x_2^{(1)}=\frac{x_1^{1}}{4} ∂x2∂f=4x2−x1(1)⇒x2(1)=4x11
:重复上面的 → \rightarrow →直到收敛为止。
坐标下降法可以应用在非线性支持向量机吗?
不妨选取 α 1 \alpha_1 α1,固定 α 2 , α 3 , ⋯ , α N \alpha_2,\alpha_3,\cdots,\alpha_N α2,α3,⋯,αN。
:初始值 α ( 0 ) = ( α 1 ( 0 ) , α 2 ( 0 ) , ⋯ , α N ( 0 ) ) \alpha^{(0)}=(\alpha_1^{(0)},\alpha_2^{(0)},\cdots,\alpha_N^{(0)}) α(0)=(α1(0),α2(0),⋯,αN(0))
:在固定 α 2 , α 3 , ⋯ , α N \alpha_2,\alpha_3,\cdots,\alpha_N α2,α3,⋯,αN下,求 α 1 \alpha_1 α1
使得: min α W ( α 1 , α 2 ( 0 ) , α 3 ( 0 ) , ⋯ , α N ( 0 ) ) s . t . α i y i = − ∑ i = 2 N α i ( 0 ) y i , 0 ≤ α i ≤ C \begin{split} &\min_{\alpha}\;W(\alpha_1,\alpha_2^{(0)},\alpha_3^{(0)},\cdots,\alpha_N^{(0)})\\ &s.t.\;\alpha_iy_i=-\sum_{i=2}^{N}\alpha_i^{(0)}y_i\;,\;0\leq \alpha_i\leq C \end{split} αminW(α1,α2(0),α3(0),⋯,αN(0))s.t.αiyi=−i=2∑Nαi(0)yi,0≤αi≤C
此时 α 1 \alpha_1 α1可以直接由约束条件得到具体的值,无法进行更新。
所以坐标下降法用于非线性支持向量机的方法失败了。
但是我们可以换个思路,固定剩余的 N − 2 N-2 N−2个变量,求两个变量,这就是接下来要讲的序列最小最优算法的最初想法。
2.SMO算法
SMO算法要解决如下问题: min α 1 2 ∑ i = 1 m ∑ j = 1 m α ( i ) α ( j ) K ( x ( i ) ⋅ x ( j ) ) − ∑ i = 1 m α ( i ) s.t. ∑ i = 1 m α ( i ) y ( i ) = 0 , 0 ≤ α ( i ) ≤ C , i = 1 , 2 , ⋯ , m \begin{split} &\min_{\alpha}\;\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha^{(i)}\alpha^{(j)}K(x^{(i)}\cdot x^{(j)})-\sum_{i=1}^{m}\alpha^{(i)}\\ &\textbf{s.t.}\;\sum_{i=1}^{m}\alpha^{(i)}y^{(i)}=0\;,\;0\leq\alpha^{(i)}\leq C\;,\;i=1,2,\cdots,m \end{split} αmin21i=1∑mj=1∑mα(i)α(j)K(x(i)⋅x(j))−i=1∑mα(i)s.t.i=1∑mα(i)y(i)=0,0≤α(i)≤C,i=1,2,⋯,m
我们选择两个变量,
α
1
,
α
2
\alpha_1\;,\;\alpha_2
α1,α2,其他变量固定,于是SMO的最优化问题的子问题为:
min
α
1
,
α
2
W
(
α
(
1
)
,
α
(
2
)
)
=
1
2
K
11
α
(
1
)
2
+
1
2
K
22
α
(
2
)
2
+
y
(
1
)
y
(
2
)
K
12
α
(
1
)
α
(
2
)
−
(
α
(
1
)
+
α
(
2
)
)
+
y
(
1
)
α
(
1
)
∑
i
=
3
m
y
(
i
)
α
(
i
)
K
i
1
+
y
(
2
)
α
(
2
)
∑
i
=
3
m
y
(
i
)
α
(
i
)
K
i
2
s.t.
α
(
1
)
y
(
1
)
+
α
(
2
)
y
(
2
)
=
−
∑
i
=
3
m
y
(
i
)
α
(
i
)
=
ζ
,
0
≤
α
(
i
)
≤
C
,
i
=
1
,
2
\begin{split} \min_{\alpha_1,\alpha_2}W(\alpha^{(1)},\alpha^{(2)})&=\frac{1}{2}K_{11}{\alpha^{(1)}}^2+\frac{1}{2}K_{22}{\alpha^{(2)}}^2+y^{(1)}y^{(2)}K_{12}\alpha^{(1)}\alpha^{(2)}\\ &-(\alpha^{(1)}+\alpha^{(2)})+y^{(1)}\alpha^{(1)}\sum_{i=3}^{m}y^{(i)}\alpha^{(i)}K_{i1}+y^{(2)}\alpha^{(2)}\sum_{i=3}^{m}y^{(i)}\alpha^{(i)}K_{i2}\\ \textbf{s.t.}\quad \quad \alpha^{(1)}y^{(1)}+&\alpha^{(2)}y^{(2)}=-\sum_{i=3}^{m}y^{(i)}\alpha^{(i)}=\zeta\;,\;0\leq\alpha^{(i)}\leq C\;,\;i=1,2 \end{split}
α1,α2minW(α(1),α(2))s.t.α(1)y(1)+=21K11α(1)2+21K22α(2)2+y(1)y(2)K12α(1)α(2)−(α(1)+α(2))+y(1)α(1)i=3∑my(i)α(i)Ki1+y(2)α(2)i=3∑my(i)α(i)Ki2α(2)y(2)=−i=3∑my(i)α(i)=ζ,0≤α(i)≤C,i=1,2
其中, K i j = K ( x i , x j ) , i , j = 1 , 2 , ⋯ , N K_{ij}=K(x_i,x_j)\;,\;i,j=1,2,\cdots,N Kij=K(xi,xj),i,j=1,2,⋯,N, ζ \zeta ζ是常数,目标函数中省略了不含 α ( 1 ) , α ( 2 ) \alpha^{(1)}\;,\;\alpha^{(2)} α(1),α(2)项。
为了叙述简单,记: g ( x ) = ∑ i = 1 m α ( i ) y ( i ) K ( x ( i ) , x ) + b E i = g ( x ( i ) ) − y ( i ) = ( ∑ j = 1 m α ( j ) y ( j ) K ( x ( j ) , x ( i ) ) + b ) − y ( i ) V i = ∑ j = 3 m α ( j ) y ( j ) K ( x ( j ) , x ( i ) ) = g ( x ( i ) ) − ∑ j = 1 2 α ( j ) y ( j ) K ( x ( j ) , x ( i ) ) − b \begin{split} &g(x)=\sum_{i=1}^{m}\alpha^{(i)}y^{(i)}K(x^{(i)},x)+b\\ &E_i=g(x^{(i)})-y^{(i)}=(\sum_{j=1}^{m}\alpha^{(j)}y^{(j)}K(x^{(j)},x^{(i)})+b)-y^{(i)}\\ &V_i=\sum_{j=3}^{m}\alpha^{(j)}y^{(j)}K(x^{(j)},x^{(i)})=g(x^{(i)})-\sum_{j=1}^2\alpha^{(j)}y^{(j)}K(x^{(j)},x^{(i)})-b \end{split} g(x)=i=1∑mα(i)y(i)K(x(i),x)+bEi=g(x(i))−y(i)=(j=1∑mα(j)y(j)K(x(j),x(i))+b)−y(i)Vi=j=3∑mα(j)y(j)K(x(j),x(i))=g(x(i))−j=1∑2α(j)y(j)K(x(j),x(i))−b
目标函数可写成:
W
(
α
(
1
)
,
α
(
2
)
)
=
1
2
K
11
α
(
1
)
2
+
1
2
K
22
α
(
2
)
2
+
y
(
1
)
y
(
2
)
K
12
α
(
1
)
α
(
2
)
−
(
α
(
1
)
+
α
(
2
)
)
+
y
(
1
)
α
(
1
)
v
1
+
y
(
2
)
α
(
2
)
v
2
W(\alpha^{(1)},\alpha^{(2)})=\frac{1}{2}K_{11}{\alpha^{(1)}}^{2}+\frac{1}{2}K_{22}{\alpha^{(2)}}^{2}+y^{(1)}y^{(2)}K_{12}\alpha^{(1)}\alpha^{(2)}-(\alpha^{(1)}+\alpha^{(2)})+y^{(1)}\alpha^{(1)}v_1+y^{(2)}\alpha^{(2)}v_2
W(α(1),α(2))=21K11α(1)2+21K22α(2)2+y(1)y(2)K12α(1)α(2)−(α(1)+α(2))+y(1)α(1)v1+y(2)α(2)v2
我们的表示方法如下: K 11 = K ( x 1 , x 2 ) , K 22 = K ( x 2 , x 2 ) K 12 = K ( x 1 , x 2 ) , K 1 j = K ( x 1 , x j ) K 2 j = K ( x 2 , x j ) \begin{split} &K_{11}=K(x_1,x_2)\;,\;K_{22}=K(x_2,x_2)\\ &K_{12}=K(x_1,x_2)\;,\;K_{1j}=K(x_1,x_j)\\ &K_{2j}=K(x_2,x_j) \end{split} K11=K(x1,x2),K22=K(x2,x2)K12=K(x1,x2),K1j=K(x1,xj)K2j=K(x2,xj)
由
α
(
1
)
y
(
1
)
=
ζ
−
α
(
2
)
y
(
2
)
\alpha^{(1)}y^{(1)}=\zeta-\alpha^{(2)}y^{(2)}
α(1)y(1)=ζ−α(2)y(2)可将
α
(
1
)
\alpha^{(1)}
α(1)表示为:
α
(
1
)
=
(
ζ
−
α
(
2
)
y
(
2
)
)
y
(
1
)
\alpha^{(1)}=(\zeta-\alpha^{(2)}y^{(2)})y^{(1)}
α(1)=(ζ−α(2)y(2))y(1) 且
y
(
i
)
2
=
1
{y^{(i)}}^2=1
y(i)2=1。
W ( α ( 2 ) ) = 1 2 K 11 ( ζ − α ( 2 ) y ( 2 ) ) 2 + 1 2 K 22 α ( 2 ) 2 + y ( 2 ) K 12 ( ζ − α ( 2 ) y ( 2 ) ) α ( 2 ) − ( ( ζ − α ( 2 ) y ( 2 ) ) y ( 1 ) + α ( 2 ) ) + ( ζ − α ( 2 ) y ( 2 ) ) v 1 + y ( 2 ) α ( 2 ) v 2 \begin{split} W(\alpha^{(2)})&=\frac{1}{2}K_{11}(\zeta-\alpha^{(2)}y^{(2)})^2+\frac{1}{2}K_{22}{\alpha^{(2)}}^{2}+y^{(2)}K_{12}(\zeta-\alpha^{(2)}y^{(2)})\alpha^{(2)}\\ &-((\zeta-\alpha^{(2)}y^{(2)})y^{(1)}+\alpha^{(2)})+(\zeta-\alpha^{(2)}y^{(2)})v_1+y^{(2)}\alpha^{(2)}v_2 \end{split} W(α(2))=21K11(ζ−α(2)y(2))2+21K22α(2)2+y(2)K12(ζ−α(2)y(2))α(2)−((ζ−α(2)y(2))y(1)+α(2))+(ζ−α(2)y(2))v1+y(2)α(2)v2
对
α
(
2
)
\alpha^{(2)}
α(2)求导:
∂
W
∂
α
(
2
)
=
K
11
α
(
2
)
+
K
22
α
(
2
)
−
2
K
12
α
(
2
)
−
K
11
ζ
y
(
2
)
+
K
12
ζ
y
(
2
)
+
y
(
1
)
y
(
2
)
−
1
−
v
1
y
(
2
)
+
y
(
2
)
v
2
\frac{\partial W}{\partial \alpha^{(2)}}=K_{11}\alpha^{(2)}+K_{22}\alpha^{(2)}-2K_{12}\alpha^{(2)}-K_{11}\zeta y^{(2)}+K_{12}\zeta y^{(2)}+y^{(1)}y^{(2)}-1-v_{1}y^{(2)}+y^{(2)}v_2
∂α(2)∂W=K11α(2)+K22α(2)−2K12α(2)−K11ζy(2)+K12ζy(2)+y(1)y(2)−1−v1y(2)+y(2)v2
令其为0,得到: ( K 11 + K 22 − 2 K 12 ) α ( 2 ) = y ( 2 ) ( y ( 2 ) − y ( 1 ) + ζ K 11 − ζ K 12 + v 1 − v 2 ) = y ( 2 ) ( y ( 2 ) − y ( 1 ) + ζ K 11 − ζ K 12 + ( g ( x 1 ) − ∑ j = 1 2 α ( j ) y ( j ) K 1 j − b ) − ( g ( x 2 ) − ∑ j = 1 2 α ( j ) y ( j ) K 2 j − b ) ) \begin{split} &(K_{11}+K_{22}-2K_{12})\alpha^{(2)}=y^{(2)}(y^{(2)}-y^{(1)}+\zeta K_{11}-\zeta K_{12}+v_1-v_2)\\ &=y^{(2)}(y^{(2)}-y^{(1)}+\zeta K_{11}-\zeta K_{12}+(g(x_1)-\sum_{j=1}^2\alpha^{(j)}y^{(j)}K_{1j}-b)-(g(x_2)-\sum_{j=1}^2\alpha^{(j)}y^{(j)}K_{2j}-b)) \end{split} (K11+K22−2K12)α(2)=y(2)(y(2)−y(1)+ζK11−ζK12+v1−v2)=y(2)(y(2)−y(1)+ζK11−ζK12+(g(x1)−j=1∑2α(j)y(j)K1j−b)−(g(x2)−j=1∑2α(j)y(j)K2j−b))
将
ζ
=
α
o
l
d
(
1
)
y
(
1
)
+
α
o
l
d
(
2
)
y
(
2
)
\zeta=\alpha_{old}^{(1)}y^{(1)}+\alpha_{old}^{(2)}y^{(2)}
ζ=αold(1)y(1)+αold(2)y(2)代入,得到:
(
K
11
+
K
22
−
2
K
12
)
α
n
e
w
,
u
n
c
(
2
)
=
y
(
2
)
(
(
K
11
+
K
22
−
2
K
12
)
α
o
l
d
(
2
)
y
(
2
)
+
y
(
2
)
−
y
(
1
)
+
g
(
x
1
)
−
g
(
x
2
)
)
=
(
K
11
+
K
22
−
2
K
12
)
α
o
l
d
(
2
)
+
y
(
2
)
(
E
1
−
E
2
)
\begin{split} (K_{11}+K_{22}-2K_{12})\alpha_{new,unc}^{(2)}&=y^{(2)}((K_{11}+K_{22}-2K_{12})\alpha_{old}^{(2)}y^{(2)}+y^{(2)}-y^{(1)}+g(x_1)-g(x_2))\\ &=(K_{11}+K_{22}-2K_{12})\alpha_{old}^{(2)}+y^{(2)}(E_1-E_2) \end{split}
(K11+K22−2K12)αnew,unc(2)=y(2)((K11+K22−2K12)αold(2)y(2)+y(2)−y(1)+g(x1)−g(x2))=(K11+K22−2K12)αold(2)+y(2)(E1−E2)
令
η
=
K
11
+
K
22
−
2
K
12
\eta=K_{11}+K_{22}-2K_{12}
η=K11+K22−2K12代入,得到:
α
n
e
w
,
u
n
c
(
2
)
=
α
o
l
d
(
2
)
+
y
(
2
)
(
E
1
−
E
2
)
η
\alpha_{new,unc}^{(2)}=\alpha_{old}^{(2)}+\frac{y^{(2)}(E_1-E_2)}{\eta}
αnew,unc(2)=αold(2)+ηy(2)(E1−E2)
上面的结果我们求得的是无约束的解,我们需要看一个经过约束条件后的迭代条件。条件如下:
{
α
1
y
1
+
α
2
y
2
=
ζ
0
≤
α
1
≤
C
0
≤
α
2
≤
C
\left\{ \begin{split} &\alpha_1y_1+\alpha_2y_2=\zeta\\ &0\leq \alpha_1\leq C\\ &0\leq \alpha_2\leq C\\ \end{split} \right.
⎩
⎨
⎧α1y1+α2y2=ζ0≤α1≤C0≤α2≤C
我们分情况讨论:
y 1 = y 2 y_1=y_2 y1=y2: α 1 + α 2 = y 1 ζ = k \alpha_1+\alpha_2=y_1\zeta=k α1+α2=y1ζ=k
y 1 ≠ y 2 y_1\neq y_2 y1=y2: α 1 − α 2 = y 1 ζ = k \alpha_1-\alpha_2=y_1\zeta=k α1−α2=y1ζ=k
我们对于第一种情况:
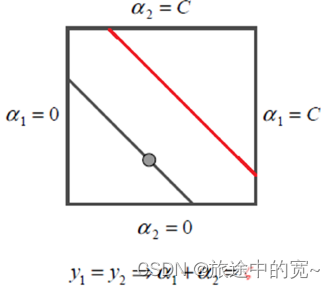
此时的区间为: L = max ( 0 , ζ − C ) = max ( 0 , α o l d ( 2 ) + α o l d ( 1 ) − C ) H = min ( C , ζ ) = min ( C , α o l d ( 2 ) + α o l d ( 1 ) ) \begin{split} &L=\max(0,\zeta-C)=\max(0,\alpha_{old}^{(2)}+\alpha_{old}^{(1)}-C)\\ &H=\min(C,\zeta)=\min(C,\alpha_{old}^{(2)}+\alpha_{old}^{(1)}) \end{split} L=max(0,ζ−C)=max(0,αold(2)+αold(1)−C)H=min(C,ζ)=min(C,αold(2)+αold(1))
我们对于第二种情况:
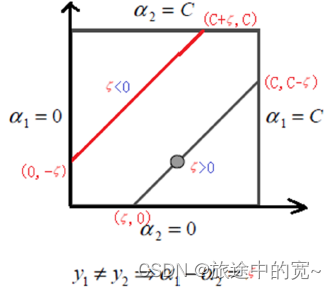
此时的区间为: L = max ( 0 , − ζ ) = max ( 0 , α o l d ( 2 ) − α o l d ( 1 ) ) H = min ( C , C − ζ ) = min ( C , C + α o l d ( 2 ) − α o l d ( 1 ) ) \begin{split} &L=\max(0,-\zeta)=\max(0,\alpha_{old}^{(2)}-\alpha_{old}^{(1)})\\ &H=\min(C,C-\zeta)=\min(C,C+\alpha_{old}^{(2)}-\alpha_{old}^{(1)}) \end{split} L=max(0,−ζ)=max(0,αold(2)−αold(1))H=min(C,C−ζ)=min(C,C+αold(2)−αold(1))
我们的 α ( 2 ) \alpha^{(2)} α(2)的区间为: L ≤ α ( 2 ) ≤ H L\leq \alpha^{(2)}\leq H L≤α(2)≤H
因此我们得到的最终的 α ( 2 ) \alpha^{(2)} α(2)的解为: α n e w ( 2 ) = { H , α n e w , u n c ( 2 ) > H α n e w , u n c ( 2 ) , L ≤ α n e w , u n c ( 2 ) ≤ H L , α n e w , u n c ( 2 ) < L \alpha_{new}^{(2)}=\left\{ \begin{split} &H\;,\;\alpha_{new,unc}^{(2)}>H\\ &\alpha_{new,unc}^{(2)}\;,\;L\leq \alpha_{new,unc}^{(2)}\leq H\\ &L\;,\;\alpha_{new,unc}^{(2)}<L \end{split} \right. αnew(2)=⎩ ⎨ ⎧H,αnew,unc(2)>Hαnew,unc(2),L≤αnew,unc(2)≤HL,αnew,unc(2)<L
求得
α
n
e
w
(
1
)
\alpha_{new}^{(1)}
αnew(1)为:
α
n
e
w
(
1
)
=
α
o
l
d
(
1
)
+
y
(
1
)
y
(
2
)
(
α
o
l
d
(
2
)
−
α
n
e
w
(
2
)
)
\alpha_{new}^{(1)}=\alpha_{old}^{(1)}+y^{(1)}y^{(2)}(\alpha_{old}^{(2)}-\alpha_{new}^{(2)})
αnew(1)=αold(1)+y(1)y(2)(αold(2)−αnew(2))
我们接下来是计算 b b b值,我们有: g ( x ) = ∑ i = 1 m α ( i ) y ( i ) K ( x ( i ) , x ) + b E i = g ( x ( i ) ) − y ( i ) = ( ∑ j = 1 m α ( j ) y ( j ) K ( x ( j ) , x ( i ) ) + b ) − y ( i ) \begin{split} &g(x)=\sum_{i=1}^{m}\alpha^{(i)}y^{(i)}K(x^{(i)},x)+b\\ &E_i=g(x^{(i)})-y^{(i)}=(\sum_{j=1}^{m}\alpha^{(j)}y^{(j)}K(x^{(j)},x^{(i)})+b)-y^{(i)} \end{split} g(x)=i=1∑mα(i)y(i)K(x(i),x)+bEi=g(x(i))−y(i)=(j=1∑mα(j)y(j)K(x(j),x(i))+b)−y(i)
(1)当
0
<
α
n
e
w
(
1
)
<
C
0<\alpha_{new}^{(1)}<C
0<αnew(1)<C时,有:
∑
i
=
1
m
y
(
i
)
α
(
i
)
K
i
1
+
b
=
y
(
1
)
\sum_{i=1}^{m}y^{(i)}\alpha^{(i)}K_{i1}+b=y^{(1)}
i=1∑my(i)α(i)Ki1+b=y(1)
因此:
b
n
e
w
(
1
)
=
y
(
1
)
−
∑
i
=
3
m
y
(
i
)
α
(
i
)
K
i
1
−
α
n
e
w
(
1
)
y
(
1
)
K
11
−
α
n
e
w
(
2
)
y
(
2
)
K
21
b_{new}^{(1)}=y^{(1)}-\sum_{i=3}^{m}y^{(i)}\alpha^{(i)}K_{i1}-\alpha_{new}^{(1)}y^{(1)}K_{11}-\alpha_{new}^{(2)}y^{(2)}K_{21}
bnew(1)=y(1)−i=3∑my(i)α(i)Ki1−αnew(1)y(1)K11−αnew(2)y(2)K21
由
E
1
E_1
E1定义可知:
E
1
=
∑
i
=
3
m
y
(
i
)
α
(
i
)
K
i
1
+
α
o
l
d
(
1
)
y
(
1
)
K
11
+
α
o
l
d
(
2
)
y
(
2
)
K
21
+
b
o
l
d
−
y
(
1
)
E_1=\sum_{i=3}^{m}y^{(i)}\alpha^{(i)}K_{i1}+\alpha_{old}^{(1)}y^{(1)}K_{11}+\alpha_{old}^{(2)}y^{(2)}K_{21}+b_{old}-y^{(1)}
E1=i=3∑my(i)α(i)Ki1+αold(1)y(1)K11+αold(2)y(2)K21+bold−y(1)
变形得:
y
(
1
)
−
∑
i
=
3
m
y
(
i
)
α
(
i
)
K
i
1
=
−
E
1
+
α
o
l
d
(
1
)
y
(
1
)
K
11
+
α
o
l
d
(
2
)
y
(
2
)
K
21
+
b
o
l
d
y^{(1)}-\sum_{i=3}^{m}y^{(i)}\alpha^{(i)}K_{i1}=-E_1+\alpha_{old}^{(1)}y^{(1)}K_{11}+\alpha_{old}^{(2)}y^{(2)}K_{21}+b_{old}
y(1)−i=3∑my(i)α(i)Ki1=−E1+αold(1)y(1)K11+αold(2)y(2)K21+bold
代入
b
n
e
w
(
1
)
=
y
(
1
)
−
∑
i
=
3
m
y
(
i
)
α
(
i
)
K
i
1
−
α
n
e
w
(
1
)
y
(
1
)
K
11
−
α
n
e
w
(
2
)
y
(
2
)
K
21
b_{new}^{(1)}=y^{(1)}-\sum_{i=3}^{m}y^{(i)}\alpha^{(i)}K_{i1}-\alpha_{new}^{(1)}y^{(1)}K_{11}-\alpha_{new}^{(2)}y^{(2)}K_{21}
bnew(1)=y(1)−∑i=3my(i)α(i)Ki1−αnew(1)y(1)K11−αnew(2)y(2)K21得:
b
n
e
w
(
1
)
=
−
E
1
−
y
(
1
)
K
11
(
α
n
e
w
(
1
)
−
α
o
l
d
(
1
)
)
−
y
(
2
)
K
21
(
α
n
e
w
(
2
)
−
α
o
l
d
(
2
)
)
+
b
o
l
d
b_{new}^{(1)}=-E_1-y^{(1)}K_{11}(\alpha_{new}^{(1)}-\alpha_{old}^{(1)})-y^{(2)}K_{21}(\alpha_{new}^{(2)}-\alpha_{old}^{(2)})+b_{old}
bnew(1)=−E1−y(1)K11(αnew(1)−αold(1))−y(2)K21(αnew(2)−αold(2))+bold
(2)同理若
0
<
α
n
e
w
(
2
)
<
C
0<\alpha_{new}^{(2)}<C
0<αnew(2)<C,可得:
b
n
e
w
(
2
)
=
−
E
2
−
y
(
1
)
K
12
(
α
n
e
w
(
1
)
−
α
o
l
d
(
1
)
)
−
y
(
2
)
K
22
(
α
n
e
w
(
2
)
−
α
o
l
d
(
2
)
)
+
b
o
l
d
b_{new}^{(2)}=-E_2-y^{(1)}K_{12}(\alpha_{new}^{(1)}-\alpha_{old}^{(1)})-y^{(2)}K_{22}(\alpha_{new}^{(2)}-\alpha_{old}^{(2)})+b_{old}
bnew(2)=−E2−y(1)K12(αnew(1)−αold(1))−y(2)K22(αnew(2)−αold(2))+bold
(3)若
α
n
e
w
(
1
)
\alpha_{new}^{(1)}
αnew(1)和
α
n
e
w
(
2
)
\alpha_{new}^{(2)}
αnew(2)同时满足
0
<
α
n
e
w
(
i
)
<
C
0<\alpha_{new}^{(i)}<C
0<αnew(i)<C,则:
b
n
e
w
(
1
)
=
b
n
e
w
(
2
)
b_{new}^{(1)}=b_{new}^{(2)}
bnew(1)=bnew(2)
若
α
n
e
w
(
1
)
\alpha_{new}^{(1)}
αnew(1)和
α
n
e
w
(
2
)
\alpha_{new}^{(2)}
αnew(2)是0或者
C
C
C,则:
b
n
e
w
=
b
n
e
w
(
1
)
+
b
n
e
w
(
2
)
2
b_{new}=\frac{b_{new}^{(1)}+b_{new}^{(2)}}{2}
bnew=2bnew(1)+bnew(2)
3.SMO算法推导结果
g ( x ) = ∑ i = 1 m α ( i ) y ( i ) K ( x ( i ) , x ) + b E i = g ( x ( i ) ) − y ( i ) = ( ∑ j = 1 m α ( j ) y ( j ) K ( x ( j ) , x ( i ) ) + b ) − y ( i ) η = K 11 + K 22 − 2 K 12 α n e w , u n c ( 2 ) = α o l d ( 2 ) + y ( 2 ) ( E 1 − E 2 ) η \begin{split} &g(x)=\sum_{i=1}^{m}\alpha^{(i)}y^{(i)}K(x^{(i)},x)+b\\ &E_i=g(x^{(i)})-y^{(i)}=(\sum_{j=1}^{m}\alpha^{(j)}y^{(j)}K(x^{(j)},x^{(i)})+b)-y^{(i)}\\ &\eta=K_{11}+K_{22}-2K_{12}\\ &\alpha_{new,unc}^{(2)}=\alpha_{old}^{(2)}+\frac{y^{(2)}(E_1-E_2)}{\eta} \end{split} g(x)=i=1∑mα(i)y(i)K(x(i),x)+bEi=g(x(i))−y(i)=(j=1∑mα(j)y(j)K(x(j),x(i))+b)−y(i)η=K11+K22−2K12αnew,unc(2)=αold(2)+ηy(2)(E1−E2)
若 y ( 1 ) ≠ y ( 2 ) y^{(1)}\neq y^{(2)} y(1)=y(2): L = max ( 0 , − ζ ) = max ( 0 , α o l d ( 2 ) − α o l d ( 1 ) ) H = min ( C , C − ζ ) = min ( C , C + α o l d ( 2 ) − α o l d ( 1 ) ) \begin{split} &L=\max(0,-\zeta)=\max(0,\alpha_{old}^{(2)}-\alpha_{old}^{(1)})\\ &H=\min(C,C-\zeta)=\min(C,C+\alpha_{old}^{(2)}-\alpha_{old}^{(1)}) \end{split} L=max(0,−ζ)=max(0,αold(2)−αold(1))H=min(C,C−ζ)=min(C,C+αold(2)−αold(1))
若 y ( 1 ) = y ( 2 ) y^{(1)}=y^{(2)} y(1)=y(2): L = max ( 0 , ζ − C ) = max ( 0 , α o l d ( 2 ) + α o l d ( 1 ) − C ) H = min ( C , ζ ) = min ( C , α o l d ( 2 ) + α o l d ( 1 ) ) \begin{split} &L=\max(0,\zeta-C)=\max(0,\alpha_{old}^{(2)}+\alpha_{old}^{(1)}-C)\\ &H=\min(C,\zeta)=\min(C,\alpha_{old}^{(2)}+\alpha_{old}^{(1)}) \end{split} L=max(0,ζ−C)=max(0,αold(2)+αold(1)−C)H=min(C,ζ)=min(C,αold(2)+αold(1))
α n e w ( 2 ) = { H , α n e w , u n c ( 2 ) > H α n e w , u n c ( 2 ) , L ≤ α n e w , u n c ( 2 ) ≤ H L , α n e w , u n c ( 2 ) < L \alpha_{new}^{(2)}=\left\{ \begin{split} &H\;\;,\;\;\alpha_{new,unc}^{(2)}>H\\ &\alpha_{new,unc}^{(2)}\;\;,\;\;L\leq \alpha_{new,unc}^{(2)}\leq H\\ &L\;\;,\;\;\alpha_{new,unc}^{(2)}<L \end{split} \right. αnew(2)=⎩ ⎨ ⎧H,αnew,unc(2)>Hαnew,unc(2),L≤αnew,unc(2)≤HL,αnew,unc(2)<L
α n e w ( 1 ) = α o l d ( 1 ) + y ( 1 ) y ( 2 ) ( α o l d ( 2 ) − α n e w ( 2 ) ) b n e w ( 1 ) = − E 1 − y ( 1 ) K 11 ( α n e w ( 1 ) − α o l d ( 1 ) ) − y ( 2 ) K 21 ( α n e w ( 2 ) − α o l d ( 2 ) ) b n e w ( 2 ) = − E 2 − y ( 1 ) K 12 ( α n e w ( 1 ) − α o l d ( 1 ) ) − y ( 2 ) K 22 ( α n e w ( 2 ) − α o l d ( 2 ) ) \begin{split} &\alpha_{new}^{(1)}=\alpha_{old}^{(1)}+y^{(1)}y^{(2)}(\alpha_{old}^{(2)}-\alpha_{new}^{(2)})\\ &b_{new}^{(1)}=-E_1-y^{(1)}K_{11}(\alpha_{new}^{(1)}-\alpha_{old}^{(1)})-y^{(2)}K_{21}(\alpha_{new}^{(2)}-\alpha_{old}^{(2)})\\ &b_{new}^{(2)}=-E_2-y^{(1)}K_{12}(\alpha_{new}^{(1)}-\alpha_{old}^{(1)})-y^{(2)}K_{22}(\alpha_{new}^{(2)}-\alpha_{old}^{(2)}) \end{split} αnew(1)=αold(1)+y(1)y(2)(αold(2)−αnew(2))bnew(1)=−E1−y(1)K11(αnew(1)−αold(1))−y(2)K21(αnew(2)−αold(2))bnew(2)=−E2−y(1)K12(αnew(1)−αold(1))−y(2)K22(αnew(2)−αold(2))
若 0 < α n e w ( 1 ) < C 0<\alpha_{new}^{(1)}<C 0<αnew(1)<C,则: b = b n e w ( 1 ) b=b_{new}^{(1)} b=bnew(1)
若 0 < α n e w ( 2 ) < C 0<\alpha_{new}^{(2)}<C 0<αnew(2)<C,则: b = b n e w ( 2 ) b=b_{new}^{(2)} b=bnew(2)
其他情况:
b
n
e
w
=
b
n
e
w
(
1
)
+
b
n
e
w
(
2
)
2
b_{new}=\frac{b_{new}^{(1)}+b_{new}^{(2)}}{2}
bnew=2bnew(1)+bnew(2)
)}K_{22}(\alpha_{new}{(2)}-\alpha_{old}{(2)})
\end{split}$$
若 0 < α n e w ( 1 ) < C 0<\alpha_{new}^{(1)}<C 0<αnew(1)<C,则: b = b n e w ( 1 ) b=b_{new}^{(1)} b=bnew(1)
若 0 < α n e w ( 2 ) < C 0<\alpha_{new}^{(2)}<C 0<αnew(2)<C,则: b = b n e w ( 2 ) b=b_{new}^{(2)} b=bnew(2)
其他情况: b n e w = b n e w ( 1 ) + b n e w ( 2 ) 2 b_{new}=\frac{b_{new}^{(1)}+b_{new}^{(2)}}{2} bnew=2bnew(1)+bnew(2)






















 3623
3623











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










