主成分分析(Principal Components Analysis, PCA)是一个简单的机器学习算法,可以通过基础的线性代数知识推导。
假设在Rn空间中我们有m个点{x(1),…,x(m)},我们希望对这些点进行有损压缩。有损压缩表示我们使用更少的内存,但损失一些精度去存储这些点。我们希望损失的精度尽可能少。
一种编码这些点的方式是用低维表示。对于每个点x(i)∈Rn,会有一个对应的编码向量c(i)∈Rl。如果l比n小,那么我们便使用了更少的内存来存储原来的数据。我们希望找到一个编码函数,根据输入返回编码,f(x)=c;我们也希望找到一个解码函数,给定编码重构输入,x≈g(f(x)).
PCA由我们选择的解码函数而定。具体地,为了简化解码器,我们使用矩阵乘法将编码映射回Rn,即g(c)=Dc,其中D∈Rn*l是定义解码的矩阵。
目前为止所描述的问题,可能会有多个解。因为如果我们按比例地缩小所有点对应的编码向量ci,那么我们只需按比例放大D:,i,即可保持结果不变。为了使问题有唯一解,我们限制D中所有列向量都有单位范数(unit norm)。
计算这个解码器的最优编码可能是一个困难的问题。为了使编码问题简单一些,PCA限制D的列向量彼此正交(注意,除非l=n,否则严格意义上D不是一个正交矩阵)。
为了将这个基本想法变为我们能够实现的算法,首先我们需要明确如果根据每一个输入x得到一个最优编码c*。一种方法是最小化原始输入向量x和重构向量g(c*)之间的距离。我们使用范数来衡量它们之间的距离。在PCA算法中,我们使用L2范数:
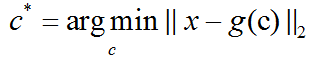
我们可以用平方L2范数替代L2范数,因为两者在相同的值c上取得最小值。这是因为L2范数是非负的,并且平方运算在非负值上是单调递增的。
主成分分析(PCA):PCA算法提供了一种压缩数据的方式,也可以将PCA视为学习数据表示的无监督学习算法。PCA学习一种比原始输入维数更低的表示。它也学习了一种元素之间彼此没有线性相关的表示。PCA可以通过协方差矩阵得到。主成分也可以通过奇异值分解(SVD)得到。
在多元统计分析中,PCA是一种分析、简化数据集的技术。主成分分析经常用于减少数据集的维数,同时保持数据集中的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是,这也不是一定的,要视具体应用而定。由于主成分分析依赖所给数据,所以数据的准确性对分析结果影响很大。
主成分分析由卡尔•皮尔逊于1901年发明,用于分析数据及建立数理模型。其方法主要是通过对协方差矩阵进行特征分解,以得出数据的主成分(即特征向量)与它们的权值(即特征值)。PCA是最简单的以特征量分析多元统计分布的方法。其结果可以理解为对原数据中的方差做出解释:哪一个方向上的数据值对方差影响最大?换而言之,PCA提供了一种降低数据维度的有效方法;如果分析者在原数据中除掉最小的特征值所对应的成分,那么所得的低维度数据必定是最优化的(也即,这样降低维度必定是失去讯息最少的方法)。主成分分析在分析复杂数据时尤为有用,比如人脸识别。
PCA是最简单的以特征量分析多元统计分布的方法。通常情况下,这种运算可以被看作是揭露数据的内部结构,从而更好的解释数据的变量的方法。如果一个多元数据集能够在一个高维数据空间坐标系中被显现出来,那么PCA就能够提供一幅比较低维度的图像,这幅图像即为在讯息最多的点上原对象的一个”投影”。这样就可以利用少量的主成分使得数据的维度降低了。
PCA的数学定义是:一个正交化线性变换,把数据变换到一个新的坐标系统中,使得这一数据的任何投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。
定义一个n*m的矩阵,XT为去平均值(以平均值为中心移动至原点)的数据,其行为数据样本,列为数据类别(注意,这里定义的是XT而不是X)。则X的奇异值分解为X=WΣVT,其中m*m矩阵W是XXT的本征矢量矩阵,Σ是m*n的非负矩形对角矩阵,V是n*n的XTX的本征矢量矩阵。据此,YT=XTW=VΣTWTW=VΣT,当m<n-1时,V在通常情况下不是唯一定义的,而Y则是唯一定义的。W是一个正交矩阵,YT是XT的转置,且YT的第一列由第一主成分组成,第二列由第二主成分组成,依次类推。
为了得到一种降低数据维度的有效办法,我们可以利用WL把X映射到一个只应用前面L个向量的低维空间中去:Y=WLTX=ΣLVT,其中ΣL=IL*mΣ,且IL*m为L*m的单位矩阵。X的单向量矩阵W相当于协方差矩阵的本征矢量C=XXT, XXT=WΣΣTWT.
在欧几里得空间给定一组点数,第一主成分对应于通过多维空间平均点的一条线,同时保证各个点到这条直线距离的平方和最小。去除掉第一主成分后,用同样的方法得到第二主成分。依次类推。在Σ中的奇异值均为矩阵XXT的本征值的平方根。每一个本征值都与跟它们相关的方差是成正比的,而且所有本征值的总和等于所有点到它们的多维空间平均点距离的平方和。PCA提供了一种降低维度的有效办法,本质上,它利用正交变换将围绕平均点的点集中尽可能多的变量投影到第一维中去,因此,降低维度必定是失去讯息最少的方法。PCA具有保持子空间拥有最大方差的最优正交变换的特性。然而,当与离散余弦变换相比时,它需要更大的计算需求代价。非线性降维技术相对于PCA来说则需要更高的计算要求。
PCA对变量的缩放很敏感。如果我们只有两个变量,而且它们具有相同的样本方差,并且成正相关,那么PCA将涉及两个变量的主成分的旋转。但是,如果把第一个变量的所有值都乘以100,那么第一主成分就几乎和这个变量一样,另一个变量只提供了很小的贡献,第二主成分也将和第二个原始变量几乎一致。这就意味着当不同的变量代表不同的单位(如温度和质量)时,PCA是一种比较武断的分析方法。一种使PCA不那么武断的方法是使用变量缩放以得到单位方差。
通常,为了确保第一主成分描述的是最大方差的方向,我们会使用平均减法进行主成分分析。如果不执行平均减法,第一主成分有可能或多或少的对应于数据的平均值。另外,为了找到近似数据的最小均方误差,我们必须选取一个零均值。
主成分分析的属性和限制:主成分分析的结果取决于变量的缩放。主成分分析的适用性受到由它的派生物产生的某些假设的限制。
主成分分析和信息理论:通过使用降维来保存大部分数据信息的主成分分析的观点是不正确的。确实如此,当没有任何假设信息的信号模型时,主成分分析在降维的同时并不能保证信息的不丢失,其中信息是由香农熵来衡量的。基于假设得x=s+n也就是说,向量x是含有信息的目标信号s和噪声信号n之和,从信息论角度考虑主成分分析在降维上是最优的。
主成分分析(PCA)是一种能够极大提升无监督特征学习速度的数据降维算法。更重要的是,理解PCA算法,对实现白化算法有很大的帮助,很多算法都先用白化算法作预处理步骤。假设你使用图像来训练算法,因为图像中相邻的像素高度相关,输入数据是有一定冗余的。具体来说,假如我们正在训练的16*16灰度值图像,记为一个256维向量x∈R256,其中特征值xj对应每个像素的亮度值。由于相邻像素间的相关性,PCA算法可以将输入向量转换为一个维数低很多的近似向量,而且误差非常小。
选择主成分个数:决定k值时,我们通常会考虑不同k值可保留的方差百分比。具体来说,如果k=n,那么我们得到的是对数据的完美近似,也就是保留了100%的方差,即原始数据的所有变化都被保留下来;相反,如果k=0,那等于是使用零向量来逼近输入数据,也就是只有0%的方差被保留下来。一般而言,设λ1,λ2,…,λn表示Σ的特征值(按由大到小顺序排列),使得λj为对应于特征向量uj的特征值。那么如果我们保留前k个成分,则保留的方差百分比可计算为:
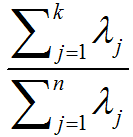
以处理图像数据为例,一个惯常的经验法则是选择k以保留99%的方差。对其它应用,如不介意引入稍大的误差,有时也保留90-98%的方差范围。
对图像数据应用PCA算法:为使PCA算法能有效工作,通常我们希望所有的特征x1,x2,…,xn都有相似的取值范围(并且均值接近于0)。如果你曾在其它应用中使用过PCA算法,你可能知道有必要单独对每个特征做预处理,即通过估算每个特征xj的均值和方差,而后将其取值范围规整化为零均值和单位方差。但是,对于大部分图像类型,我们却不需要进行这样的预处理。假定我们将在自然图像上训练算法,此时特征xj代表的是像素j的值。所谓”自然图像”,不严格的说,是指人或动物在他们一生中所见的那种图像。
注:通常我们选取含草木等内容的户外场景图片,然后从中随机截取小图像块(如16*16像素)来训练算法。在实践中我们发现,大多数特征学习算法对训练图片的确切类型并不敏感,所以大多数用普通照相机拍摄的图片,只要不是特别的模糊或带有非常奇怪的人工痕迹,都可以使用。
在自然图像上进行训练时,对每一个像素单独估计均值和方差意义不大,因为(理论上)图像任一部分的统计性质都应该和其它部分相同,图像的这种特性被称作平稳性(stationarity)。
具体而言,为使PCA算法正常工作,我们通常需要满足以下要求:(1)、特征的均值大致为0;(2)、不同特征的方差值彼此相似。对于自然图片,即使不进行方差归一化操作,条件(2)也自然满足,故而我们不再进行任何方差归一化操作(对音频数据,如声谱,或文本数据,如词袋向量,我们通常也不进行方差归一化)。实际上,PCA算法对输入数据具有缩放不变性,无论输入数据的值被如何放大(或缩小),返回的特征向量都不改变。更正式的说:如果将每个特征向量x都乘以某个正数(即所有特征量被放大或缩小相同的倍数),PCA的输出特征向量都将不会发生变化。
既然我们不做方差归一化,唯一还需进行的规整化操作就是均值规整化,其目的是保证所有特征的均值都在0附近。根据应用,在大多数情况下,我们并不关注所输入图像的整体明亮程度。比如在对象识别任务中,图像的整体明亮程度并不会影响图像中存在的是什么物体。更为正式地说,我们对图像块的平均亮度值不感兴趣,所以可以减去这个值来进行均值规整化。具体的步骤是,如果x(i)∈Rn代表16x16的图像块的亮度(灰度)值(n=256),可用如下算法来对每幅图像进行零均值化操作:
请注意:(1)、对每个输入图像块x(i)都要单独执行上面两个步骤;(2)、这里的μ(i)是指图像块x(i)的平均亮度值。尤其需要注意的是,这和为每个像素xj单独估算均值是两个完全不同的概念。
如果你处理的图像并非自然图像(比如,手写文字,或者白背景正中摆放单独物体),其他规整化操作就值得考虑了,而哪种做法最合适也取决于具体应用场合。但对自然图像而言,对每幅图像进行上述的零均值规整化,是默认而合理的处理。以上内容主要摘自: 《深度学习中文版》、维基百科、UFLDL








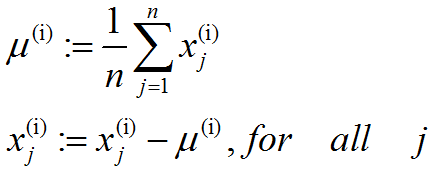














 5344
5344

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








