机器学习之主成分分析（PCA）

Milu.xy

已于 2024-06-18 10:41:55 修改

阅读量1.1k

点赞数 21

文章标签：机器学习人工智能

于 2024-06-18 10:39:10 首次发布

本文链接：https://blog.csdn.net/m0_73614883/article/details/139761152

版权

一、主成分分析（PCA）简介

主成分分析（Principal Component Analysis, PCA）是一种常用的数据降维技术，用于简化数据集，同时保留尽可能多的信息。它通过将原始高维数据转换为较低维度的主成分，从而降低数据的复杂性。这种方法不仅有助于减少计算量，还能帮助我们更容易地可视化和理解数据。

什么是PCA？

PCA是一种线性变换技术，其核心思想是找到数据集中变化最大的方向，即主成分。这些主成分是原始特征的线性组合，按解释方差的大小排序。第一个主成分解释了数据中最多的方差，第二个主成分解释了剩余方差中的最大部分，依此类推。

为什么使用PCA？

降维：在处理高维数据时，PCA能够显著减少维度，简化数据结构，降低计算成本。
去除噪声：通过保留主要特征，PCA可以去除数据中的噪声，提高数据质量。
可视化：PCA将高维数据转换为2D或3D数据，便于可视化分析，帮助我们更直观地理解数据。

二、算法流程

2.1 主要步骤

1. 数据标准化：

将数据中心化，即减去每个特征的均值，使得每个特征的均值为0。
对数据进行标准化处理（可选），即将每个特征除以其标准差，使得数据的尺度一致。

假设数据集为 X，其中 X 是一个 m×n的矩阵，m是样本数，n 是特征数。

标准化后的数据为：

其中是第 j个特征的均值，是第 j个特征的标准差。

2. 计算协方差矩阵：

计算中心化数据的协方差矩阵。协方差矩阵反映了各特征之间的相关性。

中心化后的数据为：

协方差矩阵 Σ 为：

3. 计算特征值和特征向量：

对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。特征值反映了对应特征向量方向上的数据方差大小。

对协方差矩阵 Σ 进行特征值分解：

其中，λ是特征值，v 是对应的特征向量。

4. 选择主成分：

根据特征值的大小排序，选择前k个最大的特征值对应的特征向量。这些特征向量就是新的低维空间的基底，称为主成分。

选择前 k个最大的特征值对应的特征向量，组成一个矩阵 Vk ，其中每列是一个特征向量。

5. 转换数据：

将原始数据投影到选取的主成分上，得到降维后的数据。

将原始数据投影到新的低维空间：

这样，Xnew 就是降维后的数据。

2.2 步骤计算示例

假设我们有一个2维的数据集：

数据标准化：

2. 计算协方差矩阵：

3. 计算特征值和特征向量：

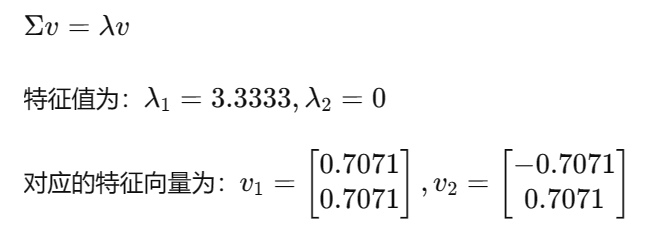
4. 选择主成分：

选择最大的特征值对应的特征向量 v1。

转换数据：

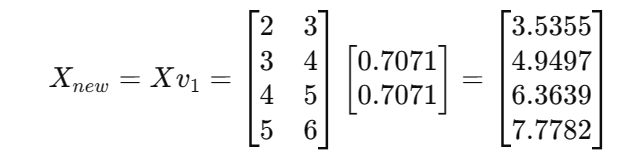
这样，原始数据集就被降维到一维。

三、代码展示

1. 首先，我们需要导入所需的库并加载数据集。这里使用的是著名的Iris数据集。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import time

# 加载示例数据集，这里使用iris数据集
data = load_iris()
X = data.data
y = data.target

2. 计算PCA并记录结果

我们将计算不同主成分数量下的累计解释方差比例、计算时间和重构误差。

# 存储不同主成分数量下的累计解释方差比例和计算时间
explained_variances = []
computation_times = []
reconstruction_errors = []

# 计算PCA并记录每次主成分数量下的累计解释方差比例、计算时间和重构误差
for n_components in range(1, X.shape[1] + 1):
    start_time = time.time()
    pca = PCA(n_components=n_components)
    X_pca = pca.fit_transform(X)
    explained_variances.append(np.sum(pca.explained_variance_ratio_))
    computation_times.append(time.time() - start_time)
    
    # 计算重构误差
    X_reconstructed = pca.inverse_transform(X_pca)
    reconstruction_error = np.mean((X - X_reconstructed) ** 2)
    reconstruction_errors.append(reconstruction_error)

3. 绘制结果图表

接下来，我们绘制累计解释方差比例、计算时间和重构误差的折线图。

# 绘制累计解释方差比例折线图
plt.figure(figsize=(14, 6))

plt.subplot(1, 3, 1)
plt.plot(range(1, X.shape[1] + 1), explained_variances, marker='o')
plt.title('Explained Variance vs. Number of Principal Components')
plt.xlabel('Number of Principal Components')
plt.ylabel('Cumulative Explained Variance Ratio')
plt.xticks(range(1, X.shape[1] + 1))
plt.grid(True)

# 绘制计算时间折线图
plt.subplot(1, 3, 2)
plt.plot(range(1, X.shape[1] + 1), computation_times, marker='o')
plt.title('Computation Time vs. Number of Principal Components')
plt.xlabel('Number of Principal Components')
plt.ylabel('Computation Time (seconds)')
plt.xticks(range(1, X.shape[1] + 1))
plt.grid(True)

# 绘制重构误差折线图
plt.subplot(1, 3, 3)
plt.plot(range(1, X.shape[1] + 1), reconstruction_errors, marker='o')
plt.title('Reconstruction Error vs. Number of Principal Components')
plt.xlabel('Number of Principal Components')
plt.ylabel('Reconstruction Error')
plt.xticks(range(1, X.shape[1] + 1))
plt.grid(True)

plt.tight_layout()
plt.show()

4. 二维PCA散点图

我们将数据降到二维，并绘制散点图来观察不同类别的分布。

# 使用前两主成分进行降维并绘制散点图
pca_2d = PCA(n_components=2)
X_pca_2d = pca_2d.fit_transform(X)

plt.figure(figsize=(8, 6))
plt.scatter(X_pca_2d[:, 0], X_pca_2d[:, 1], c=y, cmap='viridis', edgecolor='k', s=50)
plt.title('2D PCA of Iris Dataset')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.colorbar()
plt.show()

5.完整代码展示

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import time

# 加载示例数据集，这里使用iris数据集
data = load_iris()
X = data.data
y = data.target

# 存储不同主成分数量下的累计解释方差比例和计算时间
explained_variances = []
computation_times = []
reconstruction_errors = []

# 计算PCA并记录每次主成分数量下的累计解释方差比例、计算时间和重构误差
for n_components in range(1, X.shape[1] + 1):
    start_time = time.time()
    pca = PCA(n_components=n_components)
    X_pca = pca.fit_transform(X)
    explained_variances.append(np.sum(pca.explained_variance_ratio_))
    computation_times.append(time.time() - start_time)
    
    # 计算重构误差
    X_reconstructed = pca.inverse_transform(X_pca)
    reconstruction_error = np.mean((X - X_reconstructed) ** 2)
    reconstruction_errors.append(reconstruction_error)

# 绘制累计解释方差比例折线图
plt.figure(figsize=(14, 6))

plt.subplot(1, 3, 1)
plt.plot(range(1, X.shape[1] + 1), explained_variances, marker='o')
plt.title('Explained Variance vs. Number of Principal Components')
plt.xlabel('Number of Principal Components')
plt.ylabel('Cumulative Explained Variance Ratio')
plt.xticks(range(1, X.shape[1] + 1))
plt.grid(True)

# 绘制计算时间折线图
plt.subplot(1, 3, 2)
plt.plot(range(1, X.shape[1] + 1), computation_times, marker='o')
plt.title('Computation Time vs. Number of Principal Components')
plt.xlabel('Number of Principal Components')
plt.ylabel('Computation Time (seconds)')
plt.xticks(range(1, X.shape[1] + 1))
plt.grid(True)

# 绘制重构误差折线图
plt.subplot(1, 3, 3)
plt.plot(range(1, X.shape[1] + 1), reconstruction_errors, marker='o')
plt.title('Reconstruction Error vs. Number of Principal Components')
plt.xlabel('Number of Principal Components')
plt.ylabel('Reconstruction Error')
plt.xticks(range(1, X.shape[1] + 1))
plt.grid(True)

plt.tight_layout()
plt.show()

# 使用前两主成分进行降维并绘制散点图
pca_2d = PCA(n_components=2)
X_pca_2d = pca_2d.fit_transform(X)

plt.figure(figsize=(8, 6))
plt.scatter(X_pca_2d[:, 0], X_pca_2d[:, 1], c=y, cmap='viridis', edgecolor='k', s=50)
plt.title('2D PCA of Iris Dataset')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.colorbar()
plt.show()

四、结果分析

4.1 输出结果图

图一：

图二

4.2 优缺点分析

优点:

降维效果显著：
通过解释方差折线图，我们看到前两个主成分可以解释大部分数据方差，展示了PCA在降维方面的有效性。
特征提取：
前几个主成分解释了大部分方差，表明PCA提取了数据中的主要特征。
可视化：
二维散点图展示了降维后的数据分布，便于观察和分析数据。

缺点:

线性假设：
如果数据不是线性可分的，二维散点图可能无法清晰分离不同类别的数据点，展示了PCA在处理非线性数据时的局限性。
信息丢失：
当主成分数量较少时，累计解释方差比例未达到100%，重构误差较高，说明降维过程中有信息丢失。
解释性差：
PCA转换后的主成分是线性组合，通常缺乏实际意义，难以从业务角度解释

4.3 总结

PCA是一种强大的降维工具，特别适用于高维数据的处理。它可以显著减少数据维度，提高计算效率，并有助于数据的可视化。然而，PCA也有其局限性，例如对非线性数据效果不佳以及主成分解释性差。在实际应用中，选择适当的主成分数量至关重要，以在降维和信息保留之间取得平衡。

通过理解PCA的优缺点，我们可以更好地应用PCA，并在适当的场景中使用其他补充方法，如非线性降维技术（例如t-SNE和UMAP），以获得更好的降维效果。

Milu.xy

关注

21
点赞
踩
25

收藏

觉得还不错? 一键收藏
0
评论
机器学习之主成分分析（PCA）

PCA是一种强大的降维工具，特别适用于高维数据的处理。它可以显著减少数据维度，提高计算效率，并有助于数据的可视化。然而，PCA也有其局限性，例如对非线性数据效果不佳以及主成分解释性差。在实际应用中，选择适当的主成分数量至关重要，以在降维和信息保留之间取得平衡。通过理解PCA的优缺点，我们可以更好地应用PCA，并在适当的场景中使用其他补充方法，如非线性降维技术（例如t-SNE和UMAP），以获得更好的降维效果。
复制链接

扫一扫