LSTM入门学习
原文地址:http://blog.csdn.net/hjimce/article/details/51234311
作者:hjimce
一、相关理论
本篇博文主要讲解LSTM、GRU的前向传导过程;因为我觉得反向求导,只要你根据公式按步骤求偏导数,那么只要学会复合函数的求导法则就可以反向推导出来了。除了CNN中的卷积层、池化层这种稍微比较奇葩的求导之外,深度学习的反向求导都是大同小异,这个以后再总结一篇专门的各种网络层的反向求导,这边就不再详述了(后面我所讲的也只讲LSTM的前向传导),不过RNN的反向求导也需要注意误差需要传导到上一时刻的隐藏层。
众所周知,RNN是深度学习领域用于解决序列问题的神器,从理论的上来说,RNN是可以实现长时间记忆的。然而RNN反向求导会出现梯度弥散,导致我们很难训练网络,对于长时刻记忆总不尽人意,于是就诞生了LSTM。下面用个形象点的例子,解释长短记忆,让我们来看两个英语完形填空题目:
(1)"Jane walked into the room. John walked in too. Jane said hi to ___"。
(2)"Jane walked into the room. John walked in too. It was late in the day, and everyone was walking home after a long day at work. Jane said hi to ___"。
对于上面的两个句子而已,根据上下文信息,可以判断空格需要填入的单词都是:Jane,区别在于第二道题目的句子很长,句子中间多出了好多没用的信息。从理论上来说,RNN经过训练后,对于两个题目都可以预测出正确的答案Jane。然而实际上,因为BPTT在反向传播过程中会出现梯度弥散,将使得你最终训练的模型遇到第二道题目时,不能很准确的给出正确答案;而如果是采用LSTM,那么就可以实现比较长时间的记忆。
这个就像就像我等英语菜鸟和英语高手的区别一样,菜鸟的记忆比较弱,在阅读第二道题目看到句子末尾的时候,因为句子太长,我们早已经忘了句子上半部分的单词Jane。
二、LSTM入门学习
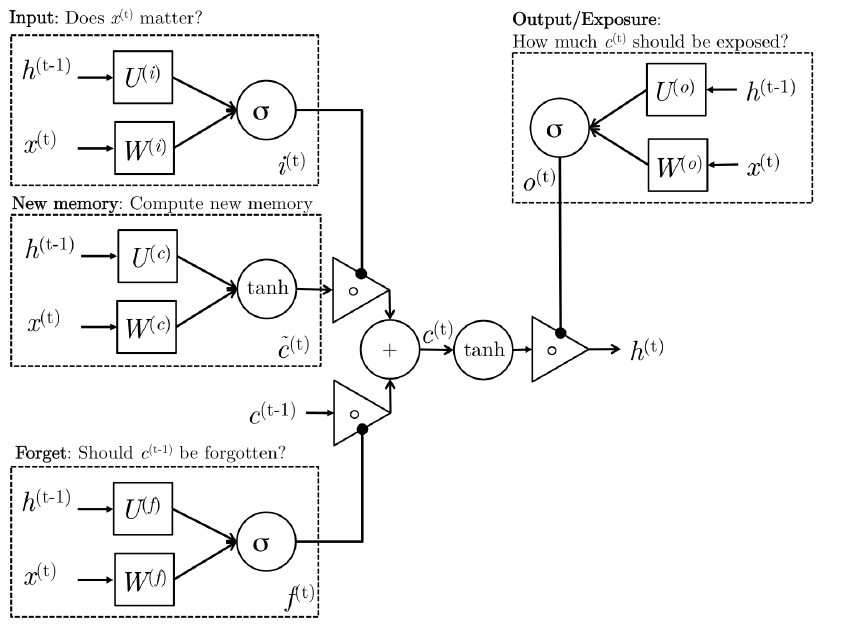
下面先给出LSTM的网络结构图:
看到网络结构图好像很复杂的样子,其实不然,LSTM的网络结构图无非是为了显示其高大上而已,这其实也是一个稍微比RNN难那么一丁点的算法。为了简单起见,下面我将直接先采用公式进行讲解LSTM,省得看见LSTM网络结构图就头晕。
(1)RNN回顾
先简单回顾一下RNN隐层神经元计算公式为:
其中U、W是网络模型的参数,f(.)表示激活函数。RNN隐层神经元的计算由t时刻输入xt,t-1时刻隐层神经元激活值st-1作为输入。总之说白了RNN的核心计算公式就只有上面这么简简单单的公式,所以说会者不难,难者不会,对于已经懂得RNN的人来说,RNN是一个非常简单的网络模型。
(2)LSTM前向传导
相比于RNN来说,LSTM隐层神经元的计算公式稍微复杂一点,LSTM隐藏层前向传导由下面六个计算公式组成,而且其中前4个公式跟上面RNN公式都非常相似:
首先需要先记住上面五个公式中输入变量的含义:
(1)输入变量:x(t)表示t时刻网络的输入数据,S(t-1)表示t-1时刻隐藏层神经元的激活值、C是一个记忆单元
(2)网络参数:U、W都是网络LSTM模型的参数,或者称之为权值矩阵
(3)σ表示sigmoid激活函数
(4)另外s(t)是t时刻,LSTM隐藏层的激活值
从上面的公式我们可以看出LSTM在t时刻的输入包含:X(t)、S(t-1)、C(t-1),输出就是t时刻隐层神经元激活值S(t)。LSTM前四个公式和RNN非常相似,模型都是:
这四个公式的输入都是x(t),s(t-1),每个公式各有各自的参数U、W。前面三个公式的激活函数选择s型函数,大牛门给它们起了一个非常装逼的名词,i、f、o分别称之为输入门、遗忘门、输出门;第4个公式选用tanh激活函数。
1、输入门
输入门可以控制你的输入是否影响你的记忆当中的内容。因变量为i,自变量为:输入数据x(t)、上一时刻隐藏层神经元激活值s(t-1),其采用S激活函数,输出的数值在0~1之间。如果从业余的角度来讲,可以把它看成是一个权值;当i为0的时候,表示当前时刻x(t)的信息被屏蔽,没有存储到记忆中。
2、遗忘门
遗忘门是来看你的记忆是否自我更新保持下去。因变量为f,自变量依旧为:
3、输出门
输出门是影响你的记忆是否被输出出来影响将来这三个们有一个特点:它们的输入数据都是x(t),上一时刻隐藏层的激活值s(t-1),另外这三个们
这种方式使你的记忆得到灵活的保持,而控制记忆如何保持的这些门本身是通过学习得到的,通过不同的任务学习如何去控制这些门。
三、源码实现
https://github.com/fchollet/keras/blob/master/keras/layers/recurrent.py
x_i = K.dot(x * B_W[0], self.W_i) + self.b_i
x_f = K.dot(x * B_W[1], self.W_f) + self.b_f
x_c = K.dot(x * B_W[2], self.W_c) + self.b_c
x_o = K.dot(x * B_W[3], self.W_o) + self.b_o
i = self.inner_activation(x_i + K.dot(h_tm1 * B_U[0], self.U_i))
f = self.inner_activation(x_f + K.dot(h_tm1 * B_U[1], self.U_f))
c = f * c_tm1 + i * self.activation(x_c + K.dot(h_tm1 * B_U[2], self.U_c))
o = self.inner_activation(x_o + K.dot(h_tm1 * B_U[3], self.U_o))
h = o * self.activation(c)
参考文献:
1、http://www.wildml.com/2015/10/recurrent-neural-network-tutorial-part-4-implementing-a-grulstm-rnn-with-python-and-theano/
2、http://colah.github.io/posts/2015-08-Understanding-LSTMs/
3、https://github.com/fchollet/keras/blob/master/keras/layers/recurrent.py
4、《Deep Learning for NLP1》





 本文深入浅出地介绍了长短时记忆网络(LSTM)的基本原理,对比了LSTM与传统循环神经网络(RNN)在处理序列问题上的优势,并详细阐述了LSTM的前向传播过程。此外,还提供了LSTM的实现代码示例。
本文深入浅出地介绍了长短时记忆网络(LSTM)的基本原理,对比了LSTM与传统循环神经网络(RNN)在处理序列问题上的优势,并详细阐述了LSTM的前向传播过程。此外,还提供了LSTM的实现代码示例。
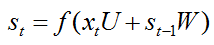
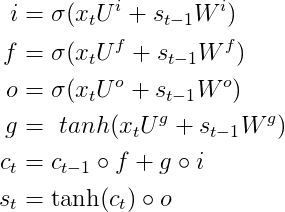
















 2228
2228


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







