Proclaimation:
第一篇博客点击打开链接之后,对LSTM进行了一个较为深入的学习。首先从理论入手,深读了提出模型的原文,大概粗看了二十多篇Paper,关于RNN的问题的产生、LSTM模型的提出和原理,反传的推导之类,还有最近的LSTM的典型应用和性能分析等等。这个报告在我实验室内部小组和其他的小组两次分享过,这边再做一个总结写成博客,跟大家一同探讨。坦率地说,确实是越看越觉得新问题更多。
在这里感谢之前看LSTM的时候入门的两篇博客的作者,
注:这篇博客侧重于对LSTM的理论进行阐述,并不会侧重于模型的讲解,需要一定的对LSTM和RNN的熟悉可能会更好的阅读博客。
LSTM理论推导总结
目录
1. 传统RNN的问题:梯度的消失和爆发
2. LSTM对问题的解决方式
3. LSTM对模型的设计
4. LSTM训练的核心思路和推导
5. 近期LSTM的模型的改进
6. LSTM的工作特性的研究
7. 一些可能存在的问题
8. 总结
9. 参考文献
1.传统RNN模型的问题:梯度的消失和爆发
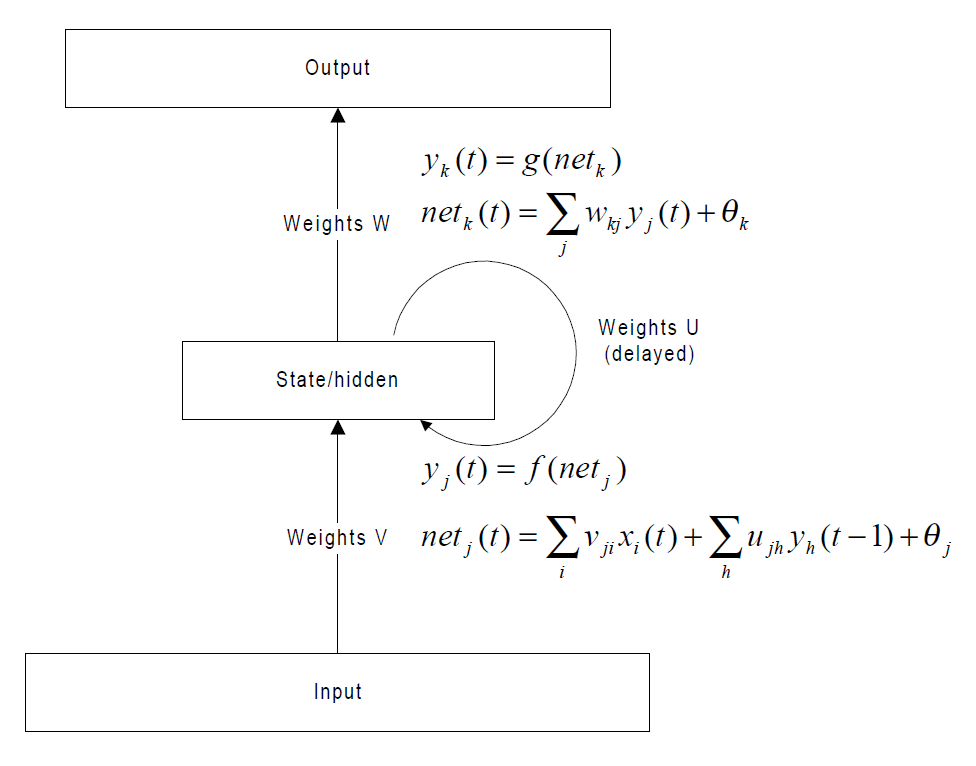
接下来的推导主要源自LSTM的作者的论文《THE VANISHING GRADIENT PROBLEM DURING recurrent neural networks and problem solutions》
以及作者在提出LSTM的论文的前半部分也有一样的内容。
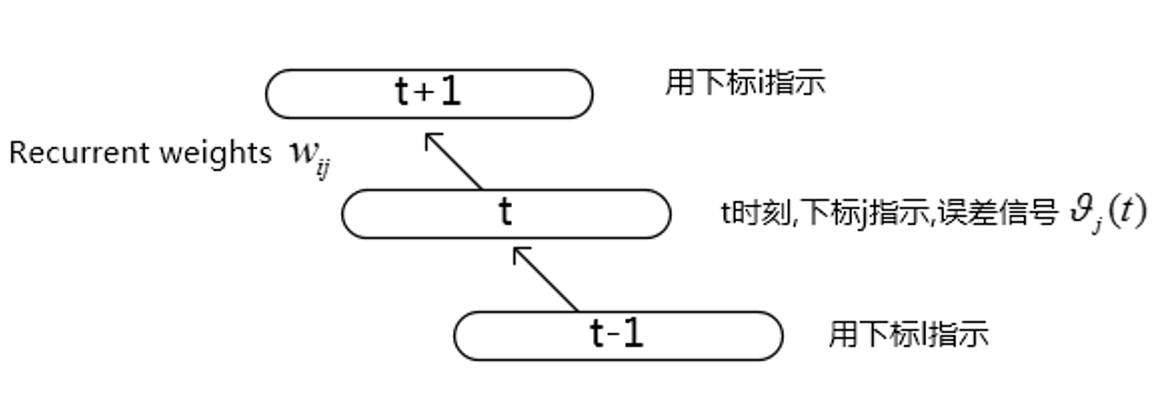
先看一下比较典型的BPTT(Back propgation through time)一个展开的结构,如下图,这里只考虑了部分图。
对于t时刻的误差信号计算如下:
推导公式如下:
上面的公式在整个BPTT乃至整个BP网络里都是非常常见的了。具体推导如下,做个演示:
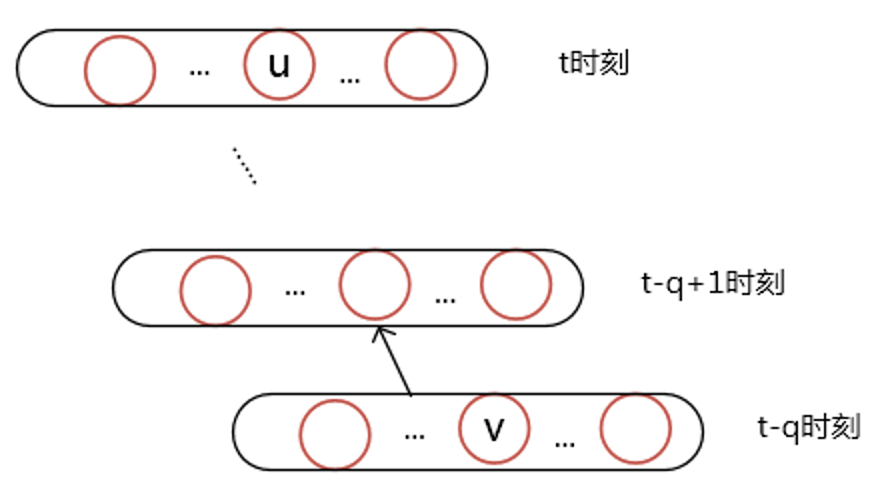
那么如果这个误差信号一直往过去传呢,假设任意两个节点u, v他们的关系是下面这样的:
</








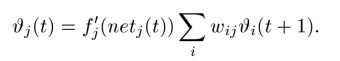
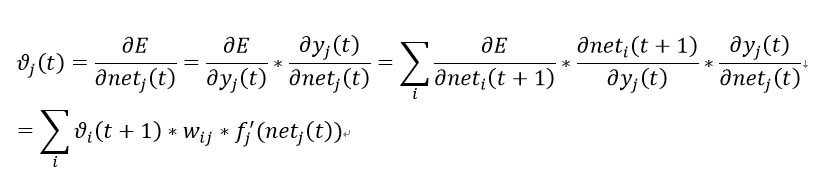
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 445
445

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








