:Blending(混合) and Bagging(自举)
一,Motivation of Aggregation(融合模型的动机)
1,提出Aggregation
假设有T个朋友告诉你将来几天股市的假设,那我们到底选哪一个人的模型好呢?
我们有这么四种选择方法:

所以我们得到的混合模型(AggregationModel):把全部的假设进行混合或者结合,这样可以得出更好的假设。
于是我们就得出了AggregationModel(混合模型)的概念。
2,把Aggregation数学化
把上一幅图化简成数学形式,可以得到:
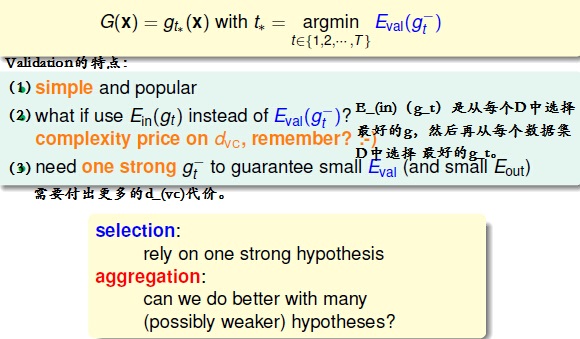
我们复习一下:Selection By Validation:
为什么Aggregation(混合模型)可以工作?他有什么好处呢?
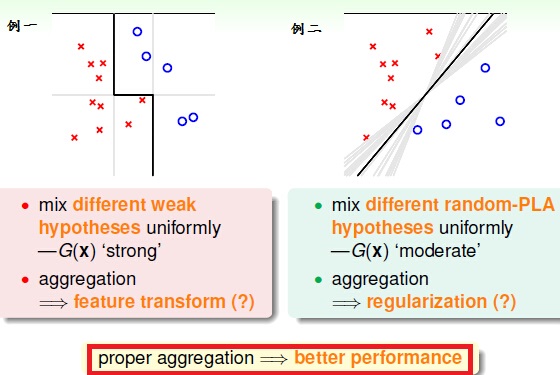
1, 可以把不同的weakhypotheses混合,把模型变得更更好。就有点像feature transform。
2, 选择最好的Hypotheses,就像正则化。
二,Uniform Blending (平均的混合模型)
1,Uniform Blending(Voting) for Classification(均匀混合(投票)的分类)
混合模型分类的数学表示是:
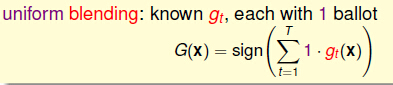
它可以分为几种情况:

2,Uniform Blending(Voting) for Classification(均匀混合(投票)的回归)
混合模型回归的数学表示是:
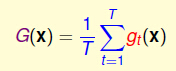
它的优点是:

3,TheoreticalAnalysis of Uniform Blending(均匀混合模型的原理分析)

我们对(1)中的式子进行分析,然后再根据在数据集D中得到g_t的过程,我们可以得到:
因此我们得到Uniform blending的特点是:减小变化,让得到的结果更佳稳定。
三,Linear and any Blending(线性和其他的混合模型)
我们根据第一小节,我们知道linear Blending的一般表达式: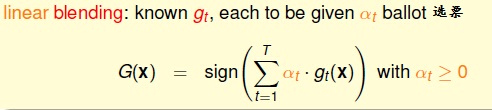
根据G(x),那我们怎么计算α_t??我们通过:
于是我们就知道求解回归的线性混合模型是根据:

那我们看这个式子是不是像regressionSVM中的Linear Regression+transformation的形式呢?

1, 去除constraints
我们已经知道linear Blending(线性混合模型)的基本形式,它与regression SVM的区别在于约束条件(constrain)α_t,那我们想可不可以去除α_t呢?
当α_t小于0时,我们就像解决-g_t,所以我们可以去除约束条件。
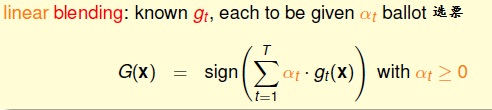
2, Linear Blending versusSelection(线性混合与选择)
我们在解决regression SVM中的Linear Regression+transformation形式的最优g时是采用:

3,对于 any Blending(任意的混合模型)

四,Bagging(Bootstrap Aggregation)[自举的混合模型]
我们在之前学习的是先得到N个g,然后对每个g进行blending。那我们能不能边学习得到不同的g,再根据这些g学到过g^(~)。
我们在第二小节中说到的uniform aggregation(平均融合模型)中的g要diversity(不同),主要采用的方法是:
那我们能不能在同一份资料(D)上,得到不一样的g^(-)呢?

于是我们想到第二讲中的式子(1),把我们的目标与它进行对比:
我们这是运用与统计学里面的自举法(bootstrapping),把一个数据集D中的数据分成D_t个数据。

所以我们得到了BootstrapAggregation(自举混合模型):

因为此方法就像从袋子里面去了N个数据,然后把N个数据放回去,所以我们又称它为:Bagging。

但是做bootstrapping还得注意:

总结:











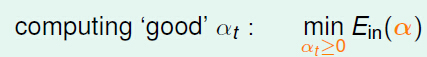


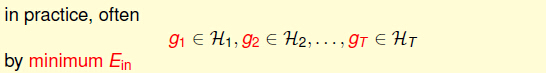
















 3025
3025

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








