BP算法

只限于自己看！

预先说明

首先，这里面什么看成变量，什么看成常量。
变量：网络的权值W（偏置b默认在W内。）以及输入X。
常量：就是target
你可能会说呃呃呃，不是输入都是有值吗，不都是数吗，怎么会是变量啊。。一般来说网络的反向传播就是两种类型。一种是更新网络权值W，这是属于常规的，一种是更新输入X。 不管哪种情况，我们都要把W和X看成变量，才能有反向传播。
推导过程中，W和X都是变量，输出是W和X的函数。

字母说明

• $W_{ij}^{(l)}$:第$l$层到第$l+1$层的权值，并且是$l$层的第$j$个单元到$l+1$层的第$i$个单元的权值。

• $Z_i^{(l)}$:第$l$层的第$i$个结点的输入和。
  显然$Z_i^{(l)}= \sum_{j=0}^{s_{(l-1)}}W_{ij}^{l-1}x_j$ , 其中$s_{l-1}$代表$l-1$层的结点个数（不计算偏置单元)。可以这样说，第0个单元是偏置，1~$s_{(n-1)}$是权重项。

• $a_i^{(l)}$：表示第$l$层的第$i$个结点的激活值，就是下面说的out的输出，或是说$a = f(net)$，写成$a = f(z)$也是一样的。

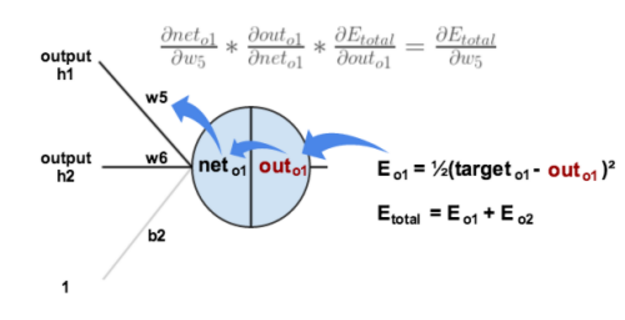
• $\delta_i^{(l)}$: 叫做“残差”，这里表示第$l$层的第$i$个节点的残差。这个非常重要，残差的定义就是——总的代价函数对于某个节点的“net”的偏导。注意的是这里的“net”指的是W*x+b这样的函数结构。可以这样看网络：
  
  现在只需要看每个结点是如何处理数据的。不要看箭头，可以看到，h1和h2再加上“1”共三个结点输入，构成输入$\vec x$, 而相应的权值$\vec W$是$w5$,$w6$,$b2$, 也就是说 $\vec W* \vec x$就是这里的“net”，然后“out”是指激活后的值，就是$f(net)$. 残差就是$\frac{\partial E}{\partial net}$,*不是$\frac{\partial E}{\partial out}$哦！

BP算法细节

参数说明：假设有n层。J表示代价函数，和上面的E是同样的意思，只不过用不同的字母写而已。
1: 首先当然是正向计算咯，分别求出$L_2,L_3,...$直至最后一层$L_n$的激活值。我们这里把输入当做第一层。下面是真正的反向传播。

2: 对于第n层（最后一层是特殊的，必须单独拿出来）每个输出单元$i$,下面的$l$的值为$n$, 计算每个结点的残差：

$$\begin{align} \delta^{(l)}_i =\frac{\partial J(W,b;x,y)}{\partial z_i^{(l)}} = \frac{\partial}{\partial z^{(l)}_i} \;\; \frac{1}{2} \left\|y - h_{W,b}(x)\right\|^2 = - (y_i - a^{(l)}_i) \cdot f'(z^{(l)}_i) \end{align}$$
注意：这里最后乘上了对“net”的导，如果是用sigmoid的函数的话，根据$f'(z^{(l)}_i) = a^{(l)}_i (1- a^{(l)}_i)$, 最后一层的第$i$个结点的残差$\delta_i^{(l)}=-(y_i-a_i^{(l)})\bullet a_i^{(l)}(1-a_i^{(l)})$

3： 从倒数第二层开始，也就是说 $l = n-1, n-2, n - 3,...,2$ 的各层,第$l$层的第$i$个结点的残差计算：

$$\delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i)$$
分析：要想知道第$l$层的第$i$个结点的残差，必须知道该节点所连接的下一层的各个结点的权值，以及这些结点的残差，幸亏第$l+1$层已经计算出来了残差，你只要把后面一层的每个结点$j$的残差乘以该结点与这一层的结点$i$相连的权值，然后加和，最后别忘了乘以这一层的激活方式的导数。 不吹不黑，如果你不太懂得话，这段话可以够你看10遍，你就懂了。

4: 你可能会说要残差干嘛？当然是计算$\frac{\partial J}{\partial w}$和$\frac{\partial J}{\partial b}$用的。
只要：

$$\begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) = a^{(l)}_j \delta_i^{(l+1)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) = \delta_i^{(l+1)} \end{align}$$

结论：求J对“结点j到i的线路”的导数，求出后者i的残差，然后乘以这条线路的流量即可。

分析：其实是这样的，$W_{ij}^l$是第$l$层到$l+1$层的权值，并且是从结点$j$到结点$i$的权值。根据链式法则：

$$\frac{\partial J{(W,b; x, y)}}{\partial w_{ij}^{(l)}} = \frac{\partial J{(W,b; x, y)}}{\partial out_{i}} * \frac{\partial out_{i}}{\partial net_{i}} * \frac{\partial net_{i}}{\partial w_{ij}}$$
请仔细看上面的公式，好好理解。
残差的定义就是$\frac{\partial J{(W,b; x, y)}}{\partial net_{i}}$，根据链式法则：
$$\delta_i^{(l+1）}=\frac{\partial J{(W,b; x, y)}}{\partial net_{i}} = \frac{\partial J{(W,b; x, y)}}{\partial out_{i}} * \frac{\partial out_{i}}{\partial net_{i}}$$ 这下明白了吧，就是说第$l+1$层， $$\frac{\partial J}{\partial w_{ij}^{(l)}}=\delta_i^{(l+1)}* \frac{\partial net_{i}}{\partial w_{ij}}=\delta_i^{(l+1)}a^{(l)}_j$$
注意，第$l+1$层的$\frac{\partial net_{i}}{\partial w_{ij}}$就是该层的输入，也就是第$l$层的输出$a_j^{(l)}$.

最后一个问题，为啥

$$\delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i)$$ 呢?

$$\delta^{(l-1)}_i =\frac{\partial}{\partial z^{(l-1)}_i}J(W,b;x,y) = \frac{\partial}{\partial z^{(l-1)}_i}\frac{1}{2} \left\|y - h_{W,b}(x)\right\|^2 = \frac{\partial}{\partial z^{(l-1)}_i}\frac{1}{2} \sum_{j=1}^{S_{l}}(y_j-a_j^{(l)})^2 \\ = \frac{1}{2} \sum_{j=1}^{S_{l}}\frac{\partial}{\partial z^{(l-1)}_i}(y_j-a_j^{(l)})^2 = \frac{1}{2} \sum_{j=1}^{S_{l}}\frac{\partial}{\partial z^{(l-1)}_i}(y_j-f(z_j^{(l)}))^2 \\ = \sum_{j=1}^{S_{l}}-(y_j-f(z_j^{(l)})) \cdot \frac{\partial}{\partial z_i^{(l-1)}}f(z_j^{(l)}) = \sum_{j=1}^{S_{l}}-(y_j-f(z_j^{(n_l)})) \cdot f'(z_j^{(l)}) \cdot \frac{\partial z_j^{(l)}}{\partial z_i^{(l-1)}} \\ = \sum_{j=1}^{S_{l}} \delta_j^{(l)} \cdot \frac{\partial z_j^{(l)}}{\partial z_i^{(l-1)}} = \sum_{j=1}^{S_{l}} \left(\delta_j^{(l)} \cdot \frac{\partial}{\partial z_i^{(l-1)}}\sum_{k=1}^{S_{(l-1)}}f(z_k^{(l-1)}) \cdot W_{jk}^{(l-1)}\right) \\ = \sum_{j=1}^{S_{l}} \delta_j^{(l)} \cdot W_{ji}^{(l-1)} \cdot f'(z_i^{(l-1)}) = \left(\sum_{j=1}^{S_{l}}W_{ji}^{(l-1)}\delta_j^{(l)}\right)f'(z_i^{(l-1)})$$
慢慢看，看懂问题不大。

编码

1. 进行前馈传导计算，利用前向传导公式，得到 $L_2, L_3, \ldots$ 直到输出层 $L_{l}$ 的激活值。
2. 对输出层（第 $l$层），计算：

   $$\delta^{(n_l)} = - (y - a^{(n_l)}) \bullet f'(z^{(n_l)})$$

3. 对于$l = n_l-1, n_l-2, n_l-3, \ldots, 2$ 的各层，计算：

   $$\delta^{(l)} = \left((W^{(l)})^T \delta^{(l+1)}\right) \bullet f'(z^{(l)})$$

4. 计算最终需要的偏导数值：

   $$\nabla_{W^{(l)}} J(W,b;x,y) = \delta^{(l+1)} (a^{(l)})^T, \\ \nabla_{b^{(l)}} J(W,b;x,y) = \delta^{(l+1)}.$$

最后说明一点，BP传播，计算各层的各点的残差是关键，残差是总的代价函数对于该点的net的偏导，从倒数第二层开始，求残差就要用到其后面的一层的各个残差，只要用后面一层的各个结点残差乘以其与这一层这个的结点所连接的权值，再求和，最后乘以这一层这个结点的out对net的偏导就可以了。如此一来，残差乘以这个结点的输入，就可以得到整个代价函数对于这个结点的w偏导了。