POJ 1330 Nearest Common Ancestors LCA题解

Nearest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 19728		Accepted: 10460

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below: 

 
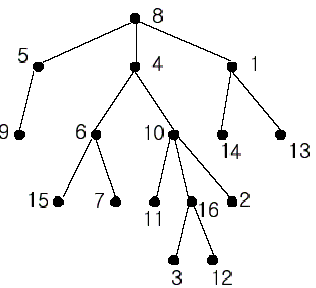
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is. 

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y. 

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3

Source

Taejon 2002

本题是一个多叉树，然后求两点的最近公共单亲节点。

就是典型的LCA问题。这是一个很多解法的，而且被研究的很透彻的问题。

原始的解法：从根节点往下搜索，若果搜索到两个节点分别在一个节点的两边，那么这个点就是最近公共单亲节点了。

Trajan离线算法：首次找到两个节点的时候，如果记录了他们的最低单亲节点，那么答案就是这个最低的单亲节点了。

问题是如何有效记录这个最低单亲节点，并有效根据遍历的情况更新，这就是利用Union Find（并查集）记录已经找到的节点，并及时更新最新访问的节点的当前最低单亲节点。

就是并查集的灵活运用啦，如果学会了并查集那么学这个算法是不难的了。

2015-1-24 update:

下面括号的分析好像有点问题：

(下面是简单思路差不多是暴力法的解法，不过其实相对本题来说就是一次查询，故此这个也是不错的方法，而且平均时间效率不过O(lgn)，应该是很快的了。

不过有思想和这个差不多的，但是更加省内存的方法，就是从需要查找的节点往单亲节点查找，那么速度是一样的，不过省内存，因为只需要记录一个父母节点就可以了，而且程序会简洁点。)

这个方法的基本思想是：

假设要查找u，v的LCA，

递归深度遍历整棵树，这个时候有三种情况：

1. 如果没哟找到u或者v其中一个节点，那么就返回0；

2 如果找到了u或v的其中一个节点，那么就返回找到的节点

3 如果找到u且找到v两个节点，那么就返回其父母节点，而这个父母节点正好是LCA，为什么呢？因为这个是逐层递归上去的算法，只有在u和v的分叉节点能找到两个非零返回值，其他情况都只能找到一个或者0个非零返回值。巧妙地利用了递归的特点，把LCA作为了最终的返回值。

因为最坏情况需要递归整棵树，故此这个算法的时间效率其实是O(n)，n为整棵树的节点数。故此本算法虽然AC了，但是其实时间效率还是蛮低的。

之前分析说是O(lgn)是不对的，不好意思，如果误导了某些读者，那么表示抱歉。还好下面算法是没错的。

本算法对递归的理解还是要求挺高的，对于初学者还是有点难度。

int const MAX_N = 10001;

struct Node
{
	bool notRoot;
	vector<int> children;
};

Node Tree[MAX_N];
int N;

int find(int r, int lNode, int rNode)
{
	if (!r) return 0;
	if (r == lNode) return r;
	if (r == rNode) return r;

	vector<int> found;
	for (int i = 0; i < (int)Tree[r].children.size(); i++)
	{
		found.push_back(find(Tree[r].children[i], lNode, rNode));
	}
	int u = 0, v = 0;
	for (int i = 0; i < (int)found.size(); i++)
	{
		if (found[i] != 0)
		{
			if (u) v = found[i];
			else u = found[i];
		}
	}
	if (v) return r;
	return u;
}

void solve()
{
	scanf("%d", &N);
	memset(Tree, 0, sizeof(Tree));

	int u, v;
	for (int i = 1; i < N; i++)
	{
		scanf("%d %d", &u, &v);
		Tree[u].children.push_back(v);
		Tree[v].notRoot = 1;
	}
	int root = 0;
	for (int i = 1; i <= N; i++)
	{
		if (!Tree[i].notRoot)
		{
			root = i;
			break;
		}
	}

	scanf("%d %d", &u, &v);
	int r = find(root, u, v);
	printf("%d\n", r);//if (lin && rin) 必然是存在点，故此无需判断
}

int main()
{
	int T;
	scanf("%d", &T);
	while (T--)
	{
		solve();
	}
	return 0;
}

下面是Tarjan离线算法，效率应该和上面是一样的，多次查询的时候就能提高效率。不过实际运行比上面快。

#include <stdio.h>
#include <string.h>
#include <vector>
using std::vector;
int const MAX_N = 10001;

struct Node
{
	bool notRoot;
	bool vis;
	vector<int> children;
};

Node Tree[MAX_N];
int N;
int u, v;
int parent[MAX_N];

inline int find(int x)
{
	if (!parent[x]) return x;
	return parent[x] = find(parent[x]);
}

inline void unionTwo(int p, int x)
{
	p = find(p);
	x = find(x);
	if (p == x) return ;
	parent[x] = p;
}

bool LCATarjan(int root)
{
	Tree[root].vis = true;
	if (root == u && Tree[v].vis == true)
	{
		printf("%d\n", find(v));
		return true;
	}
	if (root == v && Tree[u].vis == true)
	{
		printf("%d\n", find(u));
		return true;
	}	
	for (int i = 0; i < (int)Tree[root].children.size(); i++)
	{
		if (LCATarjan(Tree[root].children[i])) return true;
		unionTwo(root, Tree[root].children[i]);
	}
	return false;
}

void solve()
{
	scanf("%d", &N);
	memset(Tree, 0, sizeof(Tree));
	memset(parent, 0, sizeof(parent));

	for (int i = 1; i < N; i++)
	{
		scanf("%d %d", &u, &v);
		Tree[u].children.push_back(v);
		Tree[v].notRoot = 1;
	}
	int root = 0;
	for (int i = 1; i <= N; i++)
	{
		if (!Tree[i].notRoot)
		{
			root = i;
			break;
		}
	}
	scanf("%d %d", &u, &v);
	LCATarjan(root);
}

int main()
{
	int T;
	scanf("%d", &T);
	while (T--)
	{
		solve();
	}
	return 0;
}