时间:2017/1/26 大三上学年寒假
每次寒假都挺闲的,恰好最近家里网又不太稳定,不能LOL!于是想趁这个机会,利用OpenGL,尝试着写一个仿造的《Minecraft》。但是,思来想去发现Minecraft的地形生成算法实在难以下手,因为地形需要具有:随机但又连续、复杂但又自然的效果。
凑巧在github上偶尔看到一个项目,一个大神写的minecraft,做的非常非常好。然后在他的说明文档里,注意到这个算法PerlinNoise。于是,决定写几篇博客,来总结一下关于PerlinNoise的知识。
这里也附上我使用Qt+OpenGL实现的minecraft的结果。
相关文章:
[1]博客 - [数学][转载]柏林噪声 :http://www.cnblogs.com/Memo/archive/2008/09/08/1286963.html
[2]gitbub - A simple Minecraft clone written in C using modern OpenGL (shaders). https://github.com/fogleman/Craft
[3] 我的另一篇博客《我的世界minecraft》:http://blog.csdn.net/mahabharata_/article/details/55505403
我实现的《myMinecraft》的截图:
我实现的Minecraft演示程序的下载链接:
http://download.csdn.net/detail/mahabharata_/9756981
下面这个PerlinNoise演示程序的下载链接,大家可以自己调整参数来设计自己的柏林噪声~~~
http://download.csdn.net/detail/mahabharata_/9800578
柏林噪声Perlin Noise:
关于柏林噪声的原理和算法在参考文献[1]的博客中,已经描述的非常详细。我在阅读Perlin的论文和其它博客后,先写了一个一维PerlinNoise的演示程序~。在写完这个演示程序之后,发现原来不懂的东西,现在变得直观多了!!下面写一下在演示程序中,总结的一些柏林噪声的规律。
首先上一下PerlinNoise演示程序的截图~(很简陋,一晚上写的),大家可以自己下载下来这个程序去简单模拟一下~
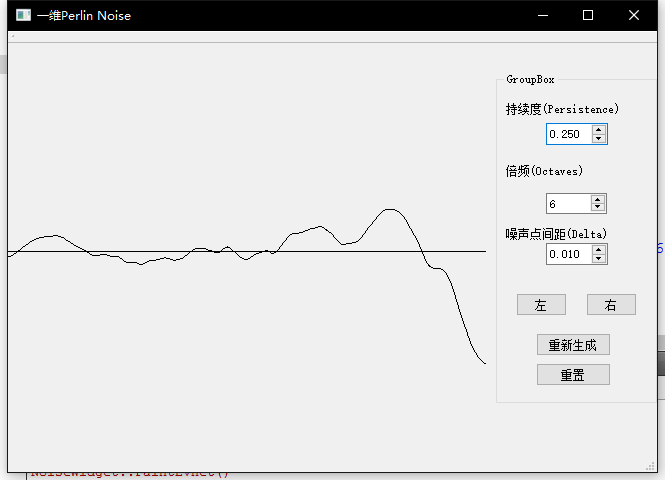
1. 持续度Persistence [ float ]:我设定的范围是(0,1]。
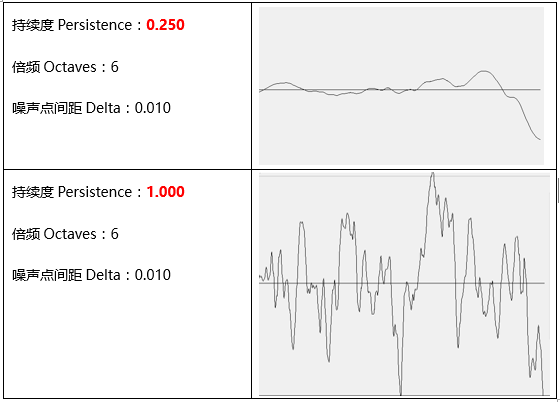
持续度越大,频率frequency越大,振幅amplitude也越大(反应在图像上,直观的表现为:波动更剧烈,更尖锐)。
2. 倍频Octaves [ int ]:我设定的范围是[0,99]
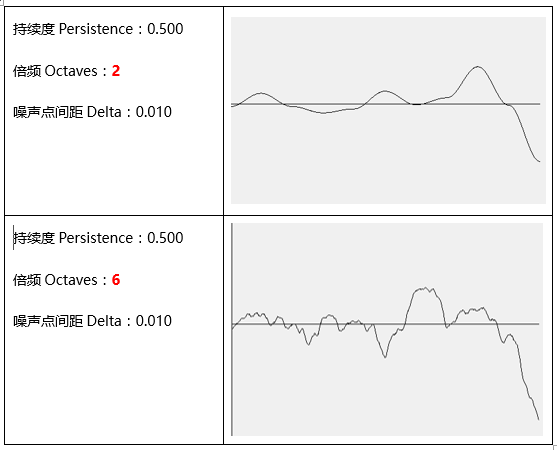
倍频越大,频率和振幅也有所增加(图像波动变大)
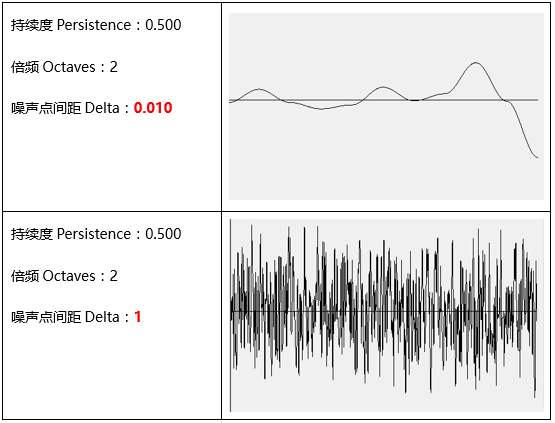
3. 噪声点间距Delta [ float ],在文章中没说到的一个值,简单的说就相当于我们数学求导中的dx,在这里相邻噪声数据的间隔。我第一次设定为1,显然生成的噪声波动很剧烈。之后较多采用的一个值是0.001,产生的数据就规律多了~上图说话!
上面Perlin Noise演示程序采用的柏林噪声的2D版([x,y]->z):
float persistence = 0.50;
int Number_Of_Octaves = 4;
double Noise(int x,int y) // 根据(x,y)获取一个初步噪声值
{
int n = x + y * 57;
n = (n<<13) ^ n;
return ( 1.0 - ( (n * (n * n * 15731 + 789221) + 1376312589) & 0x7fffffff) / 1073741824.0);
}
double SmoothedNoise(int x, int y) //光滑噪声
{
double corners = ( Noise(x-1, y-1)+Noise(x+1, y-1)+Noise(x-1, y+1)+Noise(x+1, y+1) ) / 16;
double sides = ( Noise(x-1, y) +Noise(x+1, y) +Noise(x, y-1) +Noise(x, y+1) ) / 8;
double center = Noise(x, y) / 4;
return corners + sides + center;
}
double Cosine_Interpolate(double a,double b, double x) // 余弦插值
{
double ft = x * 3.1415927;
double f = (1 - cos(ft)) * 0.5;
return a*(1-f) + b*f;
}
double InterpolatedNoise(float x,float y) // 获取插值噪声
{
int integer_X = int(x);
float fractional_X = x - integer_X;
int integer_Y = int(y);
float fractional_Y = y - integer_Y;
double v1 = SmoothedNoise(integer_X, integer_Y);
double v2 = SmoothedNoise(integer_X + 1, integer_Y);
double v3 = SmoothedNoise(integer_X, integer_Y + 1);
double v4 = SmoothedNoise(integer_X + 1, integer_Y + 1);
double i1 = Cosine_Interpolate(v1, v2, fractional_X);
double i2 = Cosine_Interpolate(v3, v4, fractional_X);
return Cosine_Interpolate(i1, i2, fractional_Y);
}
double PerlinNoise(float x,float y) // 最终调用:根据(x,y)获得其对应的PerlinNoise值
{
double total = 0;
double p = persistence;
int n = Number_Of_Octaves;
for(int i=0; i<n; i++)
{
double frequency = pow(2,i);
double amplitude = pow(p,i);
total = total + InterpolatedNoise(x * frequency, y * frequency) * amplitude;
}
return total;
}





























 731
731

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








