欧几里得几何
apk下载:https://blog.csdn.net/nameofcsdn/article/details/119086279

这是一个尺规作图的游戏。
目录:

教程:


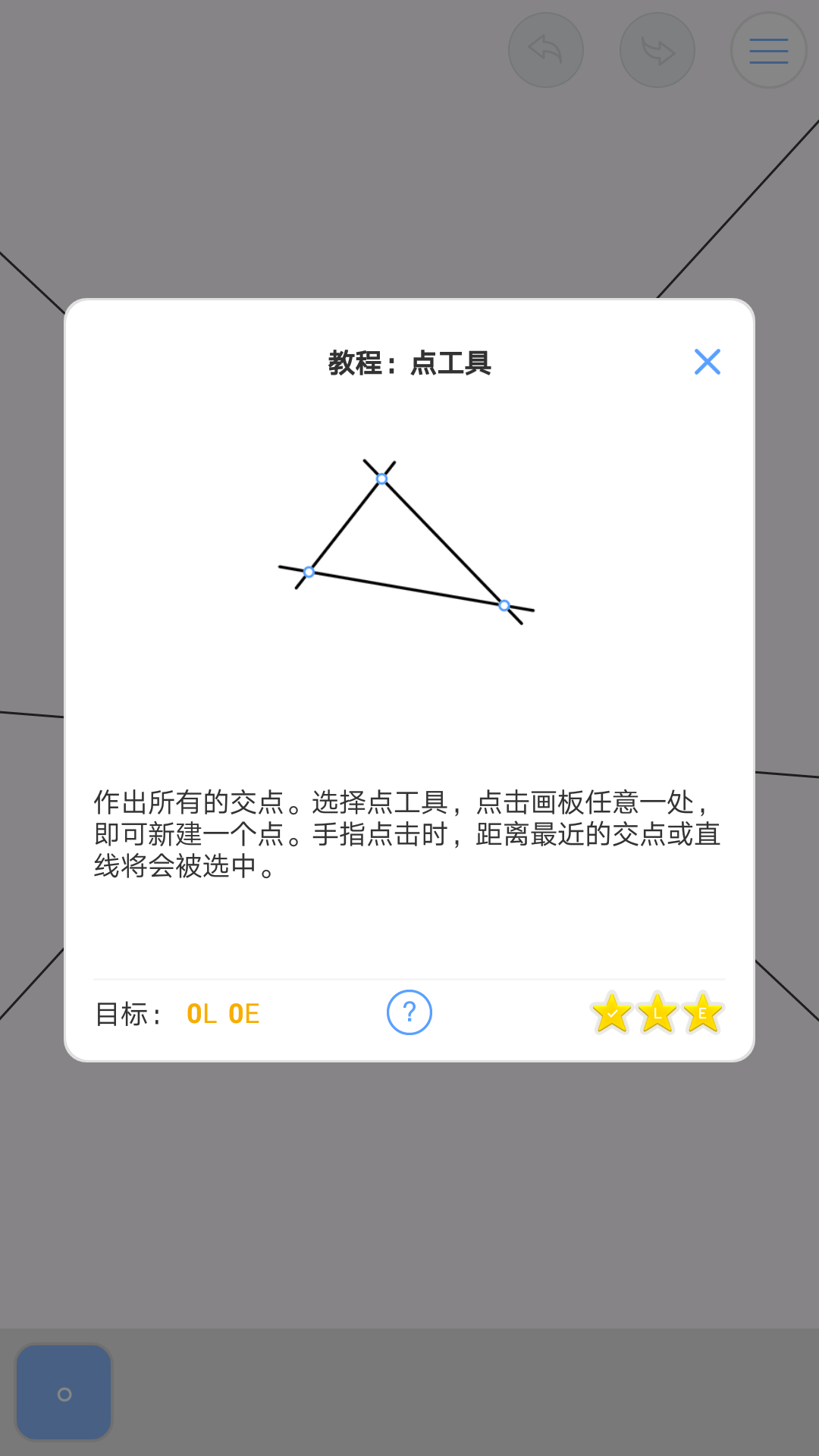




(1)



(2)


(教程)

(3)


(4)


(5)



(6)



(7)



 这是一个基于尺规作图的欧几里得几何游戏应用,包含多个版本如Alpha至Theta等。通过不同的教程帮助玩家理解并掌握欧几里得几何的基本原理及解题技巧。
这是一个基于尺规作图的欧几里得几何游戏应用,包含多个版本如Alpha至Theta等。通过不同的教程帮助玩家理解并掌握欧几里得几何的基本原理及解题技巧。
欧几里得几何
apk下载:https://blog.csdn.net/nameofcsdn/article/details/119086279

这是一个尺规作图的游戏。
目录:

教程:







(1)



(2)


(教程)

(3)


(4)


(5)



(6)



(7)



 2757
2757
 3256
3256
 1613
1613
 2255
2255

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


