集成方法：渐进梯度回归树GBRT（迭代决策树）

最新推荐文章于 2024-08-16 22:44:00 发布

-柚子皮-

最新推荐文章于 2024-08-16 22:44:00 发布

阅读量2.7w

点赞数 21

分类专栏：分类 Classification 文章标签： GBRT 迭代决策树渐进梯度回归树集成方法

本文链接：https://blog.csdn.net/pipisorry/article/details/60776803

版权

分类 Classification 专栏收录该内容

13 篇文章 5 订阅

订阅专栏

http://blog.csdn.net/pipisorry/article/details/60776803

单决策树C4.5由于功能太简单，并且非常容易出现过拟合的现象，于是引申出了许多变种决策树，就是将单决策树进行模型组合，形成多决策树，比较典型的就是迭代决策树GBRT和随机森林RF。在最近几年的paper上，如iccv这种重量级会议，iccv 09年的里面有不少文章都是与Boosting和随机森林相关的。模型组合+决策树相关算法有两种比较基本的形式：随机森林RF与GBDT，其他比较新的模型组合+决策树算法都是来自这两种算法的延伸。首先说明一下，GBRT这个算法有很多名字，但都是同一个算法：GBRT (Gradient BoostRegression Tree) 渐进梯度回归树，GBDT (Gradient BoostDecision Tree) 渐进梯度决策树，MART (MultipleAdditive Regression Tree) 多决策回归树，Tree Net决策树网络。

GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力（generalization)较强的算法。近些年更因为被用于搜索排序的机器学习模型而引起大家关注。GBRT是回归树，不是分类树（尽管GBDT调整后也可用于分类但不代表GBDT的树是分类树）。其核心就在于，每一棵树是从之前所有树的残差中来学习的。为了防止过拟合，和Adaboosting一样，也加入了boosting这一项。

GBDT主要由三个概念组成：Regression Decistion Tree（即DT)，Gradient Boosting（即GB)，Shrinkage (算法的一个重要演进分枝，目前大部分源码都按该版本实现）。搞定这三个概念后就能明白GBDT是如何工作的，要继续理解它如何用于搜索排序则需要额外理解RankNet概念。

Gradient Tree Boosting或Gradient Boosted Regression Trees（GBRT)是一个boosting的泛化表示，它使用了不同的loss函数。GBRT是精确、现成的过程，用于解决回归/分类问题。Gradient Tree Boosting模型则用于许多不同的领域：比如：网页搜索Ranking、ecology等。

GBRT优缺点

GBRT的优点是：
    天然就可处理不同类型的数据（=各种各样的features）
    预测能力强
    对空间外的异常点处理很健壮（通过健壮的loss函数）
GBRT的缺点是：
    扩展性不好，因为boosting天然就是顺序执行的，很难并行化

回归树是如何工作的？

我们以对人的性别判别/年龄预测为例来说明，每个instance都是一个我们已知性别/年龄的人，而feature则包括这个人上网的时长、上网的时段、网购所花的金额等。
分类树，我们知道C4.5分类树在每次分枝时，是穷举每一个feature的每一个阈值，找到使得按照feature<=阈值，和feature>阈值分成的两个分枝的熵最大的feature和阈值（熵最大的概念可理解成尽可能每个分枝的男女比例都远离1:1），按照该标准分枝得到两个新节点，用同样方法继续分枝直到所有人都被分入性别唯一的叶子节点，或达到预设的终止条件，若最终叶子节点中的性别不唯一，则以多数人的性别作为该叶子节点的性别。
回归树总体流程类似，不过在每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平均值{Note: 分裂点最优值是分裂点所有x对应y值的均值c，因内部最小平方误差最小[统计学习方法 5.5CART算法]}。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差--即（每个人的年龄-预测年龄）^2 的总和 / N，或者说是每个人的预测误差平方和除以 N。这很好理解，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。分枝直到每个叶子节点上人的年龄都唯一（这太难了）或者达到预设的终止条件（如叶子个数上限），若最终叶子节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。

[统计学习方法 5.5CART算法]

算法原理

不是每棵树独立训练

Boosting，迭代，即通过迭代多棵树来共同决策。这怎么实现呢？难道是每棵树独立训练一遍，比如A这个人，第一棵树认为是10岁，第二棵树认为是0岁，第三棵树认为是20岁，我们就取平均值10岁做最终结论？--当然不是！且不说这是投票方法并不是GBDT，只要训练集不变，独立训练三次的三棵树必定完全相同，这样做完全没有意义。之前说过，GBDT是把所有树的结论累加起来做最终结论的，所以可以想到每棵树的结论并不是年龄本身，而是年龄的一个累加量。

GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。这就是Gradient Boosting在GBDT中的意义。

残差提升

算法流程解释1

0.给定一个初始值

1.建立M棵决策树（迭代M次）{Note: 每次迭代生成一棵决策树}

2.对函数估计值F(x)进行Logistic变换（Note:只是归一化而已）

3.对于K各分类进行下面的操作（其实这个for循环也可以理解为向量的操作，每个样本点xi都对应了K种可能的分类yi，所以yi，F(xi)，p(xi)都是一个K维向量）

4.求得残差减少的梯度方向

5.根据每个样本点x，与其残差减少的梯度方向，得到一棵由J个叶子节点组成的决策树

6.当决策树建立完成后，通过这个公式，可以得到每个叶子节点的增益（这个增益在预测时候用的）

每个增益的组成其实也是一个K维向量，表示如果在决策树预测的过程中，如果某个样本点掉入了这个叶子节点，则其对应的K个分类的值是多少。比如GBDT得到了三棵决策树，一个样本点在预测的时候，也会掉入3个叶子节点上，其增益分别为（假设为3分类问题）：

(0.5, 0.8, 0.1), (0.2, 0.6, 0.3), (0.4, .0.3, 0.3)，那么这样最终得到的分类为第二个，因为选择分类2的决策树是最多的。

7.将当前得到的决策树与之前的那些决策树合并起来，作为一个新的模型（跟6中的例子差不多）

算法流程解释2

梯度提升

不同于前面的残差提升算法，这里使用loss函数的梯度近似残差（对于平方loss其实就是残差，一般loss函数就是残差的近似）。解决残差计算困难问题。

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

GBRT示例1（残差）

年龄预测，简单起见训练集只有4个人，A,B,C,D，他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生；C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练，会得到如下图1所示结果：

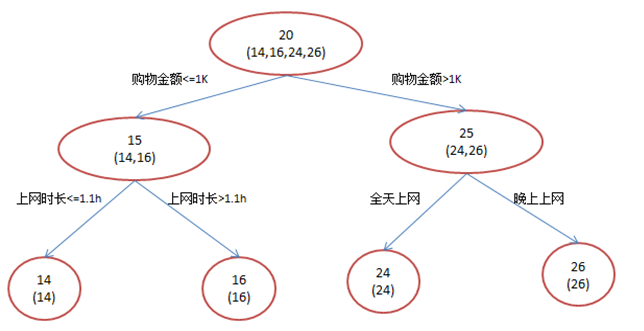
现在我们使用GBDT来做这件事，由于数据太少，我们限定叶子节点做多有两个，即每棵树只有一个分枝，并且限定只学两棵树。我们会得到如下图2所示结果：

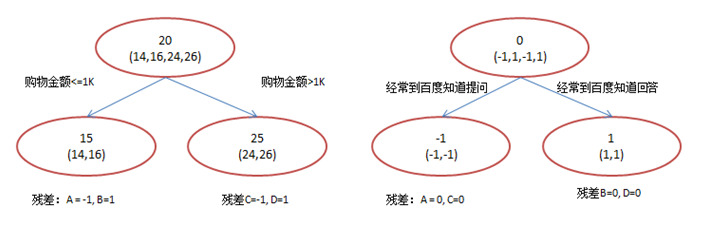
在第一棵树分枝和图1一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。此时计算残差（残差的意思就是： A的预测值 + A的残差 = A的实际值），所以A的残差就是16-15=1（注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值）。进而得到A,B,C,D的残差分别为-1,1，-1,1。然后我们拿残差替代A,B,C,D的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。换句话说，现在A,B,C,D的预测值都和真实年龄一致了。

A: 14岁高一学生，购物较少，经常问学长问题；预测年龄A = 15 – 1 = 14

B: 16岁高三学生；购物较少，经常被学弟问问题；预测年龄B = 15 + 1 = 16

C: 24岁应届毕业生；购物较多，经常问师兄问题；预测年龄C = 25 – 1 = 24

D: 26岁工作两年员工；购物较多，经常被师弟问问题；预测年龄D = 25 + 1 = 26

问题

1）既然图1和图2 最终效果相同，为何还需要GBDT呢？
    答案是过拟合。过拟合是指为了让训练集精度更高，学到了很多”仅在训练集上成立的规律“，导致换一个数据集当前规律就不适用了。其实只要允许一棵树的叶子节点足够多，训练集总是能训练到100%准确率的（大不了最后一个叶子上只有一个instance)。在训练精度和实际精度（或测试精度）之间，后者才是我们想要真正得到的。
    我们发现图1为了达到100%精度使用了3个feature（上网时长、时段、网购金额），其中分枝“上网时长>1.1h” 很显然已经过拟合了，这个数据集上A,B也许恰好A每天上网1.09h, B上网1.05小时，但用上网时间是不是>1.1小时来判断所有人的年龄很显然是有悖常识的；
    相对来说图2的boosting虽然用了两棵树，但其实只用了2个feature就搞定了，后一个feature是问答比例，显然图2的依据更靠谱。（当然，这里是故意做的数据，所以才能靠谱得如此） Boosting的最大好处在于，每一步的残差计算其实变相地增大了分错instance的权重，而已经分对的instance则都趋向于0。这样后面的树就能越来越专注那些前面被分错的instance。就像我们做互联网，总是先解决60%用户的需求凑合着，再解决35%用户的需求，最后才关注那5%人的需求，这样就能逐渐把产品做好，因为不同类型用户需求可能完全不同，需要分别独立分析。
2）Gradient呢？不是“G”BDT么？
到目前为止，我们的确没有用到求导的Gradient。在当前版本GBDT描述中，的确没有用到Gradient，该版本用残差作为全局最优的绝对方向（lz可能不知道具体步长吧？），并不需要Gradient求解。

那么哪里体现了Gradient呢？其实回到第一棵树结束时想一想，无论此时的cost function是什么，是均方差还是均差，只要它以误差作为衡量标准，残差向量(-1, 1, -1, 1)都是它的全局最优方向，这就是Gradient。

lz补充一句，均方差的梯度不就是残差吗，这就是梯度！（其它的loss函数就不一定了，但是残差向量总是全局最优的，梯度一般都是残差的近似）

3）这是boosting？Adaboost？
这是boosting，但不是Adaboost。GBDT不是Adaboost Decistion Tree。就像提到决策树大家会想起C4.5，提到boost多数人也会想到Adaboost。Adaboost是另一种boost方法，它按分类对错，分配不同的weight，计算cost function时使用这些weight，从而让“错分的样本权重越来越大，使它们更被重视”。Bootstrap也有类似思想，它在每一步迭代时不改变模型本身，也不计算残差，而是从N个instance训练集中按一定概率重新抽取N个instance出来（单个instance可以被重复sample），对着这N个新的instance再训练一轮。由于数据集变了迭代模型训练结果也不一样，而一个instance被前面分错的越厉害，它的概率就被设的越高，这样就能同样达到逐步关注被分错的instance，逐步完善的效果。Adaboost的方法被实践证明是一种很好的防止过拟合的方法，但至于为什么至今没从理论上被证明。GBDT也可以在使用残差的同时引入Bootstrap re-sampling，GBDT多数实现版本中也增加的这个选项，但是否一定使用则有不同看法。re-sampling一个缺点是它的随机性，即同样的数据集合训练两遍结果是不一样的，也就是模型不可稳定复现，这对评估是很大挑战，比如很难说一个模型变好是因为你选用了更好的feature，还是由于这次sample的随机因素。

GBRT示例2（残差）

选取回归树的分界点建立回归树

使用残差继续训练新的回归树

GBRT适用范围

该版本的GBRT几乎可用于所有的回归问题（线性/非线性），相对logistic regression仅能用于线性回归，GBRT的适用面非常广。亦可用于二分类问题（设定阈值，大于阈值为正例，反之为负例）。

搜索引擎排序应用RankNet

        搜索排序关注各个doc的顺序而不是绝对值，所以需要一个新的cost function，而RankNet基本就是在定义这个cost function，它可以兼容不同的算法（GBDT、神经网络...）。
        实际的搜索排序使用的是Lambda MART算法，必须指出的是由于这里要使用排序需要的cost function，LambdaMART迭代用的并不是残差。Lambda在这里充当替代残差的计算方法，它使用了一种类似Gradient*步长模拟残差的方法。这里的MART在求解方法上和之前说的残差略有不同，其区别描述见这里。
         搜索排序也需要训练集，但多数用人工标注实现，即对每个(query, doc)pair给定一个分值（如1, 2, 3, 4），分值越高越相关，越应该排到前面。RankNet就是基于此制定了一个学习误差衡量方法，即cost function。RankNet对任意两个文档A,B，通过它们的人工标注分差，用sigmoid函数估计两者顺序和逆序的概率P1。然后同理用机器学习到的分差计算概率P2（sigmoid的好处在于它允许机器学习得到的分值是任意实数值，只要它们的分差和标准分的分差一致，P2就趋近于P1）。这时利用P1和P2求的两者的交叉熵，该交叉熵就是cost function。
        有了cost function，可以求导求Gradient，Gradient即每个文档得分的一个下降方向组成的N维向量，N为文档个数（应该说是query-doc pair个数）。这里仅仅是把”求残差“的逻辑替换为”求梯度“。每个样本通过Shrinkage累加都会得到一个最终得分，直接按分数从大到小排序就可以了。

[【机器学习】迭代决策树GBRT（渐进梯度回归树）]

皮皮blog

python sklearn实现

分类

sklearn.ensemble.GradientBoostingClassifier(loss='deviance', learning_rate=0.1, n_estimators=100, subsample=1.0, criterion='friedman_mse', min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_split=1e-07, init=None, random_state=None, max_features=None, verbose=0, max_leaf_nodes=None, warm_start=False, presort='auto')

超过2个分类时，需要在每次迭代时引入n_classes的回归树，因此，总的索引树为（n_classes * n_estimators）。对于分类数目很多的情况，强烈推荐你使用 RandomForestClassifier 来替代GradientBoostingClassifier

回归

sklearn.ensemble.GradientBoostingRegressor(loss='ls', learning_rate=0.1, n_estimators=100, subsample=1.0, criterion='friedman_mse', min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_split=1e-07, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False, presort='auto')

参数：

n_estimators : int (default=100) 迭代次数，也就是弱学习器的个数

The number of boosting stages to perform. Gradient boostingis fairly robust to over-fitting so a large number usuallyresults in better performance.

The plot on the left shows the train and test error at each iteration.The train error at each iteration is stored in thetrain_score_ attributeof the gradient boosting model. The test error at each iterations can be obtainedvia the staged_predict method which returns agenerator that yields the predictions at each stage. Plots like these can be usedto determine the optimal number of trees (i.e. n_estimators) by early stopping.

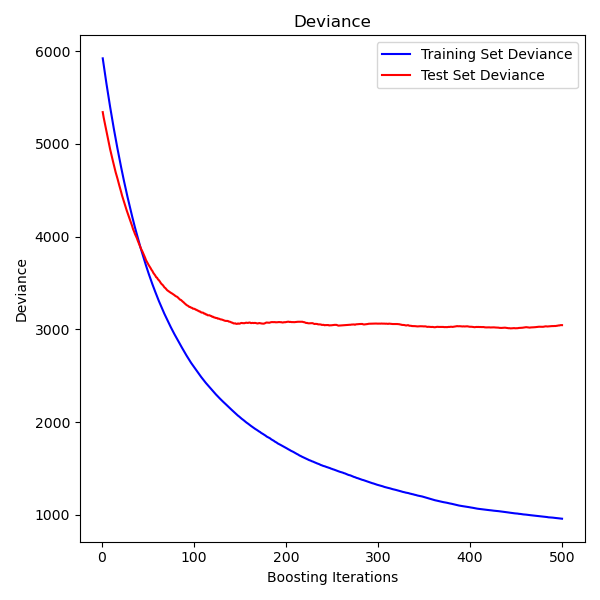
../../_images/sphx_glr_plot_gradient_boosting_regression_001.png

控制树的size

回归树的基础学习器（base learners）的size，定义了可以被GB模型捕获的各种交互的level。通常，一棵树的深度为h，可以捕获h阶的影响因子(interactions)。控制各个回归树的size有两种方法。
1 指定max_depth=h，那么将会长成深度为h的完整二元树。这样的树至多有2^h个叶子，以及2^h-1中间节点。
2 另一种方法：你可以通过指定叶子节点的数目（max_leaf_nodes）来控制树的size。这种情况下，树将使用最优搜索(best-first search)的方式生成，并以最高不纯度（impurity）的方式展开。如果树的max_leaf_nodes=k，表示具有k-1个分割节点，可以建模最高(max_leaf_nodes-1)阶的interactions。

我们发现，max_leaf_nodes=k 与 max_depth=k-1 进行比较，训练会更快，只会增大一点点的训练误差（training error）。参数max_leaf_nodes对应于gradient boosting中的变量J，与R提供的gbm包的参数interaction.depth相关，为：max_leaf_nodes == interaction.depth + 1。

数学公式Mathematical formulation

GBRT considers additive models of the following form:

$F(x) = \sum_{m=1}^{M} \gamma_m h_m(x)$

where $h_m(x)$ are the basis functions which are usually called weak learners in the context of boosting. Gradient Tree Boosting uses decision trees of fixed size as weak learners. Decision trees have a number of abilities that make them valuable for boosting, namely the ability to handle data of mixed type and the ability to model complex functions.

Similar to other boosting algorithms GBRT builds the additive model in a forward stage wise fashion: 前向分步算法

$F_m(x) = F_{m-1}(x) + \gamma_m h_m(x)$

At each stage the decision tree $h_m(x)$ is chosen to minimize the loss function $L$ given the current model $F_{m-1}$ and its fit $F_{m-1}(x_i)$

$F_m(x) = F_{m-1}(x) + \arg\min_{h} \sum_{i=1}^{n} L(y_i,F_{m-1}(x_i) - h(x))$

Note: 应该是F_{m-1}(x_i) + h(x)吧，残差为yi - (F_{m-1}(x_i) + h(x))训练下一个回归树

The initial model $F_{0}$ is problem specific, for least-squares regression one usually chooses the mean of the target values.

Note:

The initial model can also be specified via the init argument. The passed object has to implement fit and predict.

Gradient Boosting attempts to solve this minimization problem numerically via steepest descent: The steepest descent direction is the negative gradient of the loss function evaluated at the current model $F_{m-1}$ which can be calculated for any differentiable loss function:

$F_m(x) = F_{m-1}(x) + \gamma_m \sum_{i=1}^{n} \nabla_F L(y_i,F_{m-1}(x_i))$ Note: 这里使用的是残差的近似--梯度来计算残差的。

Where the step length $\gamma_m$ is chosen using line search:

$\gamma_m = \arg\min_{\gamma} \sum_{i=1}^{n} L(y_i, F_{m-1}(x_i)- \gamma \frac{\partial L(y_i, F_{m-1}(x_i))}{\partial F_{m-1}(x_i)})$

The algorithms for regression and classification only differ in the concrete loss function used.

loss函数

回归

最小二乘法Least squares（’ls’）：最自然的选择，因为它的计算很简单。初始模型通过target的平均值来给出。
最小绝对偏差Least absolute deviation （’lad’）：一个健壮的loss函数，用于回归。初始模型通过target的中值来给出。
Huber (‘huber’): Another robust loss function that combinesleast squares and least absolute deviation; use alpha tocontrol the sensitivity with regards to outliers (see [F2001] formore details).
Quantile (‘quantile’):A loss function for quantile regression.Use 0 < alpha < 1 to specify the quantile. This loss functioncan be used to create prediction intervals(see Prediction Intervals for Gradient Boosting Regression).

分类

Binomial deviance ('deviance'): The negative binomiallog-likelihood loss function for binary classification (providesprobability estimates). The initial model is given by thelog odds-ratio.
Multinomial deviance ('deviance'): The negative multinomiallog-likelihood loss function for multi-class classification withn_classes mutually exclusive classes. It providesprobability estimates. The initial model is given by theprior probability of each class. At each iteration n_classesregression trees have to be constructed which makes GBRT ratherinefficient for data sets with a large number of classes.
Exponential loss ('exponential'): The same loss functionas AdaBoostClassifier. Less robust to mislabeledexamples than 'deviance'; can only be used for binaryclassification.

正则化

缩减Shrinkage

Shrinkage（缩减）的思想认为，每次走一小步逐渐逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树，它认为每棵树只学到了真理的一小部分，累加的时候只累加一小部分，通过多学几棵树弥补不足。用方程来看更清晰，即
没用Shrinkage时：（yi表示第i棵树上y的预测值， y(1~i)表示前i棵树y的综合预测值）
y(i+1) = 残差(y1~yi)，其中：残差(y1~yi) = y真实值 - y(1 ~ i)
y(1 ~ i) = SUM(y1, ..., yi)

Shrinkage不改变第一个方程，只把第二个方程改为：
y(1 ~ i) = y(1 ~ i-1) + step * yi
即Shrinkage仍然以残差作为学习目标，但对于残差学习出来的结果，只累加一小部分（step*残差）逐步逼近目标，step一般都比较小，如0.01~0.001（注意该step非gradient的step），导致各个树的残差是渐变的而不是陡变的。直觉上这也很好理解，不像直接用残差一步修复误差，而是只修复一点点，其实就是把大步切成了很多小步。本质上，Shrinkage为每棵树设置了一个weight，累加时要乘以这个weight，但和Gradient并没有关系。这个weight就是step。就像Adaboost一样，Shrinkage能减少过拟合发生也是经验证明的，目前还没有看到从理论的证明。

[f2001]提出了一种简单的正则化策略，它通过一个因子v将每个弱学习器的贡献进行归一化（为什么学习率v能将每个弱学习器的贡献进行归一化？）。

$F_m(x) = F_{m-1}(x) + \nu \gamma_m h_m(x)$

参数v也被称为学习率（learning rate），因为它可以对梯度下降的步长进行调整；它可以通过learning_rate参数进行设定。

参数learning_rate会强烈影响到参数n_estimators（即弱学习器个数）。learning_rate的值越小，就需要越多的弱学习器数来维持一个恒定的训练误差(training error)常量。经验上，推荐小一点的learning_rate会对测试误差(test error)更好。[HTF2009]推荐将learning_rate设置为一个小的常数（e.g. learning_rate <= 0.1），并通过early stopping机制来选择n_estimators。我们可以在[R2007]中看到更多关于learning_rate与n_estimators的关系。

子抽样Subsampling

[F1999]提出了随机梯度boosting，它将bagging(boostrap averaging)与GradientBoost相结合。在每次迭代时，基础分类器(base classifer)都在训练数据的一个子抽样集中进行训练。子抽样以放回抽样。subsample的典型值为：0.5。

下图展示了shrinkage的效果，并在模型的拟合优度（Goodness of Fit）上进行子抽样（subsampling）。我们可以很清楚看到：shrinkage的效果比no-shrinkage的要好。

减小variance策略1：使用shrinkage的子抽样可以进一步提升模型准确率。而不带shinkage的子抽样效果差些。

../_images/sphx_glr_plot_gradient_boosting_regularization_0011.png

减小variance策略2：对features进行子抽样（类比于RandomForestClassifier中的随机split）。子抽样features的数目可以通过max_features参数进行控制。注意：使用小的max_features值可以极大地降低运行时长。

out-of-bag估计

随机梯度boosting允许计算测试偏差（test deviance）的out-of-bag估计，通过计算没有落在bootstrap样本中的其它样本的偏差改进（i.e. out-of-bag示例）。该提升存在属性oob_improvement_中。oob_improvement_[i]表示在添加第i步到当前预测中时，OOB样本中的loss的提升。OOB估计可以被用于模型选择，例如：决定最优的迭代数。OOB估计通常很少用，我们推荐你使用交叉验证（cross-validation），除非当cross-validation十分耗时的时候。

示例：[Gradient Boosting regularization; Gradient Boosting Out-of-Bag estimates; OOB Errors for Random Forests]

内省Interpretation

单颗决策树可以通过内省进行可视化树结构。然而，GradientBoost模型由成百的回归树组成，不能轻易地通过对各棵决策树进行内省来进行可视化。幸运的是，已经提出了许多技术来归纳和内省GradientBoost模型。

feature重要程度

通常，features对于target的结果预期的贡献不是均等的；在许多情况下，大多数features都是不相关的。当内省一个模型时，第一个问题通常是：在预测我们的target时，哪些features对结果预测来说是重要的。

单棵决策树天生就可以通过选择合适的split节点进行特征选择（feature selection）。该信息可以用于计算每个feature的重要性；基本思想是：如果一个feature经常用在树的split节点上，那么它就越重要。这个重要性的概率可以延伸到决策树家族ensembles方法上，通过对每棵树的feature求简单平均即可。

GradientBoosting模型的重要性分值，可以通过feature_importances_属性来访问：

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_  
array([ 0.11,  0.1 ,  0.11,  ...

示例：Gradient Boosting regression

局部依赖

局部依赖图（Partial dependence plots ：PDP）展示了target结果与一些目标特征（target feature）之间的依赖；边缘化（marginalizing）所有其它特征（’complement’ features）。另外，我们可以内省这两者的局部依赖性。

由于人的认知的有限，目标特征的size必须设置的小些（通常：1或2），目标特征可以在最重要的特征当中进行选择。

下图展示了关于California居住情况的、4个one-way和一个two-way的局部依赖图示例：

../_images/sphx_glr_plot_partial_dependence_0011.png

one-way的PDP图告诉我们，target结果与target特征之间的相互关系（e.g. 线性/非线性）。左上图展示了中等收入（median income）在房价中位数（median house price）上的分布；我们可以看到它们间存在线性关系。带有两个target特征的PDP，展示了和两个特征的相关关系。例如：上图最后一张小图中，两个变量的PDP展示了房价中位数（median house price）与房龄（house age）和平均家庭成员数（avg. occupants）间的关系。我们可以看到两个特征间的关系：对于AveOccup>2的，房价与房龄（HouseAge）几乎完全独立。而AveOccup<2的，房价则强烈依赖年齡。

partial_dependence模块

提供了一个很方便的函数：plot_partial_dependence 来创建one-way以及two-way的局部依赖图。下例，我们展示了如何创建一个PDP：两个two-way的PDP，feature为0和1，以及一个在这两个feature之间的two-way的PDP：

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.ensemble.partial_dependence import plot_partial_dependence

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> fig, axs = plot_partial_dependence(clf, X, features)

对于多分类的模块，我们需要设置类的label，通过label参数来创建PDP：

>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10, max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> fig, axs = plot_partial_dependence(mc_clf, X, features, label=0)

如果你需要一个局部依赖函数的原始值，而非你使用partial_dependence函数绘制的图：

>>> from sklearn.ensemble.partial_dependence import partial_dependence

>>> pdp, axes = partial_dependence(clf, [0], X=X)
>>> pdp  
array([[ 2.46643157,  2.46643157, ...
>>> axes  
[array([-1.62497054, -1.59201391, ...

该函数需要两个参数：

grid: 它控制着要评估的PDP的target特征的值
X: 它提供了一个很方便的模式来从训练数据集上自动创建grid。

返回值axis：

-如果给定了X，那么通过这个函数返回的axes给出了每个target特征的axis.

对于在grid上的target特征的每个值，PDP函数需要边缘化树的不重要特征的预测。在决策树中，这个函数可以用来评估有效性，不需要训练集数据。对于每个grid点，会执行一棵加权树的遍历：如果一个split节点涉及到’target’特征，那么接下去的左、右分枝，每个分枝都会通过根据进入该分枝的训练样本的fraction进行加权。最终，通过访问所有叶子的平均加权得到局部依赖。对于树的ensemble来说，每棵树的结果都会被平均。

注意点：