最小度限制生成树

设G=(V, E, ω)是连通的无向图，v0 ∈V是特别指定的一个顶点,k为给定的一个正整数。如果T是G的一个生成树且dT(v0)=k，则称T为G的k度限制生成树。G中权值和最小的k度限制生成树称为G的最小k度限制生成树

明确几个概念
T为图G的一个生成树，T+a-b记作(+a,-b)，如果T+a-b仍然是一个生成树，则称(+a,-b）是T的一个可行交换。

T为图G的一个生成树，由T进行一次可行交换得到的新的生成树所组成的集合，称为T的邻集,记为N(T)。

定 理

定理：设T是图G的最小k度限制树，E0是G中与v0有关联的边的集合，
E1=E0\E(T)，
E1即是和V0相连，但是不在T中的边的集合
E2=E(T)\E0，
E2即是T中不和V0相连的边的集合
A={(+a,-b)| a∈E1,b∈E2}
设ω(a’)－ω(b’)=min{ω(a)－ω(b)| (+a,-b)∈A}，则T + a’-b’是G的一个最小k+1度限制生成树。

即最小k+1度限制生成树属于最小k度限制生成树的邻集。

---

假设我们已经得到了最小p度限制生成树，
如何通过它来求最小p+1度限制生成树呢？

由定理可知最小p+1度限制生成树属于最小p度生成树的邻集，因此它可以通过枚举最小p度生成树上的一次可行交换求得。

为了使v0的度增加，枚举的可行交换中必须有一条边与v0关联。

如图，假设我们已经得到了v0点度为2时的最小生成树，现在要求v0度为3时的最小生成树。

我们枚举于V0关联且不在树上边，分别添加到树上，例如：

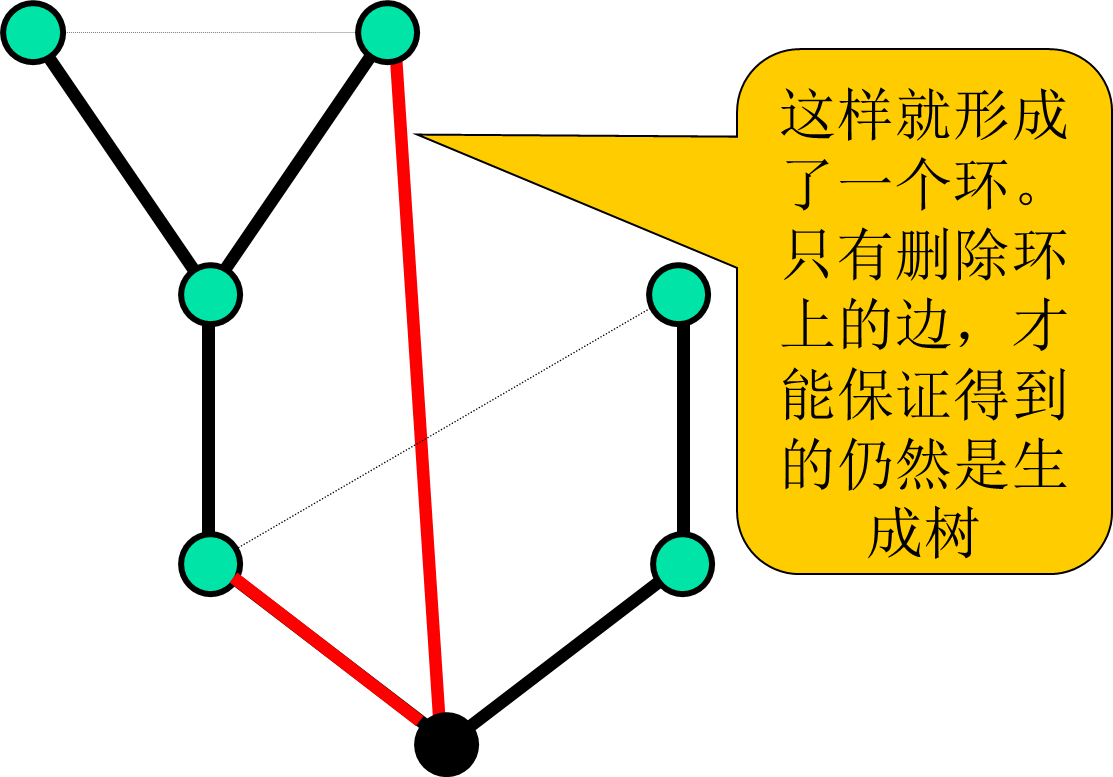
为了使V0的度增加，图中两条边红色的边是不能删除的

删去边的权值越大，所得到的生成树的权值和就越小，因此，需要找到环上可删除的权值最大的边并将其删除。

简单的枚举 但 时间复杂度非常高！！！

造成时间复杂度高的主要原因是有大量的重复计算

用动态规划可以避免大量重复计算

设最小p度限制生成树为T,T是无根树，为了简便，我们把v0作为该树的根。
定义Father(v)为T中v的父结点，Father(v0)无意义。
设Best(v)为路径v0->v上与v0无关联且权值最大的边。

Best(v)的状态转移方程为
Best(v)=max(Best(Father(v)),ω(Father(v),v))

边界条件为
Best[v0]=-∞，Best[v’]=-∞|(v0,v’)∈E(T)。
因为每次寻找的是最大边,所以-∞不会被考虑

状态总共|V|个，而状态转移的时间复杂度为O(1),因而总的时间复杂度是O(V),即通过最小p度限制生成树求最小p+1度限制生成树的时间复杂度是O(V)。

具体实现：从V0开始做一遍搜索即可。
问题：最先求几度的最小度限制生成树呢？即p从多少开始求？

因为求最小k度限制生成树，当 k < DG(v0) 时，问题并不总是有解的。如图。

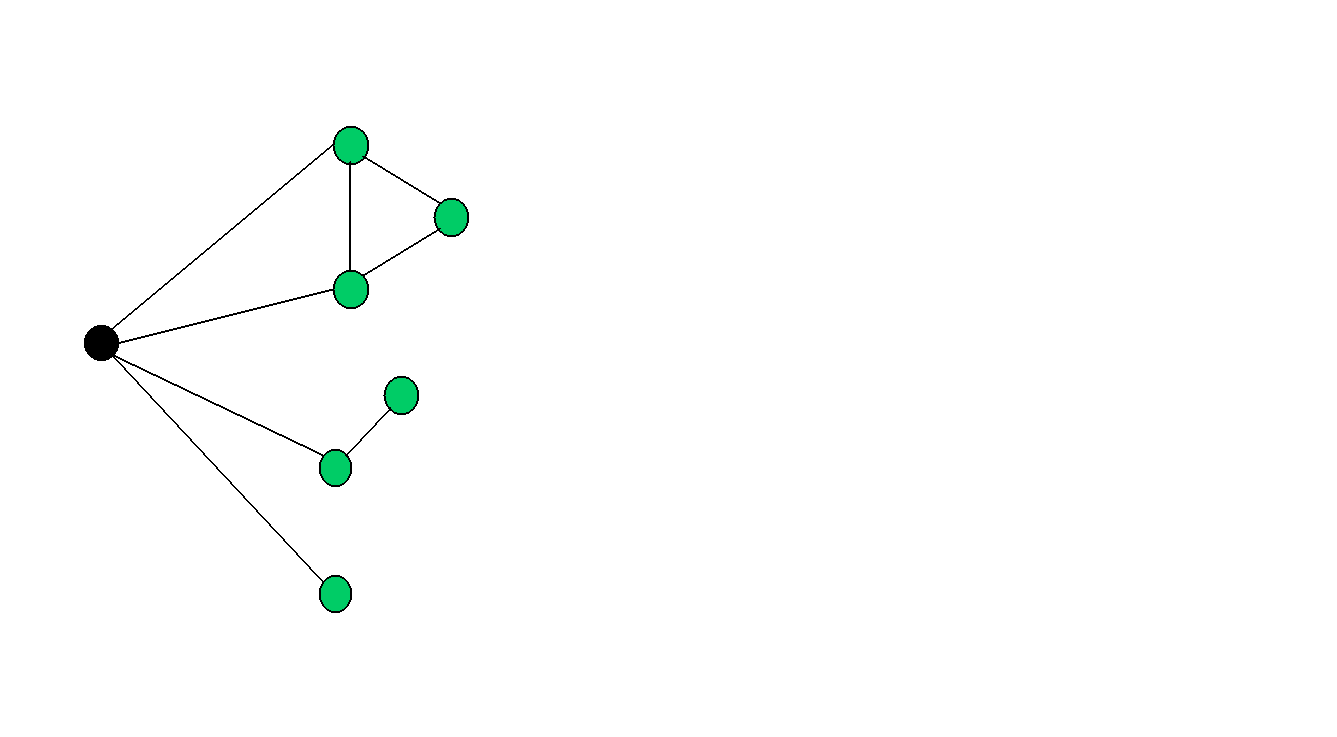
k≤2,不存在k度限制生成树

将v0从图中删去，图中将会出现3个连通分量

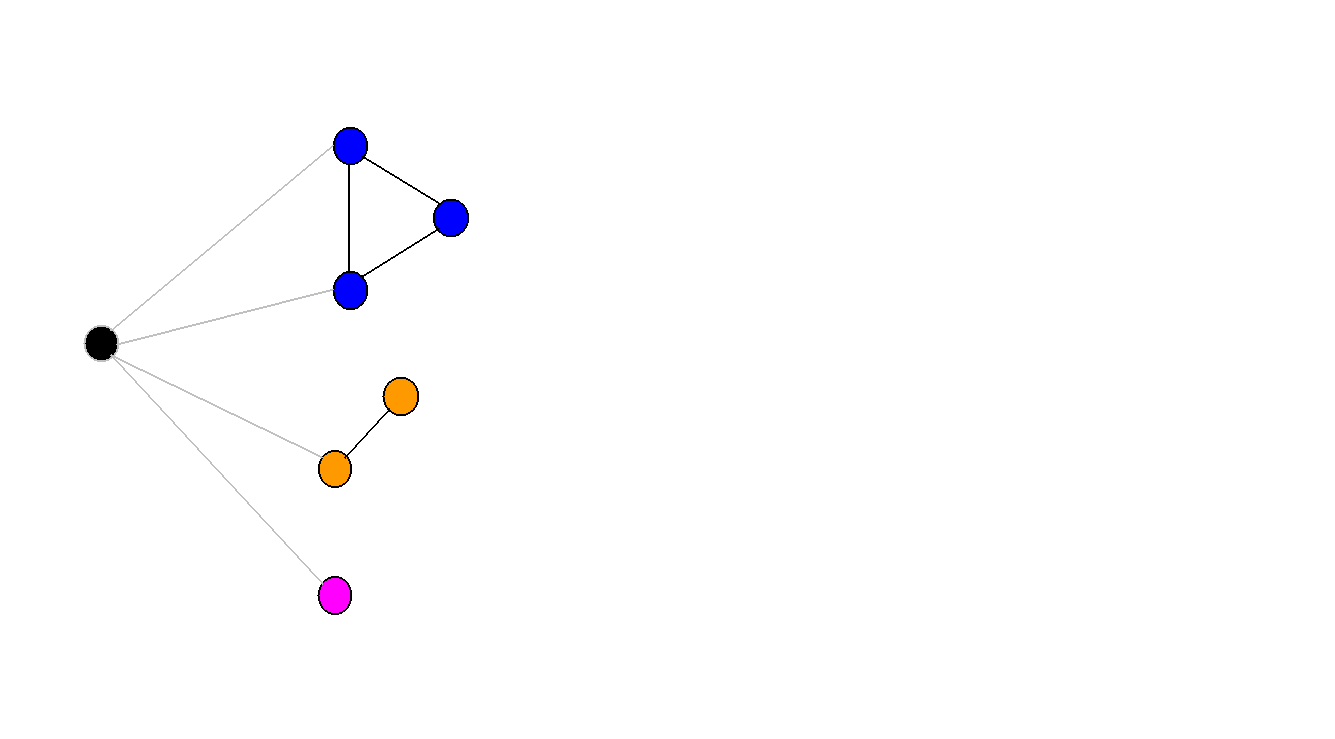
而这3个连通分量必须通过v0来连接，k<3无解

所以如果将v0去掉，图会被分成m个连通支，那么就先求最小m度限制生成树。

如何求最小m度限制生成树

1）我们可以先删去v0，对各个连通分量求最小生成树。

2）再在每个连通分量中找最小边和v0相连。

3）得到最小m度限制生成树。

时间复杂度分析

求最小m度生成树：O(VlogV+E);

最多k次从p度到p+1度的递推：k*O(V);

总复杂度：O(VlogV+E+kV);

模板题，poj1639

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <map>
#include <algorithm>
using namespace std;
const int INF = ~0u>>2;
const int N = 50;
int father[N];
int g[N][N];
bool flag[N][N];
map<string, int> num;
int n, k, cnt, ans;

struct Node{
    int x, y, v;
    friend bool operator < (Node n1, Node n2){
        return n1.v < n2.v;
    }
}a[1010];
Node dp[N];
//dp(v)为路径v0—v上与v0无关联且权值最大的边; 
int find(int x){
    if (x != father[x]){
        father[x] = find(father[x]);
    }
    return father[x];
}

void kruskal(){  
    int i;
    for (i = 1; i <= n; i++){
        if (a[i].x == 1 || a[i].y == 1) continue;
        int x = find(a[i].x);
        int y = find(a[i].y);
        if (x == y) continue;
        flag[a[i].x][a[i].y] = flag[a[i].y][a[i].x] = true;
        father[x] = y;
        ans += a[i].v;
    }
}


void dfs(int x, int pre){  //dfs求1到某节点路程上的最大值
    int i;
    for (i = 2; i <= cnt; i++){
        if (i != pre && flag[x][i]){
            if (dp[i].v == -1){
                if (dp[x].v > g[x][i]){
                    dp[i] = dp[x];
                }else{
                    dp[i].v = g[x][i];
                    dp[i].x = x;   //记录这条边
                    dp[i].y = i;
                }
            }
            dfs(i, x);
        }
    }
}

void init(){
    ans = 0;
    cnt = 1;
    memset(flag, false, sizeof(flag));
    memset(g, -1, sizeof(g));
    num["Park"] = 1;
    for (int i = 0; i < N; i++){
        father[i] = i;
    }
}
int main(){
#ifndef ONLINE_JUDGE
    freopen("1.txt", "r", stdin);
#endif
    int i, j, v;
    string s;
    scanf("%d", &n);
    init();
    for (i = 1; i <= n; i++){
        cin >> s;
        if (num.find(s) == num.end()){
            num[s] = ++cnt;
        }
        a[i].x = num[s];
        cin >> s;
        if (num.find(s) == num.end()){
            num[s] = ++cnt;
        }
        a[i].y = num[s];
        scanf("%d", &v);
        a[i].v = v;
        if (g[a[i].x][a[i].y] == -1){
            g[a[i].x][a[i].y] = g[a[i].y][a[i].x] = v;
        }else{
            g[a[i].x][a[i].y] = g[a[i].y][a[i].x] = min(v, g[a[i].x][a[i].y]);
        }
    }
    scanf("%d", &k);
    int set[N], Min[N];
    for (i = 0; i < N; i++){
        Min[i] = INF;
    }
    sort(a+1, a+n+1);
    kruskal();
    for (i = 2; i <= cnt; i++){  //寻找1到这些连通块的最小距离 
        if (g[1][i] != -1){
            int x = find(i);
            if (Min[x] > g[1][i]){
                Min[x] = g[1][i];
                set[x] = i;
            }
        }
    }
    int m = 0;
    for (i = 1; i <= cnt; i++){  //把1跟这些连通块连接起来
        if (Min[i] != INF){
            m++;
            flag[1][set[i]] = flag[set[i]][1] = true;
            ans += g[1][set[i]];
        }
    }
    for (i = m+1; i <= k; i++){
        memset(dp, -1, sizeof(dp));
        dp[1].v = -INF;
        for (j = 2; j <= cnt; j++){
            if (flag[1][j]){
                dp[j].v = -INF;
            }
        }
        dfs(1, -1);
        int tmp, Min = INF;
        for (j = 2; j <= cnt; j++){
            if (g[1][j] != -1){
                if (Min > g[1][j] - dp[j].v){ 
            //找到一条dp到连通块中某个点的边，替换原来连通块中的边
                    Min = g[1][j]-dp[j].v;
                    tmp = j;
                }
            }
        }
        int x = dp[tmp].x, y = dp[tmp].y;
        flag[1][tmp] = flag[tmp][1] = true;
        flag[x][y] = flag[y][x] = false;
        ans += Min;
    }
    cout << "Total miles driven: " << ans << endl;
    return 0; 
}

---

本文参考国家集训队论文，