B. Code For 1

B. Code For 1

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Jon fought bravely to rescue the wildlings who were attacked by the white-walkers at Hardhome. On his arrival, Sam tells him that he wants to go to Oldtown to train at the Citadel to become a maester, so he can return and take the deceased Aemon's place as maester of Castle Black. Jon agrees to Sam's proposal and Sam sets off his journey to the Citadel. However becoming a trainee at the Citadel is not a cakewalk and hence the maesters at the Citadel gave Sam a problem to test his eligibility.

Initially Sam has a list with a single element n. Then he has to perform certain operations on this list. In each operation Sam must remove any element x, such that x > 1, from the list and insert at the same position , , 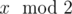 sequentially. He must continue with these operations until all the elements in the list are either 0 or 1.

Now the masters want the total number of 1s in the range l to r (1-indexed). Sam wants to become a maester but unfortunately he cannot solve this problem. Can you help Sam to pass the eligibility test?

Input

The first line contains three integers n, l, r (0 ≤ n < 250, 0 ≤ r - l ≤ 105, r ≥ 1, l ≥ 1) – initial element and the range l to r.

It is guaranteed that r is not greater than the length of the final list.

Output

Output the total number of 1s in the range l to r in the final sequence.

Examples

input

7 2 5

output

4

input

10 3 10

output

5

Note

Consider first example:

Elements on positions from 2-nd to 5-th in list is [1, 1, 1, 1]. The number of ones is 4.

For the second example:

Elements on positions from 3-rd to 10-th in list is [1, 1, 1, 0, 1, 0, 1, 0]. The number of ones is 5.

题意什么的就不用说了。

思路：

首先看一下给的区间长度是1e5.也就是说我们可以每次logn的查找到我们要找的那个数就没有问题。

首先就是看一下规律。其实这个拆分本身就是对称的。下标开始以中间为轴，每次除以2得到下一个对称轴。而当前点的值就是n&1.每次n也是除以2.关于对称是怎么看出来的，我是直接画了一棵二叉树，很容易就发现左右子树是对称的。而左子树根节点自然是2的n次方。

所以我们可以求出这些下标为1.2.4.8.....的值然后存起来。

之后在区间加和的时候，把大的下标对称到已经求出来的值中，就可以了。这样操作上每次达到logn。

#include <bits/stdc++.h>

using namespace std;
const int MAXN=1e5+7;
long long cnt;
map<long long,int>num;
void init(long long n)//求出下标为2的幂次方的那些值
{
    cnt=log2(n);
    cnt=pow(2,cnt);
    while(cnt)
    {
        num[cnt]=n&1;
        n>>=1;
        cnt>>=1;
    }
}
long long find_pos(long long pos)//对称到已经求出来的值中
{
    if(pos&1)return 1;
    long long p=2;
    while(pos%p==0)
    {
        if(pos==p)return pos;
        p<<=1;
    }
    return p>>1;
}

int main()
{
    long long n;
    long long l,r;
    scanf("%I64d%I64d%I64d",&n,&l,&r);
    init(n);
    long long ans=0;
    for(long long i=l; i<=r; ++i)
    {
        ans+=num[find_pos(i)];
    }
    printf("%I64d\n",ans);
    return 0;
}