最近开始对凸优化(convex optimization)中的ADMM(Alternating Direction Method of Multipliers)交替方向乘子算法开始感兴趣,接下来我会写一系列关于ADMM(Alternating Direction Method of Multipliers)交替方向乘子算法的内容。
凸优化:ADMM(Alternating Direction Method of Multipliers)交替方向乘子算法系列之五: Constrained Convex Optimization
本文地址:http://blog.csdn.net/shanglianlm/article/details/46807865
5- 约束凸优化(Constrained Convex Optimization)
通用的约束凸优化问题为
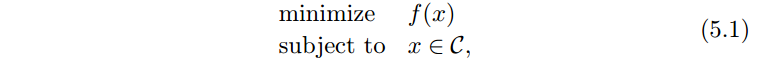
其中
x∈Rn
, f 和 C 是凸的。改写成 ADMM 形式
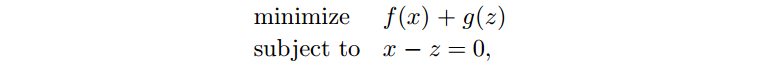
其中 g 是 C 的指示函数。增广 Lagrangian 为
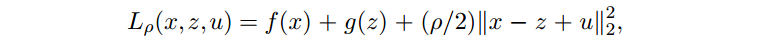
因此有
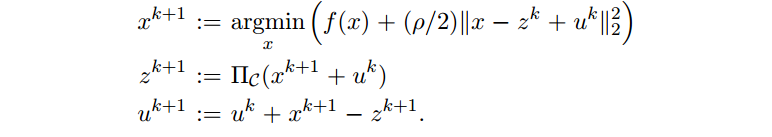
x-update 涉及最小化 f 加 一个凸二次函数;z-update 是一个 C 上的 Euclidean 映射。这里目标函数 f 不要求光滑。
As with all problems where the constraint is x − z = 0, the primal and dual residuals take the simple form
5-1 凸可行性(Convex Feasibility)
5-1-1 交替投影法(Alternating Projections)
找到两个闭合非空凸集的交集中的一个点的常用方法是 alternating projections 算法
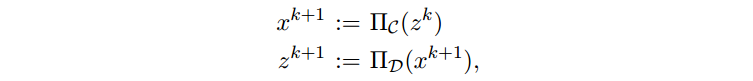
其中
ΠC
和
ΠD
分别是 集合 C 和 D 上的 Euclidean 映射。
原问题写成 ADMM 形式,
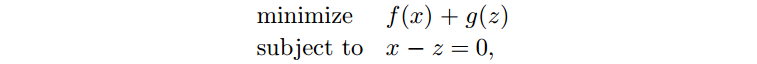
其中 f 和 g 分别是 C 和 D 的指示函数(indicator function)。
ADMM 的缩放形式(scaled form)
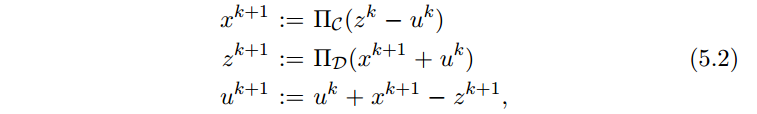
x- 和 z- 步都涉及在一个凸集上的映射。
5-1-2 平行投影法(Parallel Projections)
扩展到找到 N 个闭合凸集
A1,...,AN
交错集上的点,
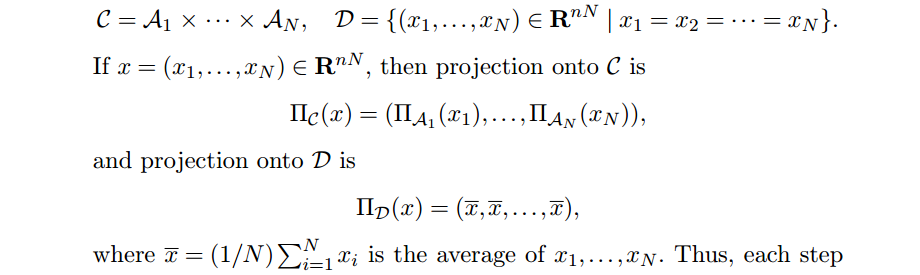
接着有
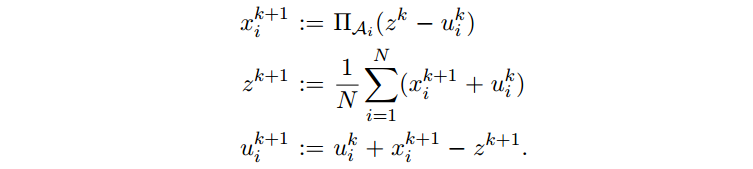
第一和三步可以并行。
5-2 线性和二次规划(Linear and Quadratic Programming)
标准的二次规划 quadratic program (QP) 形式为
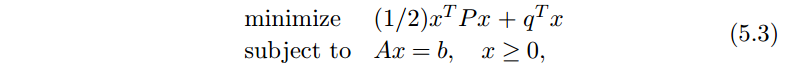
表示成 ADMM 形式
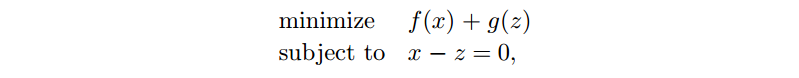
其中
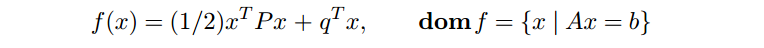
g 是非负象限
Rn+
的指示函数。
ADMM 的缩放形式(scaled form)
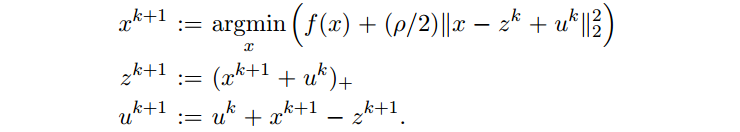
x-update 是一个有优化条件的等式约束最小二次问题(an equality-constrained least squares problem with optimality conditions)。
参考或延伸材料:
[1]Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers
[2] 凸优化讲义
[3] A Note on the Alternating Direction Method of Multipliers










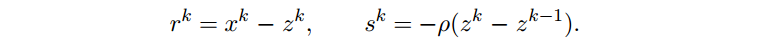

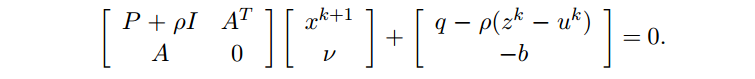















 389
389

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










