理解支持向量机（二）核函数

由之前对核函数的定义（见统计学习方法定义7.6）：
设χ是输入空间（欧氏空间或离散集合），Η为特征空间（希尔伯特空间），如果存在一个从χ到Η的映射

φ(x): χ→Η

使得对所有的x,z∈χ,函数Κ(x,z)=φ(x)∙φ(z)，
则称Κ(x,z)为核函数，φ(x)为映射函数，φ(x)∙φ(z)为x,z映射到特征空间上的内积。
由于映射函数十分复杂难以计算，在实际中，通常都是使用核函数来求解内积，计算复杂度并没有增加，映射函数仅仅作为一种逻辑映射，表征着输入空间到特征空间的映射关系。例如：
设输入空间χ： ,

映射函数φ(x)= < X,X > =
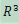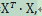
核函数Κ(x,z)=
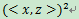
那么，取两个样例x=(1,2,3),z=(4,5,6)分别通过映射函数