支持向量机及其核函数

01_6

于 2024-07-02 22:55:56 发布

阅读量861

点赞数 26

文章标签：机器学习支持向量机算法

本文链接：https://blog.csdn.net/2301_77444219/article/details/140136244

版权

引言

在机器学习领域，支持向量机（SVM）以其出色的性能和广泛的应用而闻名。SVM是一种监督学习模型，用于分类和回归分析。它的核心优势在于其在高维空间中进行线性分割的能力，以及通过核技巧处理非线性问题的能力。本文将深入探讨SVM的基本原理和核函数的作用。

支持向量机基础

线性可分支持向量机

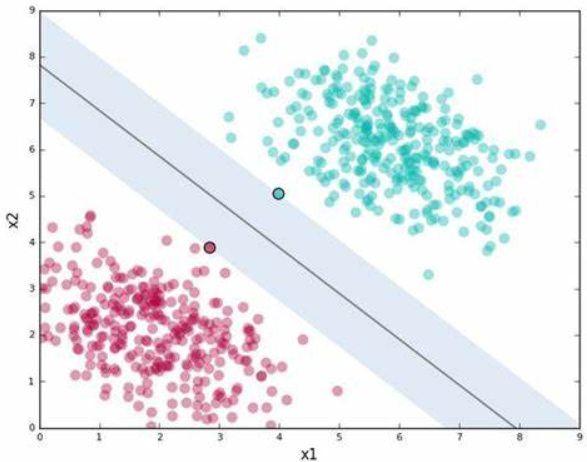
SVM的基本概念是找到数据点之间的最优边界，这个边界被称为超平面。在最简单的情况下，即数据是线性可分的，SVM的目标是找到一个超平面（淡蓝色的区域），它不仅能够正确分类数据，而且与最近的点（支持向量）之间的距离最大化（中间的实线）。

软间隔

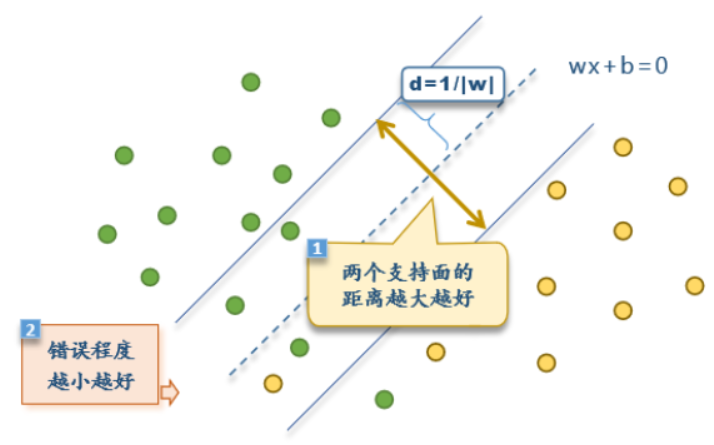
软间隔SVM允许正支持平面的负侧有正样本，也允许负支持平面正侧有负样本，它的目标在于，尽量让两个支持面的距离更大的同时。

核函数的魔力

非线性问题的处理

尽管SVM在处理线性可分数据方面表现出色，但现实世界中的数据往往是非线性的。这就是核函数发挥作用的地方。核函数允许SVM在高维空间中寻找非线性边界，而无需显式地映射输入数据到高维空间。

常见核函数

1. 线性核（Linear Kernel）

线性核是最简单的核函数，它不进行任何变换，直接使用原始特征空间。当数据在原始特征空间中线性可分时，线性核是最有效的。

公式： $K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i \cdot \mathbf{x}_j$

其中 𝑥𝑖和 𝑥𝑗是数据点在原始特征空间中的向量表示。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

# 生成或者加载一个线性可分但区分度较低的样本数据集
# 这里我们使用鸢尾花数据集的前两个特征，并进行一定的调整以接近线性可分但区分度不高的情况
iris = datasets.load_iris()
X = iris.data[:, :2]  # 取前两个特征
y = iris.target
mask = y != 2  # 仅保留前两类以便于线性可分的演示
X = X[mask]
y = y[mask]

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# 使用线性核函数的支持向量机
svm_linear = SVC(kernel='linear', C=1)
svm_linear.fit(X_train, y_train)

# 绘制原始数据分布及线性SVM的决策边界
plt.figure(figsize=(12, 6))

# 原始数据分布
plt.subplot(1, 2, 1)
plt.scatter(X_scaled[y == 0, 0], X_scaled[y == 0, 1], color='lightblue', label='Class 0')
plt.scatter(X_scaled[y == 1, 0], X_scaled[y == 1, 1], color='lightcoral', label='Class 1')
plt.title('Original Data')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()

# 计算并绘制线性超平面
xlim = plt.xlim()
ylim = plt.ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
XX, YY = np.meshgrid(xx, yy)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = svm_linear.decision_function(xy).reshape(XX.shape)
plt.contour(XX, YY, Z, colors='gray', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.xlim(xlim)
plt.ylim(ylim)

# 经过线性核函数SVM变换后的决策边界（这个部分实际上在二维图中无法直接展示变换后的效果，
# 因为变换是隐式的，此处省略，重点展示原始数据通过SVM分类的边界）
plt.subplot(1, 2, 2)
plt.scatter(X_scaled[y == 0, 0], X_scaled[y == 0, 1], color='lightblue')
plt.scatter(X_scaled[y == 1, 0], X_scaled[y == 1, 1], color='lightcoral')
plt.title('Data with Linear SVM Decision Boundary')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

# 同样的超平面绘制在此图上用于对比
plt.contour(XX, YY, Z, colors='gray', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.xlim(xlim)
plt.ylim(ylim)

plt.tight_layout()
plt.show()

结果：

我们可以看见生成的分类效果图，但这里的分类效果不好因为核函数选择的不完美需要不断尝试，这是支持向量机中最难的部分。

2. 多项式核（Polynomial Kernel）

多项式核通过将数据映射到更高维的特征空间来处理非线性关系。它模拟了数据点的多项式关系。

公式： $K(\mathbf{x}_i, \mathbf{x}_j) = (\gamma \mathbf{x}_i \cdot \mathbf{x}_j + r)^d$

其中 𝛾 是一个参数，控制映射的缩放；𝑟是偏置项，通常设为1；𝑑是多项式的度数。

举出实列：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_circles
from sklearn.svm import SVC
from sklearn.preprocessing import PolynomialFeatures

# 生成线性不可分的二维数据
X, y = make_circles(n_samples=100, factor=0.1, noise=0.1)
y = 2 * y - 1  # 调整标签为-1和1以便于后续SVM使用

# 映射到三维空间
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)

# 使用SVM（多项式核）对映射后的数据进行分类
svm = SVC(kernel='linear', C=1000)
svm.fit(X_poly, y)

# 分别绘制二维和三维图

# 二维图
plt.figure(figsize=(12, 6))

# 二维数据散点图
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='bwr', s=50, alpha=0.6)
plt.title('Original 2D Data (Non-linearly Separable)')
plt.xlabel('X1')
plt.ylabel('X2')
plt.axis('equal')
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)

# 三维图
ax = plt.subplot(1, 2, 2, projection='3d')

# 分类边界在三维空间中的近似表示（使用网格和分类预测）
xx, yy = np.meshgrid(np.linspace(-1.5, 1.5, 100), np.linspace(-1.5, 1.5, 100))
grid = np.vstack([xx.ravel(), yy.ravel()]).T
grid_poly = poly.transform(grid)
zz = svm.decision_function(grid_poly).reshape(xx.shape)

# 绘制三维散点图
ax.scatter3D(X_poly[y == 1, 0], X_poly[y == 1, 1], X_poly[y == 1, 2], c='tab:blue', marker='o', label='Class 1')
ax.scatter3D(X_poly[y == -1, 0], X_poly[y == -1, 1], X_poly[y == -1, 2], c='tab:red', marker='s', label='Class -1')

# 绘制决策边界（近似超平面）
ax.plot_surface(xx, yy, zz, alpha=0.3, cmap='gray_r', linewidth=0, antialiased=False)
ax.set_title('Projected to 3D with Polynomial Kernel (Linearly Separable)')
ax.set_xlabel('Polynomial Feature 1')
ax.set_ylabel('Polynomial Feature 2')
ax.set_zlabel('Polynomial Feature 3')
ax.view_init(elev=25, azim=-35)  # 设置视角

plt.tight_layout()
plt.show()

运行结果：

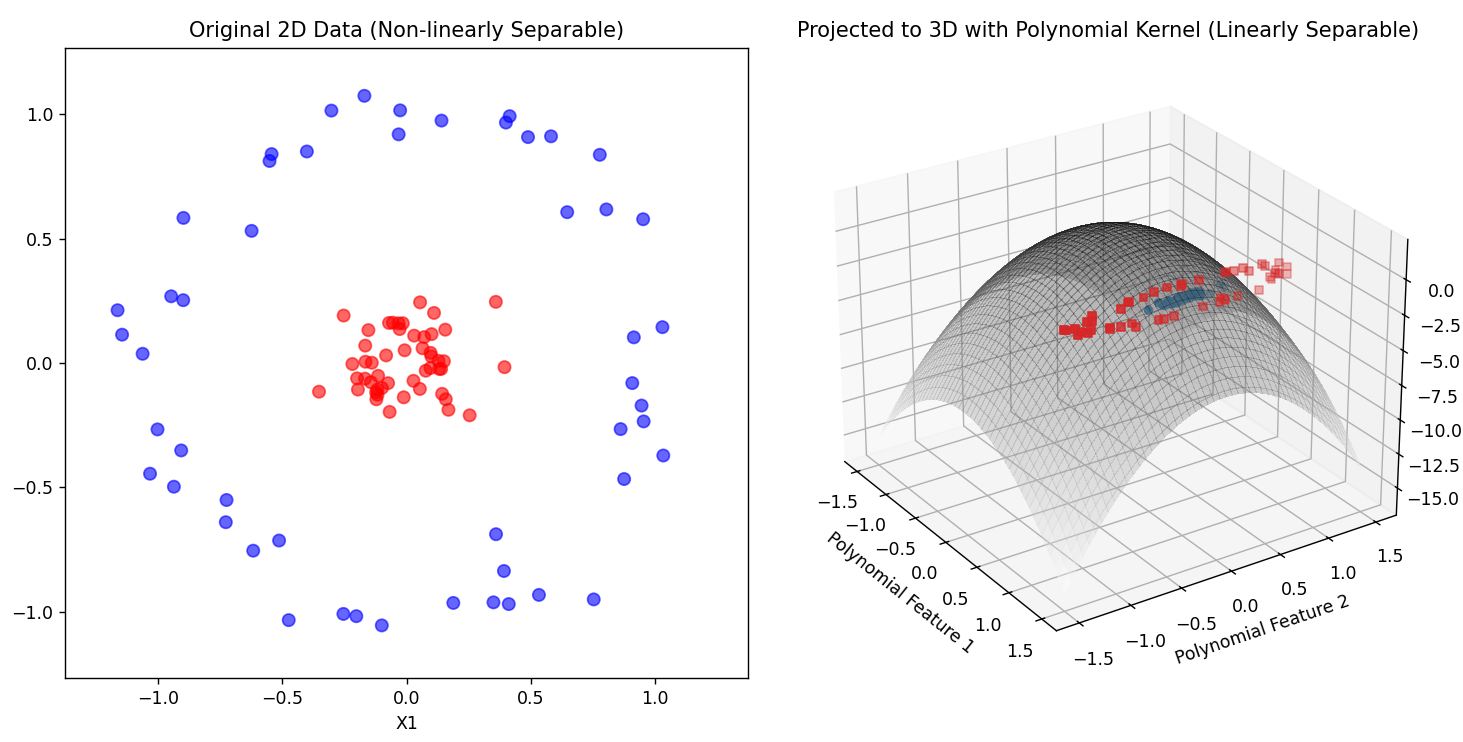
正如很多数据如此我们就是将其映射到高维空间中就可分了。

3. 径向基函数（RBF）核（Radial Basis Function Kernel）

RBF核，也称为高斯核，是最常用的核函数之一。它通过测量数据点之间的欧几里得距离来捕捉非线性关系。

公式： $K(\mathbf{x}_i, \mathbf{x}_j) = \exp\left(-\frac{||\mathbf{x}_i - \mathbf{x}_j||^2}{2\sigma^2}\right)$

其中 𝜎是核函数的宽度参数，控制了高斯分布的方差。

4. Sigmoid核

Sigmoid核类似于神经网络中的Sigmoid激活函数，它试图模拟数据点之间的逻辑关系。

公式： $K(\mathbf{x}_i, \mathbf{x}_j) = \tanh(\gamma \mathbf{x}_i \cdot \mathbf{x}_j + r)$

其中 𝛾和 𝑟 的含义与多项式核中相同。

SVM的优化问题

SVM的训练过程可以看作是一个凸优化问题。目标是找到一个解，这个解在满足所有训练样本正确分类的同时，最大化间隔。这通常通过求解一个二次规划问题来实现。

实际应用

SVM在许多领域都有应用，包括但不限于图像识别、文本分类、生物信息学和金融分析。其强大的泛化能力使得SVM成为许多实际问题的首选模型。

结论

支持向量机是一种强大的分类器，其通过核函数扩展到非线性问题的能力，使其在机器学习领域中具有独特的地位。这四个核函数是非常重要和常见的核函数，但映射到高维空间时并不是一定可以线性可分的。

参考文献

Vapnik, V. (2013). The Nature of Statistical Learning Theory. Springer Science & Business Media.
Hsu, C., Chang, C., & Lin, C. (2010). A practical guide to support vector classification. Technical report, Department of Computer Science, National Taiwan University.
传统机器学习(七)支持向量机(1)超平面、SVM硬间隔、软间隔模型和损失函数_软间隔支持向量几何理解-CSDN博客

01_6

关注

26
点赞
踩
29

收藏

觉得还不错? 一键收藏
1
评论
支持向量机及其核函数

在最简单的情况下，即数据是线性可分的，SVM的目标是找到一个超平面（淡蓝色的区域），它不仅能够正确分类数据，而且与最近的点（支持向量）之间的距离最大化（中间的实线）。支持向量机是一种强大的分类器，其通过核函数扩展到非线性问题的能力，使其在机器学习领域中具有独特的地位。软间隔SVM允许正支持平面的负侧有正样本，也允许负支持平面正侧有负样本，它的目标在于，尽量让两个支持面的距离更大的同时。我们可以看见生成的分类效果图，但这里的分类效果不好因为核函数选择的不完美需要不断尝试，这是支持向量机中最难的部分。
复制链接

扫一扫