Rectified Linear Unit (ReLU)

The Rectified Linear Unit (ReLU) computes the function $f(x)=max(0,x)$, which is simply thresholded at zero.

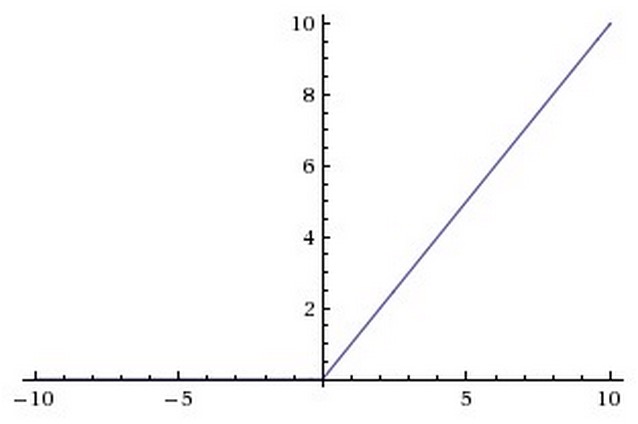
There are several pros and cons to using the ReLUs:

1. (Pros) Compared to sigmoid/tanh neurons that involve expensive operations (exponentials, etc.), the ReLU can be implemented by simply thresholding a matrix of activations at zero. Meanwhile, ReLUs does not suffer from saturating.
2. (Pros) It was found to greatly accelerate the convergence of stochastic gradient descent compared to the sigmoid/tanh functions. It is argued that this is due to its linear, non-saturating form.
3. (Cons) Unfortunately, ReLU units can be fragile during training and can “die”. For example, a large gradient flowing through a ReLU neuron could cause the weights to update in such a way that the neuron will never activate on any datapoint again. If this happens, then the gradient flowing through the unit will forever be zero from that point on. That is, the ReLU units can irreversibly die during training since they can get knocked off the data manifold. For example, you may find that as much as 40% of your network can be “dead” (i.e., neurons that never activate across the entire training dataset) if the learning rate is set too high. With a proper setting of the learning rate this is less frequently an issue.

Leaky ReLU

Leaky ReLUs are one attempt to fix the “dying ReLU” problem. Instead of the function being zero when $x<0$, a leaky ReLU will instead have a small negative slope(of 0.01, or so). That is, the function computes $f(x)=ax$ if $x<0$ and $f(x)=x$ if $x\geqslant 0$, where $a$ is a small constant. Some people report success with this form of activation function, but the results are not always consistent.

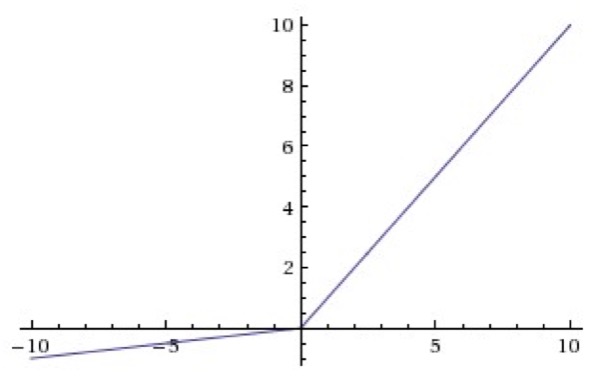
Parametric ReLU

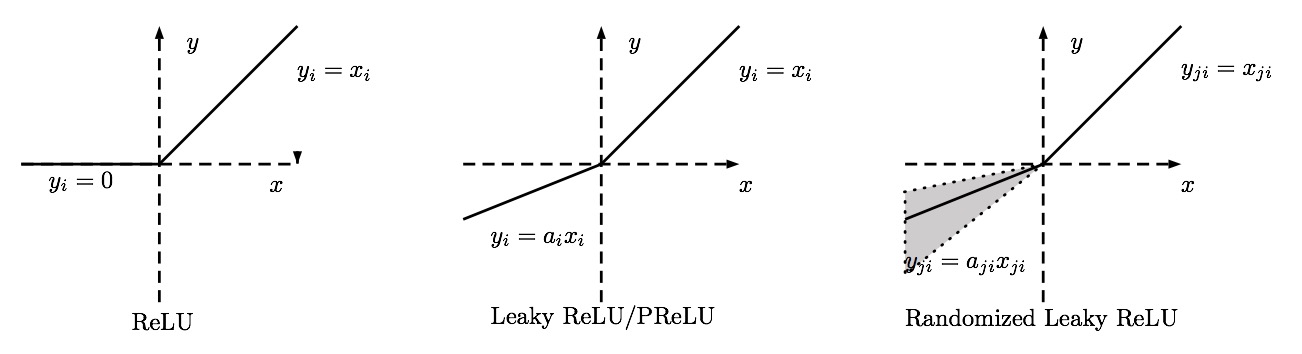
The first variant is called parametric rectified linear unit (PReLU). In PReLU, the slopes of negative part are learned from data rather than pre-defined.

Randomized ReLU

In RReLU, the slopes of negative parts are randomized in a given range in the training, and then fixed in the testing. As mentioned in [B. Xu, N. Wang, T. Chen, and M. Li. Empirical Evaluation of Rectified Activations in Convolution Network. In ICML Deep Learning Workshop, 2015.], in a recent Kaggle National Data Science Bowl (NDSB) competition, it is reported that RReLU could reduce overfitting due to its randomized nature. Moreover, suggested by the NDSB competition winner, the random $a_i$ in training is sampled from $1/U(3,8)$ and in test time it is fixed as its expectation, i.e., $2/(l+u)=2/11$.

In conclusion, three types of ReLU variants all consistently outperform the original ReLU in these three data sets. And PReLU and RReLU seem better choices.