在介绍双线性插值前,我们先介绍一下拉格朗日插值多项式。
拉格朗日插值法:
在数值分析中,拉格朗日插值法是以法国十八世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。许多实际问题中都用函数来表示某种内在联系或规律,而不少函数都只能通过实验和观测来了解。如对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。这样的多项式称为拉格朗日(插值)多项式。数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。拉格朗日插值法最早被英国数学家爱德华·华林于1779年发现[1],不久后(1783年)由莱昂哈德·欧拉再次发现。1795年,拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法,从此他的名字就和这个方法联系在一起[2]。
对于给定的若n+1个点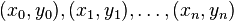 ,对应于它们的次数不超过n的拉格朗日多项式
,对应于它们的次数不超过n的拉格朗日多项式 只有一个。如果计入次数更高的多项式,则有无穷个,因为所有与
只有一个。如果计入次数更高的多项式,则有无穷个,因为所有与 相差
相差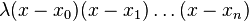 的多项式都满足条件。例子:
的多项式都满足条件。例子:

以及
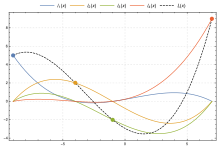
 各穿过对应的一点,并在其它的三个点的
x值上取零。
各穿过对应的一点,并在其它的三个点的
x值上取零。
定义
对某个多项式函数,已知有给定的k + 1个取值点:
其中 对应着自变量的位置,而
对应着自变量的位置,而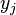 对应着函数在这个位置的取值。
对应着函数在这个位置的取值。
假设任意两个不同的xj都互不相同,那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为:
其中每个 为拉格朗日基本多项式(或称插值基函数),其表达式为:
为拉格朗日基本多项式(或称插值基函数),其表达式为:
拉格朗日基本多项式 的特点是在
的特点是在 上取值为1,在其它的点
上取值为1,在其它的点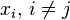 上取值为0。
上取值为0。
范例
假设有某个二次多项式函数 ,已知它在三个点上的取值为:
,已知它在三个点上的取值为:
要求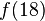 的值。
的值。
首先写出每个拉格朗日基本多项式:
然后应用拉格朗日插值法,就可以得到 的表达式(
的表达式( 为函数
为函数 的插值函数):
的插值函数):
此时代入数值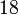 就可以求出所需之值:
就可以求出所需之值: 。
。
证明
存在性
对于给定的k+1个点: ,拉格朗日插值法的思路是找到一个在一点
,拉格朗日插值法的思路是找到一个在一点 取值为1,而在其他点取值都是0的多项式
取值为1,而在其他点取值都是0的多项式 。这样,多项式
。这样,多项式 在点
在点 取值为
取值为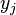 ,而在其他点取值都是0。而多项式
,而在其他点取值都是0。而多项式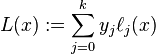 就可以满足
就可以满足
在其它点取值为0的多项式容易找到,例如:
它在点 取值为:
取值为: 。由于已经假定
。由于已经假定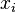 两两互不相同,因此上面的取值不等于0。于是,将多项式除以这个取值,就得到一个满足“在
两两互不相同,因此上面的取值不等于0。于是,将多项式除以这个取值,就得到一个满足“在 取值为1,而在其他点取值都是0的多项式”:
取值为1,而在其他点取值都是0的多项式”:
这就是拉格朗日基本多项式。
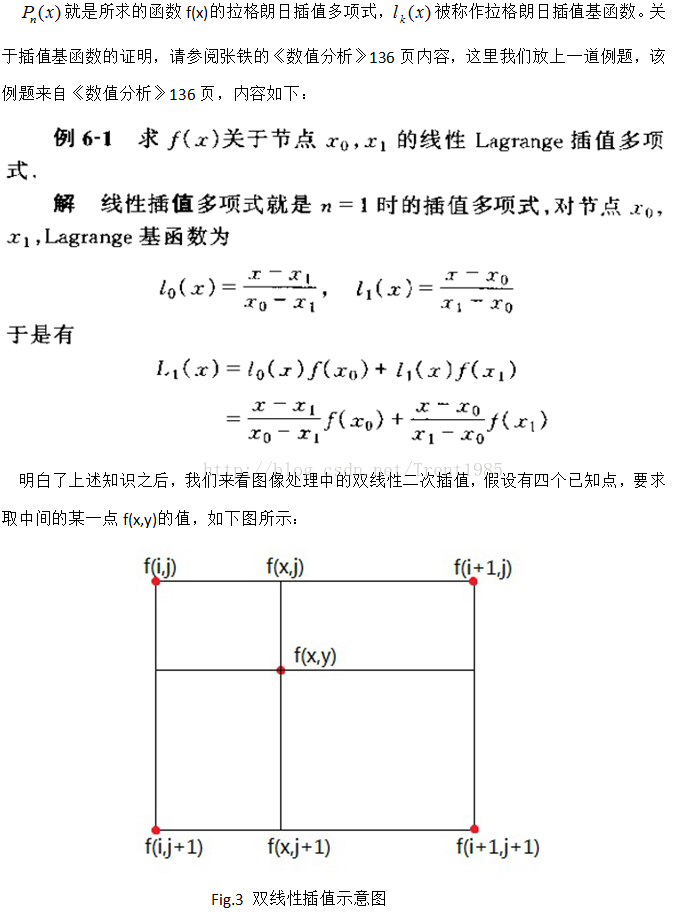
我们的方法是这样的,根据水平方向上的双线性二次插值,由f(I,j)和f(i+1,j)求取f(x,j),由
f(I,j+1)和f(i+1,j+1)求取f(x,j+1),然后再根据这两点的二次插值求取f(x,y)。
根据前面的例题,我们可以很容易的求取各点插值如下:
f(x,j)=(i+1-x)f(I,j)+(x-i)f(i+1,j) 公式1-(4)
f(x,j+1)=(i+1-x)f(I,j+1)+(x-i)f(i+1,j+1) 公式1-(5)
f(x,y)=(i+1-y)f(x,j)+(y-j)f(x,j+1) 公式1-(6)
以上三式综合可以得到:
f(x,y)=(j+1-y)(i+1-x)f(I,j)+(j+1-y)(x-i)f(i+1,j)+(y-j)(i+1-x)f(I,j+1)+(y-j)(x-i)f(i+1,j+1) 公式1-(7)
我们令x=i+p,y=j+q得:
f(i+p,j+q)=(1-q)(1-p)f(I,j)+p(1-q)f(i+1,j)+q(1-p)f(I,j+1)+pqf(i+1,j+1) 公式1-(8)
上式即为数字图像处理中的双线性二次插值公式。
参考博客:https://www.cnblogs.com/ECJTUACM-873284962/p/6833391.htmlhttp://blog.csdn.net/trent1985/article/details/45150677










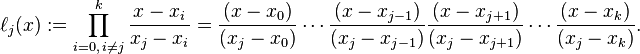

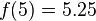
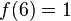
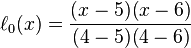
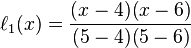

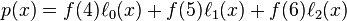
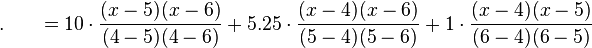
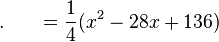
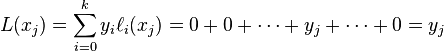
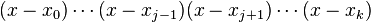
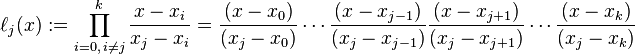













 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








